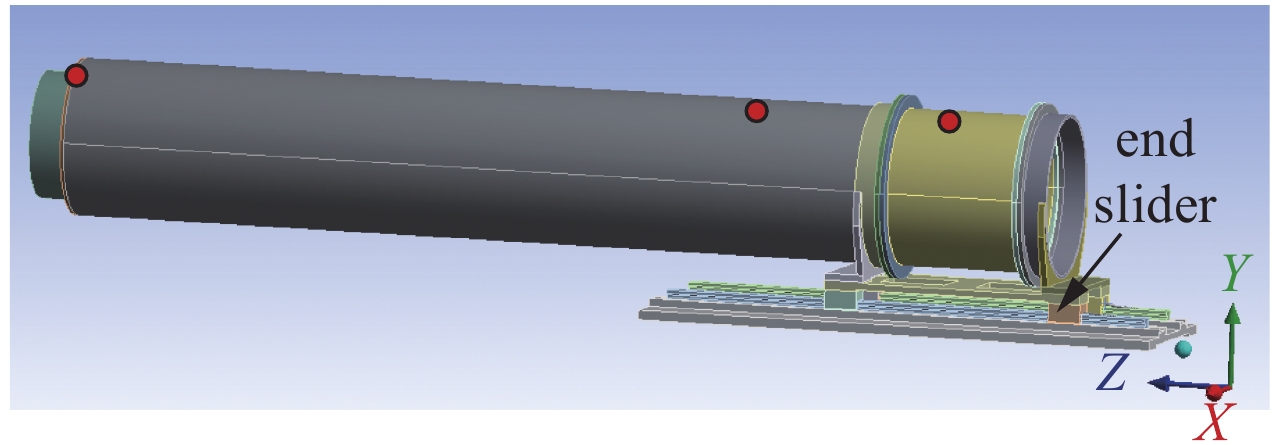
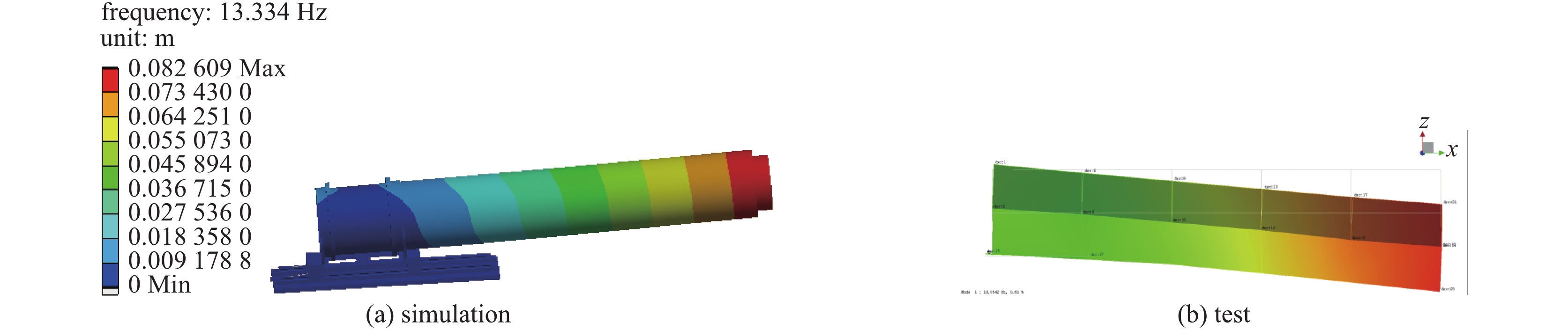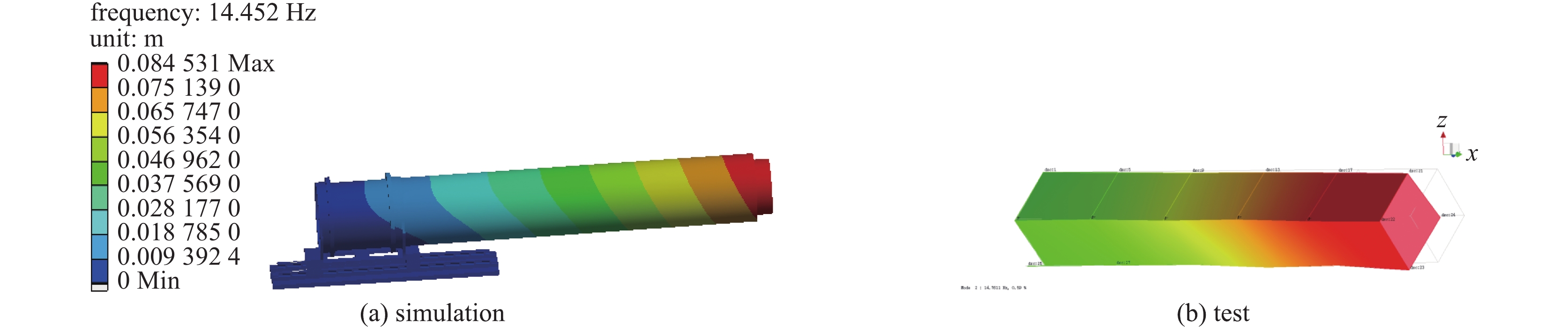Dynamic modeling on a linear rolling guide based on thin layer element and spring element
-
摘要: 针对某大型光机装置中使用的LM型直线导轨-滑块的结合面,采用薄层单元与弹簧单元模拟其接触面,建立了大行程传输结构模拟件的有限元模型。通过模型修正方法,根据模态试验结果对薄层单元弹性模量以及弹簧刚度进行了识别。模型修正后,结构前三阶模态频率计算结果与试验结果最大差别为2.23%,地脉动载荷下各测点位移响应计算结果与试验结果最大差别为7.61%。计算结果与试验结果具有较好的一致性,验证了模型的有效性。Abstract: The guide-slider joint of the transmission mechanism with a long stroke has a great effect on the dynamic characteristic of the structure. Aiming at the dynamic modeling on the joint part of the LM linear rolling guide in some large laser facility, the finite element (FE) model of the transmission mechanism with a long stroke is established based on the thin layer element and spring element. The modulus of the thin element and the stiffness of the spring element are identified by the model updating method and the modal experimental results. After the model update, the maximal error of the first three modal frequencies between simulation and experiment is 2.29%, and the maximal error of the point’s displacement response between simulation and experiment is 7.61% under the ambient vibration. The results of simulation and experiment are consistent, which shows that the model is effective and reasonable. The study provides a theoretical basis for the high confidence dynamic modeling on other structure with such a the joint.
-
Key words:
- linear rolling guide /
- dynamic modeling /
- thin layer element /
- spring element /
- parameter identification
-
表 1 大行程传输机构模拟件模态试验结果
Table 1. Modal experimental results of the transmission mechanism with a long stroke
rank frequency/Hz modal damping ratio/% modal shape 1 13.05 0.54 vertical rocking 2 14.78 0.66 horizontal rocking 3 24.20 18.87 translating along with the guide 表 2 微振动测试结果
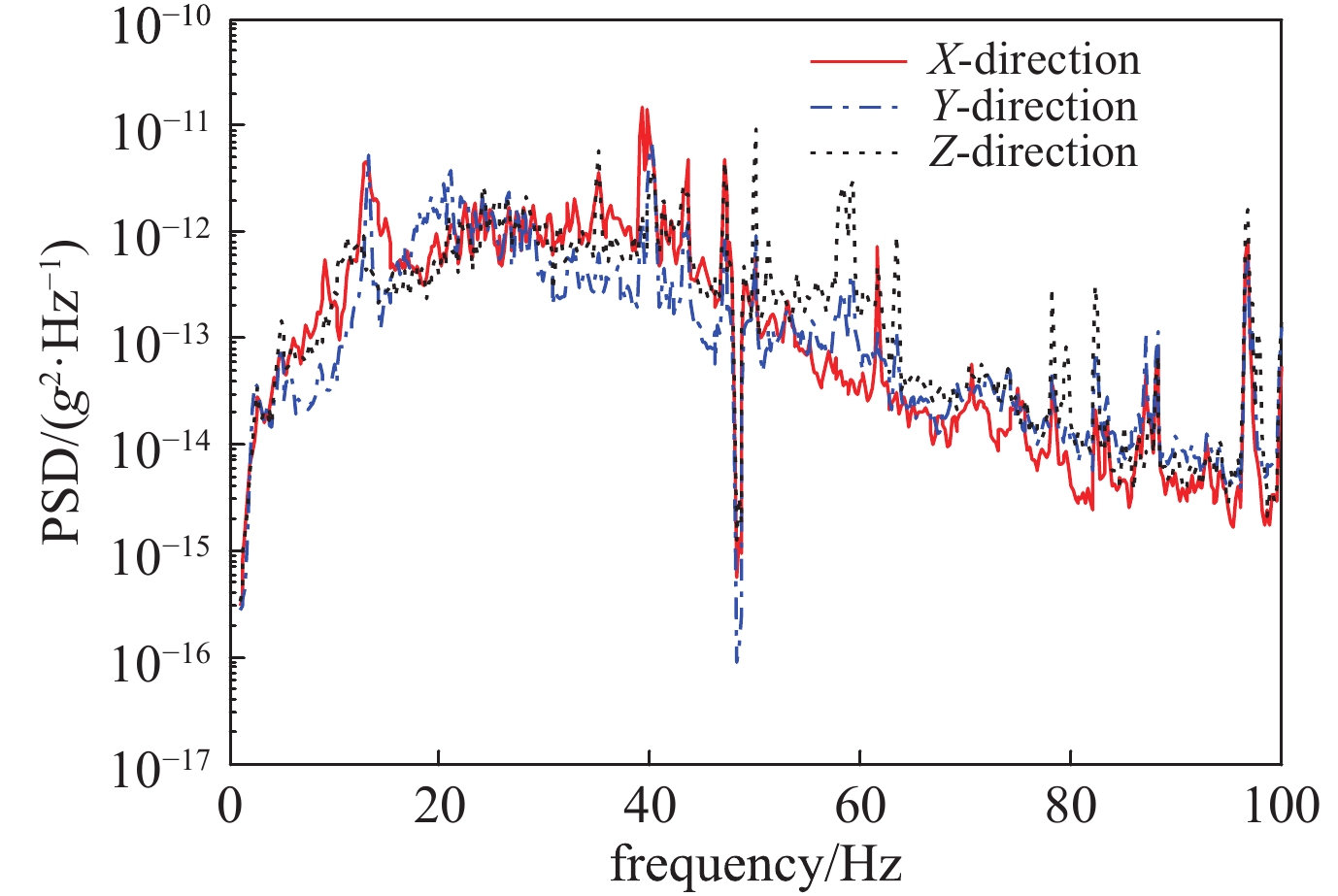
Table 2. Results on the micro-vibration experiment
measured point No. 1 2 3 4 5 displacement/10−2μm 1.84 2.06 2.69 3.56 13.01 表 3 结构前三阶模态频率计算结果与试验结果比较
Table 3. Comparison on the first three natural frequencies between simulation and experiment
rank experimental result/Hz initial result/Hz error/% updated result/Hz error/% 1 13.05 16.92 29.63 13.33 2.15 2 14.78 17.42 17.86 14.45 −2.23 3 24.20 18.49 −23.60 24.28 0.33 表 4 测点合位移计算结果与试验结果比较
Table 4. Comparison on the resultant displacement between simulation and experiment
measured point
No.experimental result/
10−2μmsimulating result/
10−2μmerror/% 1 1.84 1.98 7.61 2 2.06 2.08 0.97 3 2.69 2.62 −2.60 4 3.56 3.59 0.84 5 13.01 13.91 6.92 -
[1] 屈重年, 伍良生, 肖毅川, 等. 机床导轨技术研究综述[J]. 制造技术与机床, 2012(1):31-36. (Qu Chongnian, Wu Liangsheng, Xiao Yichuan, et al. Summary of guide way technology research on machine tools[J]. Manufacturing Technology & Machine Tool, 2012(1): 31-36 [2] Zhang G P, Huang Y M, Shi W H, et al. Predicting dynamic behaviors of a whole machine tool structure based on computer-aided engineering[J]. International Journal of Machine Tools and Manufacture, 2003, 43(7): 699-706. doi: 10.1016/S0890-6955(03)00026-9 [3] Wu J S S, Chang J C, Hung J P. The effect of contact interface on dynamic characteristics of composite structures[J]. Mathematics and Computers in Simulation, 2007, 74(6): 454-467. doi: 10.1016/j.matcom.2006.07.003 [4] Wu J S S, Chang J C, Tsai G A, et al. The effect of bending loads on the dynamic behaviors of a rolling guide[J]. Journal of Mechanical Science and Technology, 2012, 26(3): 671-680. doi: 10.1007/s12206-011-1228-8 [5] Hung J P. Load effect on the vibration characteristics of a stage with rolling guides[J]. Journal of Mechanical Science and Technology, 2009, 23(1): 89-99. doi: 10.1007/s12206-008-0925-4 [6] 蒋书运, 祝书龙. 带滚珠丝杠副的直线导轨结合部动态刚度特性[J]. 机械工程学报, 2010, 46(1):92-99. (Jiang Shuyun, Zhu Shulong. Dynamic characteristic parameters of linear guide way joint with ball screw[J]. Journal of Mechanical Engineering, 2010, 46(1): 92-99 doi: 10.3901/JME.2010.01.092 [7] 孙伟, 孔祥希, 汪博, 等. 直线滚动导轨的 Hertz 接触建模及接触刚度的理论求解[J]. 工程力学, 2013, 30(7):230-234. (Sun Wei, Kong Xiangxi, Wang Bo, et al. Contact modeling and analytical solution of contact stiffness by Hertz theory for the linear rolling guide system[J]. Engineering Mechanics, 2013, 30(7): 230-234 [8] 王民, 乐兵兵, 裴二阳. 基于Hertz 接触的滚珠直线导轨副接触刚度建模与分析[J]. 北京工业大学学报, 2015, 41(8):1128-1133. (Wang Min, Le Bingbing, Pei Eryang. Contact stiffness modeling and analysis of linear ball guides based on Hertz contact theory[J]. Journal of Beijing University of Technology, 2015, 41(8): 1128-1133 [9] 张巍, 王民, 孙乐乐. 考虑预紧力和接触角变化的直线滚动导轨副刚度建模与分析[J]. 北京工业大学学报, 2018, 44(1):56-63. (Zhang Wei, Wang Min, Sun Lele. Stiffness modeling and analysis considering influences of preload and contact angle of a linear rolling guide[J]. Journal of Beijing University of Technology, 2018, 44(1): 56-63 [10] Wang J H. Experimental identification of mechanical joint parameters[J]. Journal of Vibration and Acoustics, 1991, 113: 28-36. doi: 10.1115/1.2930151 [11] Ohta H, Hayashi E. Vibration of linear guide way type recirculating linear ball bearing[J]. Journal of Sound and Vibration, 2000, 235(5): 847-861. doi: 10.1006/jsvi.2000.2950 [12] 张宇, 廖伯瑜. 机床结合部参数的有效识别方法[J]. 昆明理工大学学报, 1998, 23(2):36-41. (Zhang Yu, Liao Boyu. The efficient identification method of joint parameters of machine tools[J]. Journal of Kunming University of Science and Technology, 1998, 23(2): 36-41 [13] 毛宽民, 邢满禧, 李斌, 等. 滚动直线导轨副可动结合部动力学建模[J]. 华中科技大学学报:自然科学版, 2016, 44(7):81-85. (Mao Kuanmin, Xing Manxi, Li Bin, et al. Dynamic modeling for movable joint of rolling linear guide[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2016, 44(7): 81-85 [14] 田红亮, 刘芙蓉, 方子帆, 等. 引入各向同性虚拟材料的固定结合部模型[J]. 振动工程学报, 2013, 26(4):561-573. (Tian Hongliang, Liu Furong, Fang Zifan, et al. Immovable joint surface’s model using isotropic virtual material[J]. Journal of Vibration Engineering, 2013, 26(4): 561-573 doi: 10.3969/j.issn.1004-4523.2013.04.013 [15] 张学良, 范世荣, 温淑花, 等. 基于等效横观各向同性虚拟材料的固定结合部建模方法[J]. 机械工程学报, 2017, 53(15):141-147. (Zhang Xueliang, Fan Shirong, Wen Shuhua, et al. Modeling method of fixed joint interfaces equivalent transversely isotropic virtual material[J]. Journal of Mechanical Engineering, 2017, 53(15): 141-147 doi: 10.3901/JME.2017.15.141 [16] Tabatabaie M, Sommer S C. Analysis of soil-structure interaction due to ambient vibration[R]. UCRL-JC-130342, 1998. [17] 陈学前, 徐元利. 柔性基础对ICF装置稳定性的影响[J]. 强激光与粒子束, 2011, 23(6):1569-1573. (Chen Xueqian, Xu Yuanli. Studying on the influence of flexible foundation on the stability of ICF facility[J]. High Power Laser and Particle Beams, 2011, 23(6): 1569-1573 doi: 10.3788/HPLPB20112306.1569 -





 下载:
下载: