Structure coefficient in magnetically driven flyer plate experiment
-
摘要: 为了确定磁驱动飞片发射实验结构系数的范围、影响因素、结构系数与影响因素的关系,对聚龙一号装置上的磁驱动飞片发射实验进行了数值模拟和分析。数值模拟表明,磁流体力学程序能正确模拟聚龙一号装置上各个磁驱动飞片发射实验;磁驱动双侧飞片发射实验的结构系数为0.7~0.8;磁驱动单侧飞片发射实验的结构系数为0.80~0.85。磁驱动飞片发射实验的结构系数与实验加载电流无关,仅由磁驱动飞片发射实验的负载结构决定。磁驱动飞片发射实验的结构系数取决于阴阳电极极板的初始宽度、阴阳电极之间的初始间隙以及阴阳电极上飞片厚度之和等三个因素。在磁驱动飞片发射实验中,电极初始宽度、阴阳电极之间的初始间隙不变的情况下,结构系数由阴阳电极上飞片厚度之和确定,阴阳电极上飞片厚度之和越大,结构系数越大。Abstract: To determine the range and the influence factor of structure coefficient and, the relation between structure coefficient and influence factor, numerical simulations and analysis of magnetically driven flyer plate experiments on PTS facility are carried out. The numerical simulations show that the magneto-hydrodynamic code can correctly simulate each magnetically driven flyer plate experiment on PTS facility. The structure coefficient of magnetically driven two-sided flyer plate experiment is about 0.7−0.8 and the structure coefficient of one-sided experiment is about 0.80−0.85. The structure coefficient is independent of the measured experimental current, and only determined by the initial structure of experiment load. The structure coefficient is related to the initial widths of anode and cathode, the initial gap between anode and cathode, and the sum of depths of flyer plates on anode and cathode. When the initial widths of anode and cathode and the initial gap between anode and cathode are fixed, the greater sum depths of flyer plates on anode and cathode, the greater the structure coefficient of magnetically driven flyer plate experiment.
-
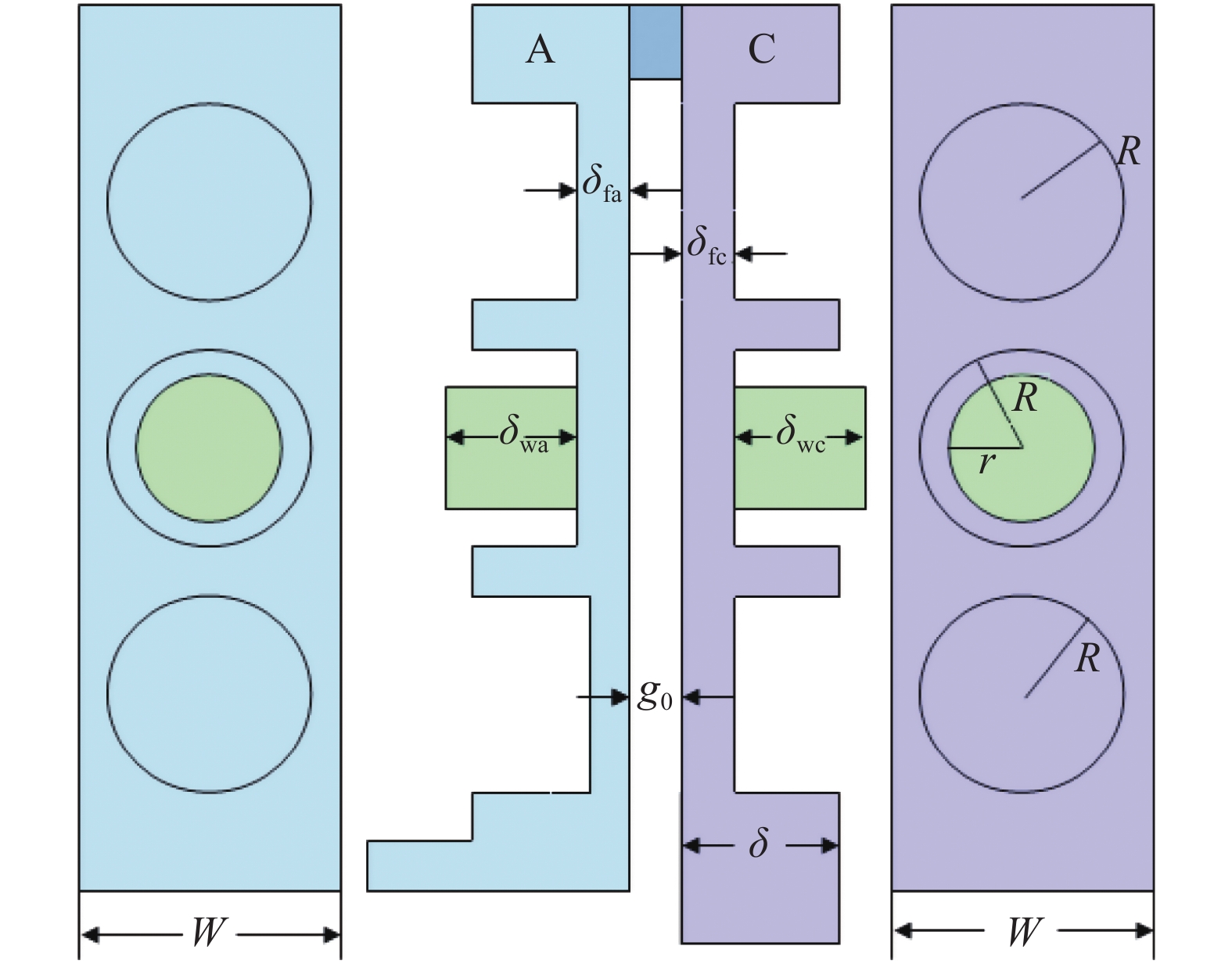
表 1 聚龙一号装置上磁驱动飞片发射实验的负载参数
Table 1. Load parameters for magnetically driven flyer plate launch experiments on PTS facility
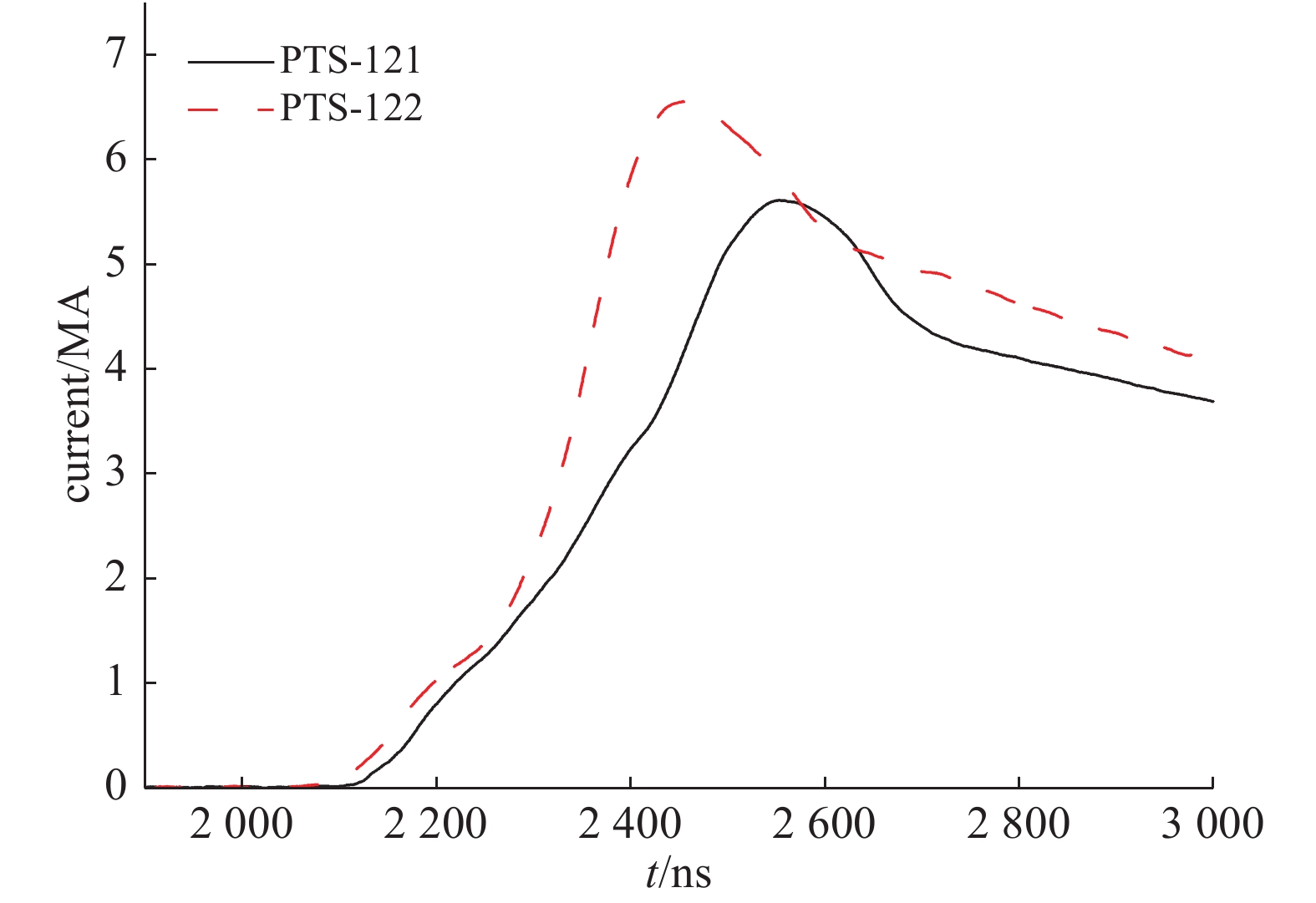
experiment name ${\delta _{{\rm{fa}}}}$/mm ${\delta _{{\rm{wa}}}}$/mm ${\delta _{{\rm{fc}}}}$/mm ${\delta _{{\rm{wc}}}}$/mm ${g_0}$/mm W/mm PTS-061 0.972 − 5 − 2 15 PTS-064 1.041 − 5 − 1.2 12.5 PTS-120top 1.047 − 0.986 − 1.2 9 PTS-120middle 1.067 5 1.299 5 1.2 9 PTS-120top 1.041 − 1.016 − 1.2 9 PTS-121top 1.401 − 1.076 − 1.2 9 PTS-121middle 1.120 5 1.276 5 1.2 9 PTS-121bottom 0.930 − 1.570 − 1.2 9 PTS-122top 1.459 − 1.089 − 1.2 9 PTS-122middle 1.171 5 1.281 5 1.2 9 PTS-122bottom 0.960 − 1.570 − 1.2 9 表 2 聚龙一号装置上磁驱动飞片发射实验的结构系数
Table 2. Structure coefficients for magnetically driven flyer plate launch experiments on PTS facility
experiment name ${g_0}$/mm W/mm (${\delta _{{\rm{fa}}}}$+${\delta _{{\rm{fc}}}}$)/mm f PTS-061 2 15 5.972 0.83 PTS-064 1.2 12.5 6.041 0.81 PTS-120top 1.2 9 2.033 0.705 PTS-121bottom 1.2 9 2.50 0.75 PTS-122top 1.2 9 2.548 0.78 PTS-122bottom 1.2 9 2.53 0.75 -
[1] Knudson M D, Lemke R W, Hayes D B, et al. Near-absolute Hugoniot measurements in aluminum to 500 GPa using a magnetically accelerated flyer plate technique[J]. Journal of Applied Physics, 2003, 94(7): 4420-4431. doi: 10.1063/1.1604967 [2] Lemke R W, Knudson M D, Bliss D E, et al. Magnetically accelerated, ultrahigh velocity flyer plates for shock wave experiments[J]. Journal of Applied Physics, 2005, 98: 073530. doi: 10.1063/1.2084316 [3] Lemke R W, Knudson M D, Davis J P. Magnetically driven hyper-velocity launch capability at the Sandia Z accelerator[J]. International Journal of Impact Engineering, 2011, 38(6): 480-485. doi: 10.1016/j.ijimpeng.2010.10.019 [4] Knudson M D, Hanson D L, Bailey J E, et al. Equation of state measurements in liquid deuterium to 70 GPa[J]. Physical Review Letters, 2001, 87: 225501. doi: 10.1103/PhysRevLett.87.225501 [5] Knudson M D, Hanson D L, Bailey J E, et al. Use of a wave reverberation technique to infer the density compression of shocked liquid deuterium to 75 GPa[J]. Physical Review Letters, 2003, 90: 035505. doi: 10.1103/PhysRevLett.90.035505 [6] Knudson M D, Hanson D L, Bailey J E, et al. Principal Hugoniot, reverberating wave, and mechanical reshock measurements of liquid deuterium to 400 GPa using plate impact techniques[J]. Physical Review B, 2004, 69: 144209. doi: 10.1103/PhysRevB.69.144209 [7] Reisman D B, Toor A, Cauble R C. Magnetically driven isentropic compression experiments on the Z accelerator[J]. Journal of Applied Physics, 2001, 89(3): 1625-1633. doi: 10.1063/1.1337082 [8] Lemke R W, Knudson M D, Hall C A, et al. Characterization of magnetically accelerated flyer plates[J]. Physics of Plasmas, 2003, 10(4): 1092-1099. doi: 10.1063/1.1554740 [9] Davis J P, Brown J L, Knudson M D, et al. Analysis of shockless dynamic compression data on solids to multimegabar pressure: application to tantalum[J]. Journal of Applied Physics, 2014, 116: 204903. doi: 10.1063/1.4902863 [10] Kan Mingxian, Zhang Zhaohui, Xiao Bo, et al. Simulation of magnetically driven flyer plate experiments with an improved magnetic field boundary formula[J]. High Energy Density Physics, 2018, 26: 38-43. doi: 10.1016/j.hedp.2017.12.002 [11] 阚明先, 王刚华, 肖波, 等. 磁驱动单侧飞片实验的数值模拟研究[J]. 爆炸与冲击, 2020, 40:033304. (Kan Mingxian, Wang Ganghua, Xiao Bo, et al. Simulation study of magnetically driven one-sided flyer plate experiment[J]. Explosion and Shock Waves, 2020, 40: 033304 doi: 10.11883/bzycj-2019-0103 [12] Deng Jianjun, Xie Weiping, Feng Shuping, et al. Initial performance of the Primary Test Stand[J]. IEEE TPS, 2013, 41(10): 2580-2583. [13] 杨龙, 王刚华, 阚明先, 等. 基于MDSC程序的Z箍缩内爆单温和三温模拟分析[J]. 高压物理学报, 2016, 30(1):64-70. (Yang Long, Wang Ganghua, Kan Mingxian, et al. A numerical simulation analysis of mono-temperature and tri-temperature models by MDSC program in Z-pinch implosion[J]. Chinese Journal of High Pressure Physics, 2016, 30(1): 64-70 doi: 10.11858/gywlxb.2016.01.010 [14] 阚明先, 张朝辉, 段书超, 等. “聚龙一号”装置上磁驱动铝飞片实验的数值模拟[J]. 强激光与粒子束, 2015, 27:125001. (Kan Mingxian, Zhang Zhaohui, Duan Shuchao, et al. Numerical simulation of magnetically driven aluminum flyer plate on PTS accelerator[J]. High Power Laser and Particle Beams, 2015, 27: 125001 doi: 10.11884/HPLPB201527.125001 [15] 王贵林, 张朝辉, 郭帅, 等. 聚龙一号装置上铜的准等熵压缩线实验测量研究[J]. 强激光与粒子束, 2016, 28:055010. (Wang Guilin, Zhang Zhaohui, Guo Shuai, et al. Experimental measured of quasi-isentrope for copper on PTS[J]. High Power Laser and Particle Beams, 2016, 28: 055010 doi: 10.11884/HPLPB201628.055010 [16] 阚明先, 杨龙, 段书超, 等. 聚龙一号装置上磁驱动铝飞片发射实验的数值分析与再设计[J]. 爆炸与冲击, 2017, 37(5):793-798. (Kan Mingxian, Yang Long, Duan Shuchao, et al. Numerical analysis and design of magnetically driven aluminum flyer plate on PTS accelerator[J]. Explosion and Shock Waves, 2017, 37(5): 793-798 doi: 10.11883/1001-1455(2017)05-0793-06 [17] 阚明先, 蒋吉昊, 王刚华, 等. 套筒内爆ALE方法二维MHD数值模拟[J]. 四川大学学报, 2007, 44(1):91-96. (Kan Mingxian, Jiang Jihao, Wang Ganghua, et al. ALE simulation 2D MHD for liner[J]. Journal of Sichuan University, 2007, 44(1): 91-96 [18] 阚明先, 王刚华, 赵海龙, 等. 磁驱动飞片二维磁流体力学数值模拟[J]. 强激光与粒子束, 2013, 25(8):2137-2141. (Kan Mingxian, Wang Ganghua, Zhao Hailong, et al. Two dimensional magneto-hydrodynamic simulations of magnetically accelerated flyer plates[J]. High Power Laser and Particle Beams, 2013, 25(8): 2137-2141 doi: 10.3788/HPLPB20132508.2137 [19] 阚明先, 王刚华, 肖波, 等. 二维弹塑性磁流体力学数值模拟[J]. 强激光与粒子束, 2018, 30:065002. (Kan Mingxian, Wang Ganghua, Xiao Bo, et al. Two dimensional elasto-plastic MHD numerical simulation[J]. High Power Laser and Particle Beams, 2018, 30: 065002 doi: 10.11884/HPLPB201830.170306 [20] 阚明先, 段书超, 张朝辉, 等. 二维磁驱动数值模拟程序MDSC2的验证与确认[J]. 强激光与粒子束, 2019, 31:065001. (Kan Mingxian, Duan Shuchao, Zhang Zhaohui, et al. Verification and validation of two dimensional magnetically driven simulation code MDSC2[J]. High Power Laser and Particle Beams, 2019, 31: 065001 doi: 10.11884/HPLPB201931.180300 [21] 阚明先, 王刚华, 赵海龙, 等. 金属电阻率模型[J]. 爆炸与冲击, 2013, 33(3):282-286. (Kan Mingxian, Wang Ganghua, Zhao Hailong, et al. Electrical resistivity model for metals[J]. Explosion and shock waves, 2013, 33(3): 282-286 doi: 10.3969/j.issn.1001-1455.2013.03.010 -




 下载:
下载: