Research progress of low-temporal-coherence light frequency conversion technology for high power Nd:glass laser system
-
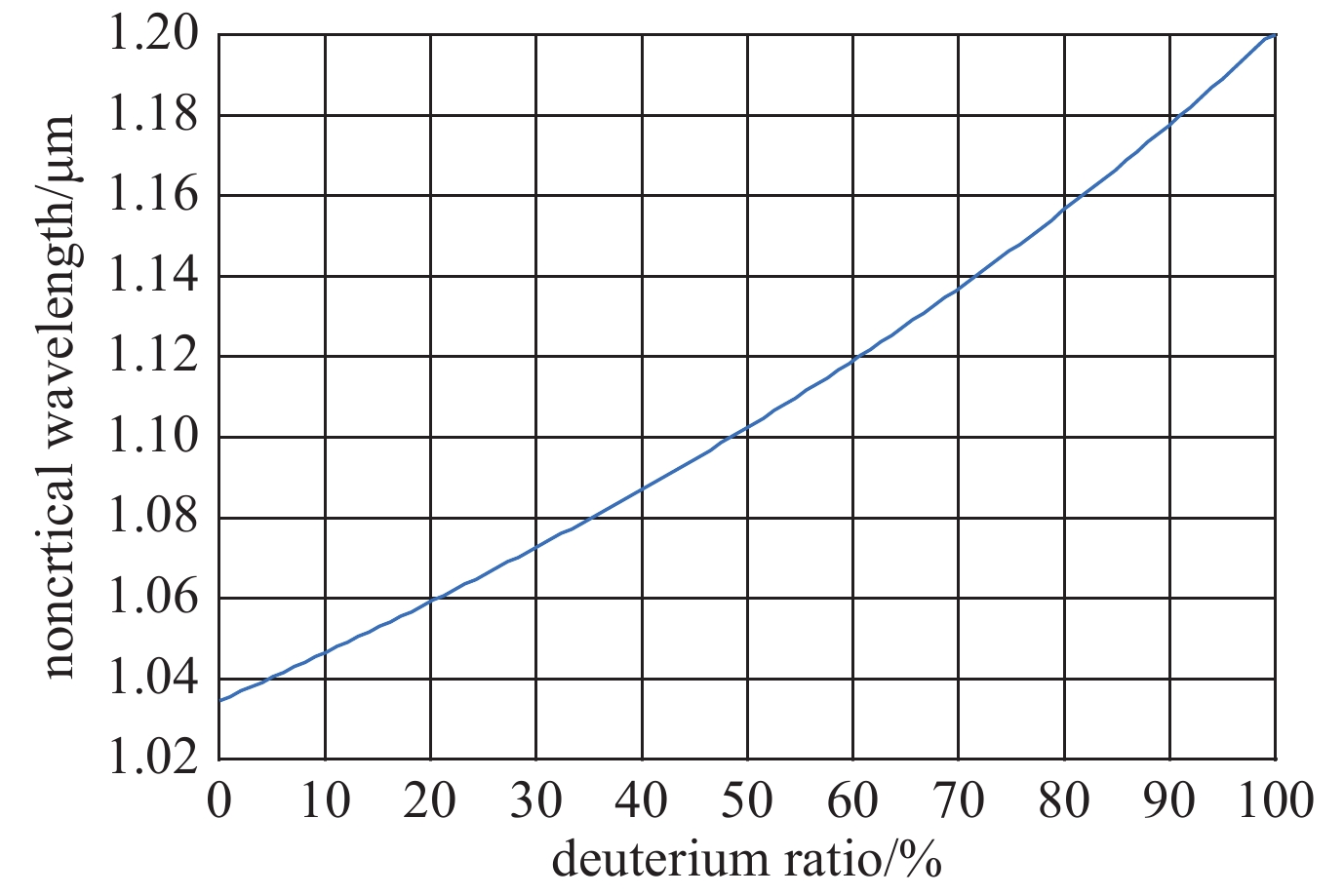
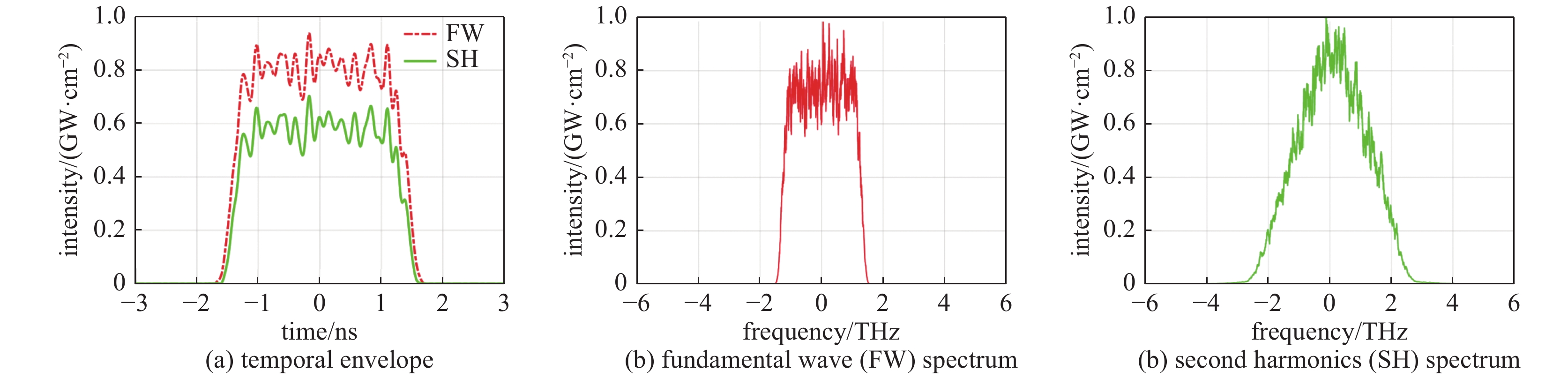
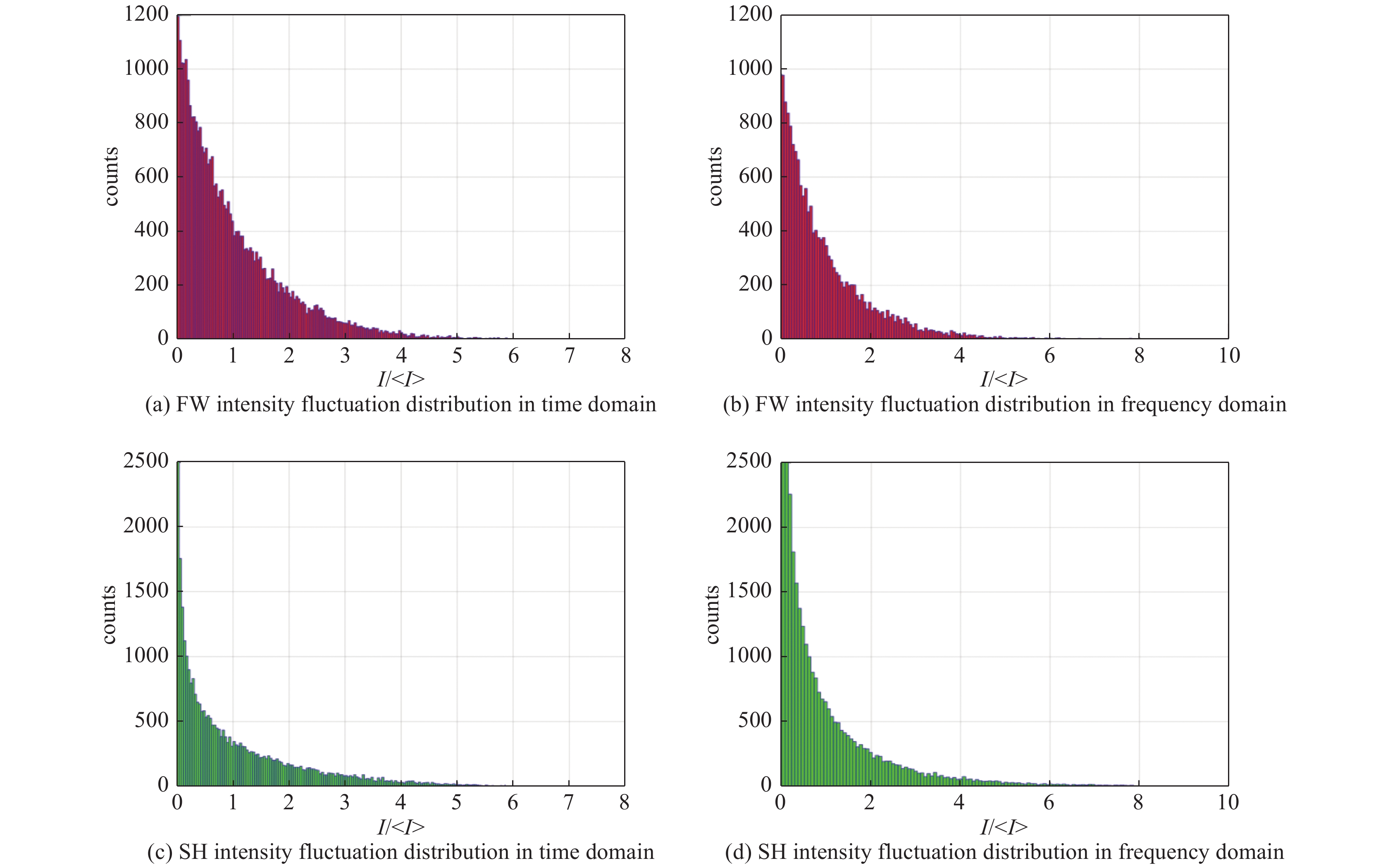
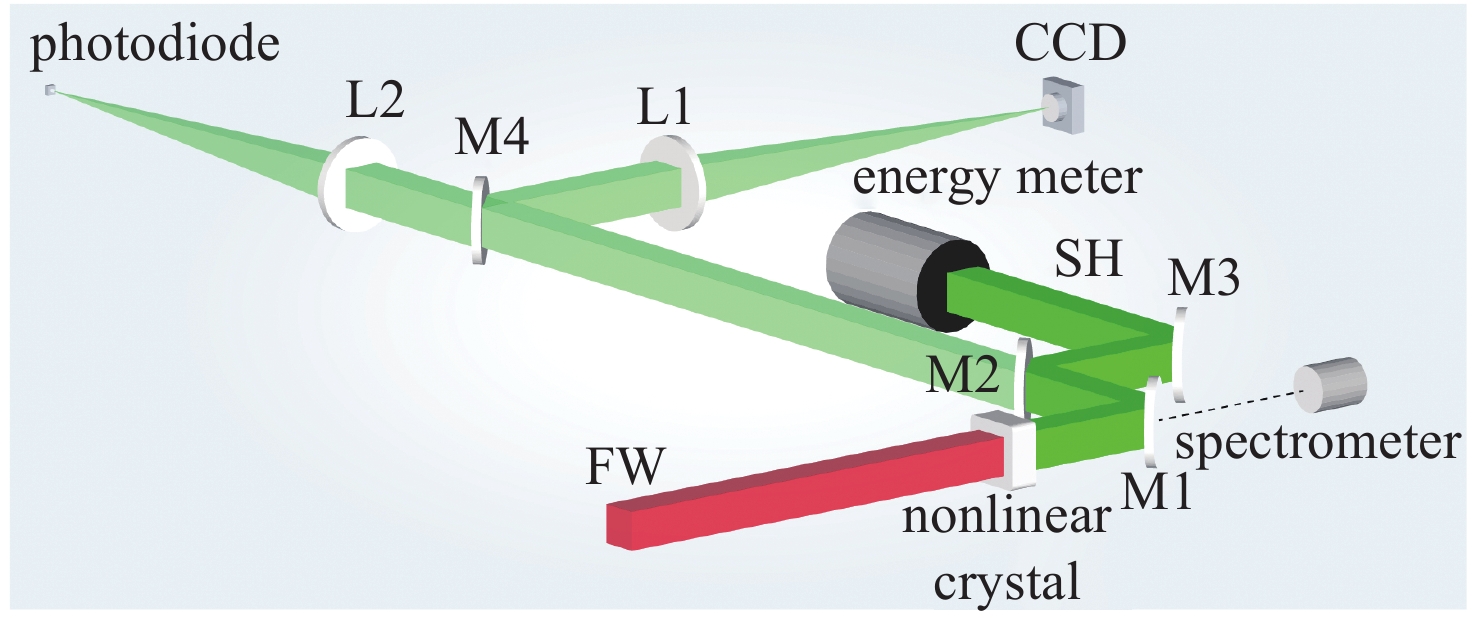
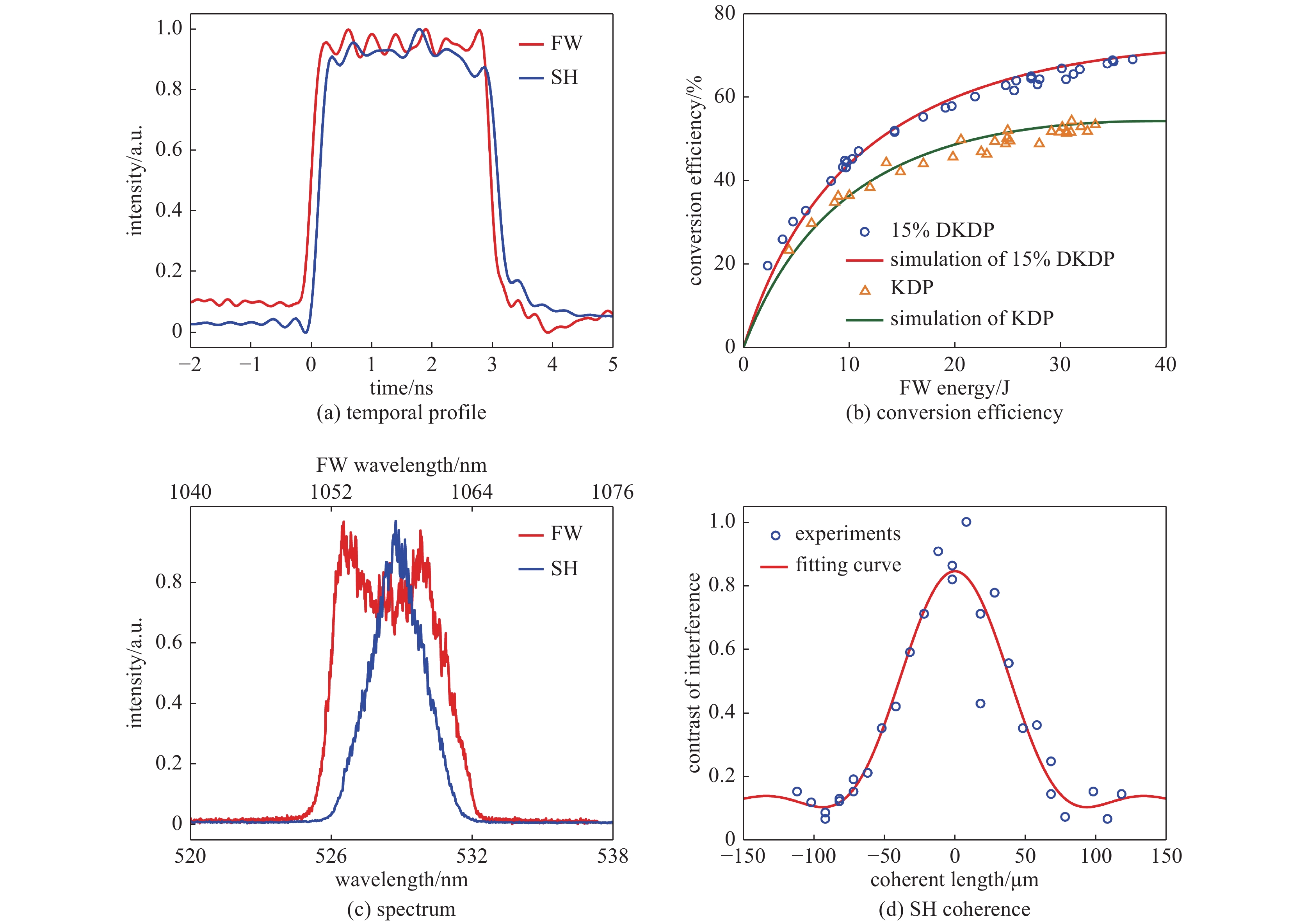
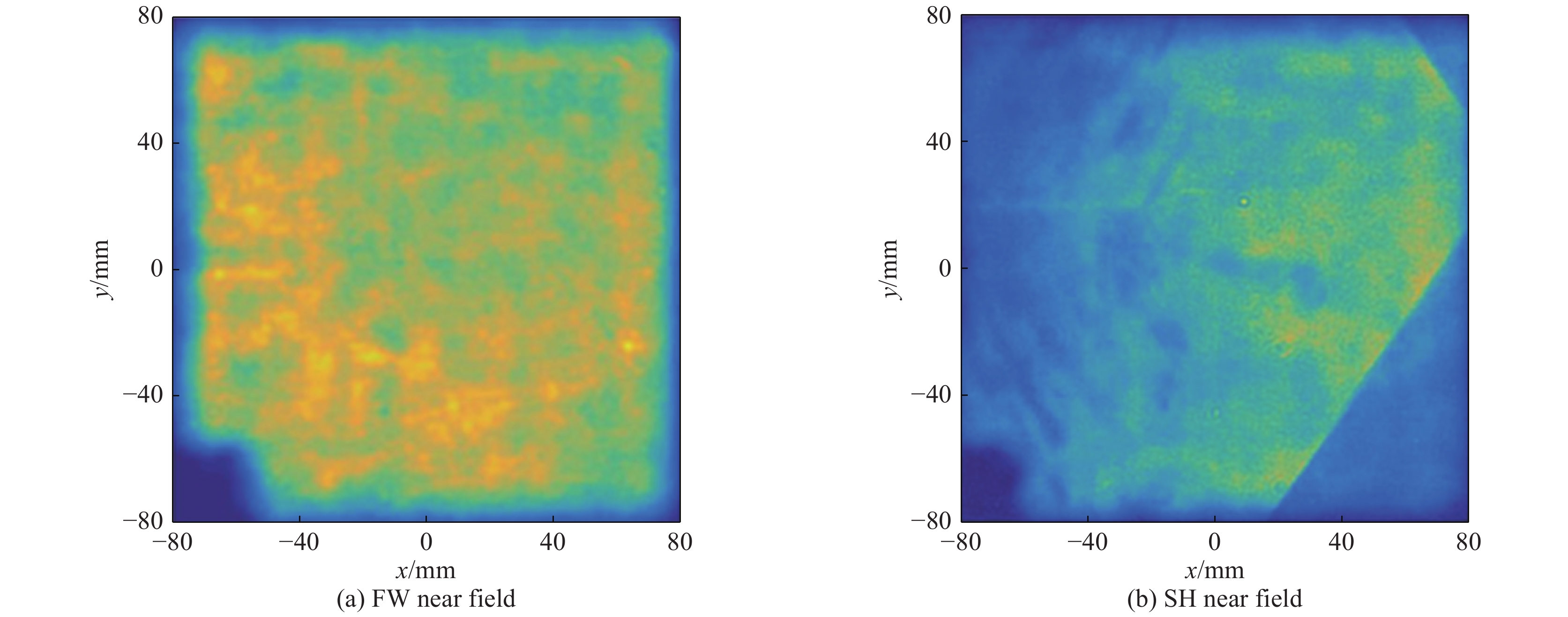
摘要: 低时间相干脉冲可有效提高激光与等离子相互作用中参量不稳定性的阈值,但高效频率转换难题是实现其工程应用瓶颈之一。系统分析了高功率激光驱动器已有的各类低时间相干脉冲频率转换技术的特性,并基于数值模拟和实验分析了部分掺氘DKDP晶体用于超辐射光倍频、三倍频的特性与工程应用可行性,结果表明掺氘17%左右DKDP晶体可以提高钕玻璃系统超辐射光的倍频效率,理论转换效率可达到约80%,10%梯度掺氘DKDP晶体则可实现5 THz带宽三倍频输出。Abstract: Low temporal coherence pulse can effectively increase the threshold of parametric instabilities in the laser and plasma interaction. However, frequency conversion efficiency is one of the bottlenecks in its engineering application. The characteristics of frequency conversion technologies of various low-coherence pulse for the high-power laser drivers are summarized in this paper, and based on numerical simulations and experiments, application feasibility of partial deuterium DKDP crystals for frequency doubling and tripling of super-luminescent light are analyzed in detail. The results show that 17% deuterium DKDP crystals can be used for efficient frequency doubling of super-luminescent light in neodymium glass systems, and the conversion efficiency can reach about 80%. 10% gradient deuterium DKDP crystals can be used for triple frequency of 5 THz bandwidth.
-
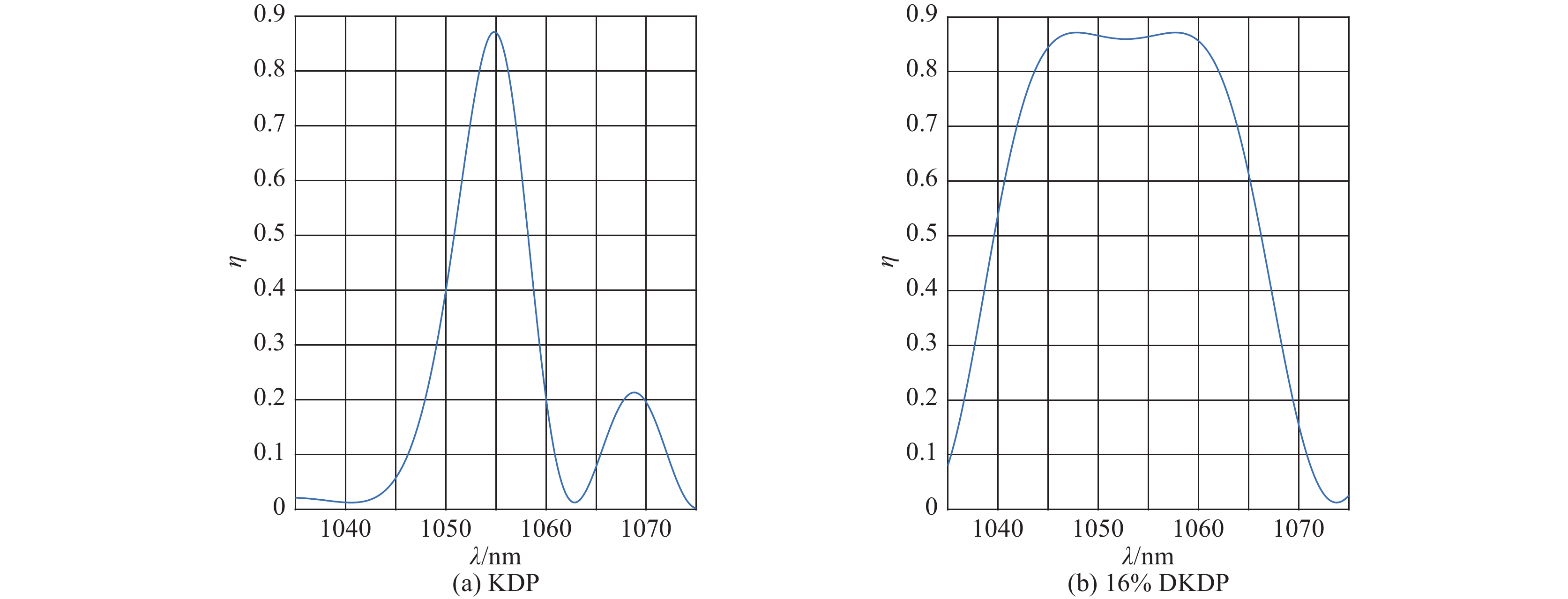
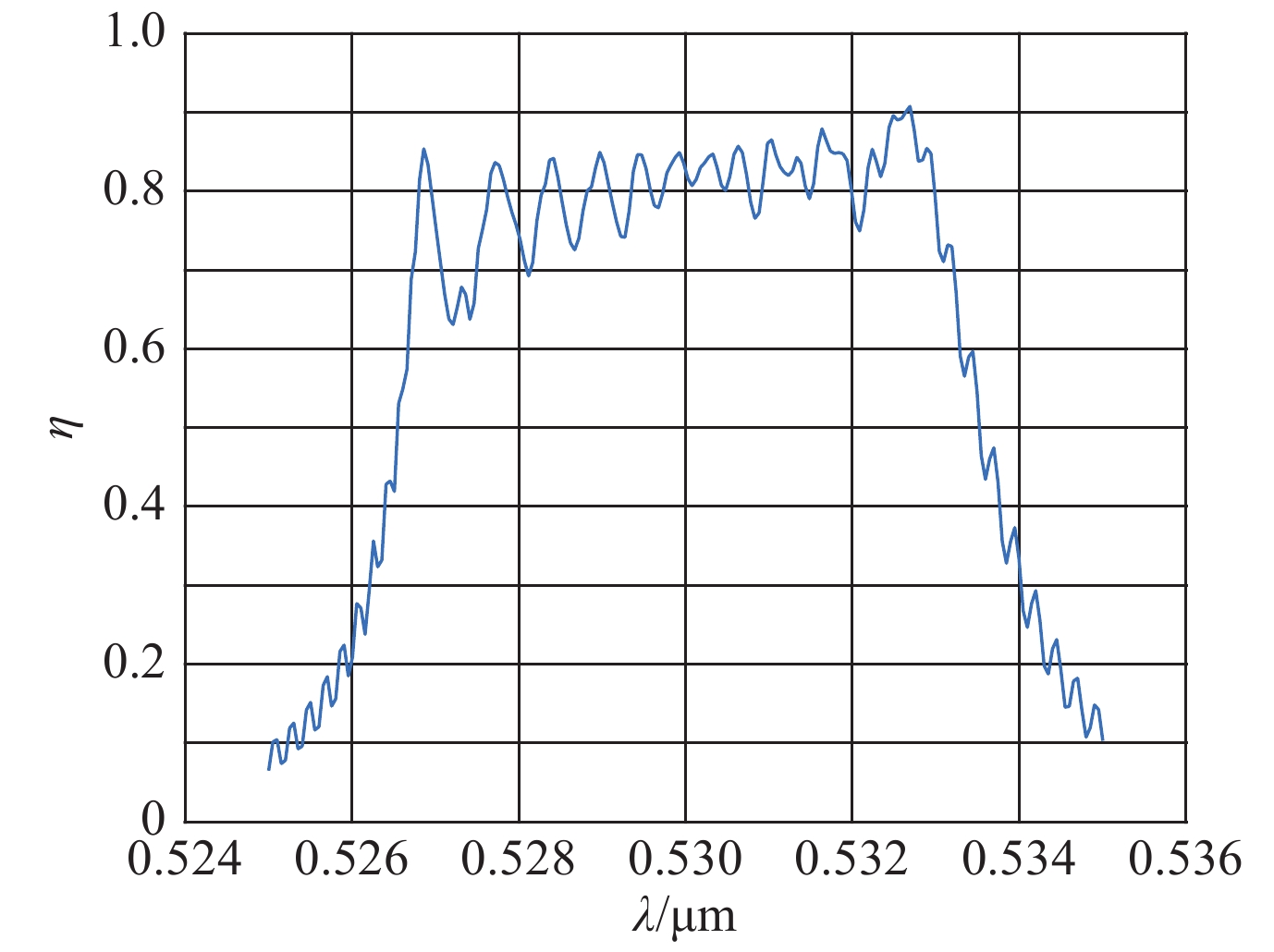
表 1 晶体的转换带宽比较(I~3 GW/cm2,l=20 mm)
Table 1. Comparison of conversion bandwidth with partial deuterium KDP
No. bandwidth @95% peak/nm bandwidth @90% peak/nm bandwidth @50% peak/nm KDP 2 3 7 16%DKDP 15 17 26 表 2 方程(3)中各物理量数值
Table 2. Value of parameters in equation(3)
αω/(cm−1) γ1/(cm2·GW−1) γ1/(cm2·GW−1) γ12/(cm2·GW−1) vF/(m·s−1) vH/(m·s−1) k1″/(fs2·mm−1) k1″/(fs2·mm−1) 0.058 2.3×10−7 3.5×10−7 0.08×10−7 c/1.5227 c/1.5223 −8.8 70.4 -
[1] Fedotov S I, Feoktistov L P, Osipov M V, et al. Lasers for ICF with a controllable function of mutual coherence of radiation[J]. Journal of Russian Laser Research, 2004, 25(1): 79-92. doi: 10.1023/B:JORR.0000012486.89881.d8 [2] Lindl J D, Amendt P, Berger R L, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility[J]. Physics of Plasmas, 2004, 11(2): 339-491. doi: 10.1063/1.1578638 [3] Smalyuk V A, Shvarts D, Betti R, et al. Role of hot-electron preheating in the compression of direct-drive imploding targets with cryogenic D2 ablators[J]. Physical Review Letters, 2008, 100(18): 1459-1469. [4] Karasik M, Weaver J L, Aglitskiy Y, et al. Suppression of laser nonuniformity imprinting using a thin high-z coating[J]. Physical Review Letters, 2015, 114: 085001. doi: 10.1103/PhysRevLett.114.085001 [5] Eimerl D, Campbell E M, Krupke W F, et al. StarDriver: a flexible laser driver for inertial confinement fusion and high energy density physics[J]. Journal of Fusion Energy, 2014, 33(5): 476-488. doi: 10.1007/s10894-014-9697-2 [6] Garanin S G, Derkach V N, Shnyagin R A. Formation of the uniform irradiation of a target in high-power laser facilities[J]. Quantum Electronics, 2004, 34(5): 427-446. doi: 10.1070/QE2004v034n05ABEH002700 [7] 邓锡铭, 梁向春, 陈泽尊, 等. 用透镜列阵实现大焦斑面的均匀照射[J]. 中国激光, 1985,12(5):3-6. (Deng Ximing, Liang Xiangchun, Chen Zezun, et al. Using lens array to achieve uniform illumination of large focal spot[J]. China Laser, 1985,12(5): 3-6 [8] Marozas J A. Fourier transform-based continuous phase-plate design technique: a high-pass phase-plate design as an application for OMEGA and the National Ignition Facility[J]. Journal of The Optical Society of America A-optics Image Science and Vision, 2007, 24(1): 74-83. doi: 10.1364/JOSAA.24.000074 [9] Marozas J A, Kelly J H. Angular spectrum representation of pulsed laser beams with two-dimensional smoothing by spectral dispersion[J]. LLE Rev, 1999, 78: 62-81. [10] Regan S, Marozas J A, Kelly J, et al. Experimental investigation of smoothing by spectral dispersion[J]. Journal of The Optical Society of America B-optical Physics, 2000, 17(9): 1483-1489. doi: 10.1364/JOSAB.17.001483 [11] Regan S, Marozas J A, Craxton R S, et al. Performance of 1-THz-bandwidth, two-dimensional smoothing by spectral dispersion and polarization smoothing of high-power, solid-state laser beams[J]. Journal of The Optical Society of America B-optical Physics, 2005, 22(5): 998-1002. doi: 10.1364/JOSAB.22.000998 [12] Moody J D, Michel P, Divol L, et al. Multistep redirection by cross-beam power transfer of ultrahigh-power lasers in a plasma[J]. Nature Physics, 2012, 8(4): 344-349. doi: 10.1038/nphys2239 [13] Betti R, Hurricane O A. Inertial-confinement fusion with lasers[J]. Nature Physics, 2016, 12(5): 435-448. doi: 10.1038/nphys3736 [14] Glenzer S H, Froula D H, Divol L, et al. Experiments and multiscale simulations of laser propagation through ignition-scale plasmas[J]. Nature Physics, 2007, 3(10): 716-719. doi: 10.1038/nphys709 [15] Labaune, Christine. Laser-driven fusion: Incoherent light on the road to ignition[J]. Nature Physics, 2007, 3(10): 680-682. doi: 10.1038/nphys742 [16] Santos J E, Silva L O, Bingham R, et al. White-light parametric instabilities in plasmas[J]. Physical Review Letters, 2007, 98: 235001. doi: 10.1103/PhysRevLett.98.235001 [17] Follett R K, Shaw J G, Myatt J F, et al. Thresholds of absolute instabilities driven by a broadband laser[J]. Physics of Plasmas, 2019, 26: 062111. doi: 10.1063/1.5098479 [18] Palastro J P, Shaw J G, Follett R K, et al. Resonance absorption of a broadband laser pulse[J]. Physics of Plasmas, 2018, 25: 123104. doi: 10.1063/1.5063589 [19] Eimerl D, Skupsky S, Campbell E M. StarDriver: Recent results on beam smoothing and LPI mitigation[J]. Journal of Physics Conference, 2016, 717: 012015. doi: 10.1088/1742-6596/717/1/012015 [20] Dorrer C. Statistical analysis of incoherent pulse shaping[J]. Optics Express, 2009, 17(5): 3341-3352. doi: 10.1364/OE.17.003341 [21] Spaeth M L, Manes K R, Bowers M, et al. National ignition facility laser system performance[J]. Fusion Science and Technology, 2016, 69(1): 366-394. doi: 10.13182/FST15-136 [22] Cui Y, Gao Y, Rao D, et al. High-energy low-temporal-coherence instantaneous broadband pulse system[J]. Optics Letters, 2019, 44(11): 2859-2862. doi: 10.1364/OL.44.002859 [23] Dorrer C, Hill E M, Zuegel J D, et al. High-energy parametric amplification of spectrally incoherent broadband pulses[J]. Optics Express, 2020, 28(1): 451-471. doi: 10.1364/OE.28.000451 [24] Franken P A, Hill A E, Peters C W, et al. Generation of optical harmonics[J]. Physical Review Letters, 1961, 7(4): 118-119. doi: 10.1103/PhysRevLett.7.118 [25] Bloembergen N, Pershan P S. Light waves at the boundary of nonlinear media[J]. Physical Review, 1962, 128(2): 606-622. doi: 10.1103/PhysRev.128.606 [26] Martinez O E. Achromatic phase matching for second harmonic generation of femtosecond pulses[J]. IEEE Journal Quantum Electronics, 1989, 25(12): 2464-2468. doi: 10.1109/3.40630 [27] Richman B A, Bisson S E, Trebino V, et al. Efficient broadband second-harmonic generation by dispersive achromatic nonlinear conversionusing only prisms[J]. Opt Lett, 1998, 23: 497. doi: 10.1364/OL.23.000497 [28] Ashihara S, Shimura T, Kuroda K. Group-velocity matched second-harmonic generation in tilted quasi-phase-matched gratings[J]. Journal of the Optical Society of America B, 2003, 20(5): 853-856. doi: 10.1364/JOSAB.20.000853 [29] Chen B Q, Zhang C, Hu C Y, et al. High-efficiency broadband high-harmonic generation from a single quasi-phase-matching nonlinear crystal[J]. Physical Review Letters, 2015, 115: 083902. doi: 10.1103/PhysRevLett.115.083902 [30] Zhang T R, Choo H R, Downer M C. Phase and group velocity matching for second harmonic generation of femtosecond pulses[J]. Applied Optics, 1990, 29(27): 3927-3933. doi: 10.1364/AO.29.003927 [31] Brown M. Increased spectral bandwidths in nonlinear conversion processes by use of multicrystal designs[J]. Optics Letters, 1998, 23(20): 1591-1593. doi: 10.1364/OL.23.001591 [32] Wang G Y, Garmire E M. High-efficiency generation of ultrashort second-harmonic pulses based on the erenkov geometry[J]. Optics Letters, 1994, 19(4): 254-256. doi: 10.1364/OL.19.000254 [33] Pronko M S, Lehmberg R H, Obenschain S P, et al. Efficient second harmonic conversion of broad-band high-peak-power Nd:glass laser radiation using large-aperture KDP crystals in quadrature[J]. IEEE Journal of Quantum Electronics, 1990, 26(2): 337-347. doi: 10.1109/3.44967 [34] Ji Lailin, Zhu Baoqiang, Liu Chong, et al. Optimization of quadrature frequency conversion with type-II KDP for second harmonic generation of the nanosecond chirp pulse at 1053 nm[J]. Chinese Optics Letters, 2014, 12(3): 70-74. [35] Eimerl D, Auerbach J M, Barker C E, et al. Multicrystal designs for efficient third-harmonic generation[J]. Optics Letters, 1997, 22(16): 1208-1210. doi: 10.1364/OL.22.001208 [36] Babushkin A, Craxton R S, Oskoui S, et al. Demonstration of the dual-tripler scheme for increased-bandwidth third-harmonic generation[J]. Optics Letters, 1998, 23(12): 927-929. doi: 10.1364/OL.23.000927 [37] Short R W, Skupsky S. Frequency conversion of broad-bandwidth laser light[J]. IEEE Journal of Quantum Electronics, 1990, 26(3): 580-588. doi: 10.1109/3.52136 [38] Skeldon M D, Craxton R S, Kessler T J, et al. Efficient harmonic generation with a broad-band laser[J]. IEEE Journal of Quantum Electronics, 1992, 28(5): 1389-1399. doi: 10.1109/3.135282 [39] Nakatsuka M, Miyanaga N, Kanabe T, et al. Partially coherent light sources for ICF experiment[C]// Proc of SPIE. 1993, 1870: 151-162. [40] Videau L, Boscheron A C L, Garnier J C, et al. Recent results of optical smoothing on the Phebus laser[C]// Proc of SPIE.1997, 3047: 757-762. [41] Boscheron A C, Sauteret C, Migus A, et al. Efficient broadband sum frequency based on controlled phase-modulated input fields: theory for 351-nm ultrabroadband or ultrashort-pulse generation[J]. Journal of The Optical Society of America B-optical Physics, 1996, 13(5): 818-826. doi: 10.1364/JOSAB.13.000818 [42] Raoult F, Boscheron A C, Husson D, et al. Ultrashort, intense ultraviolet pulse generation by efficient frequency tripling and adapted phase matching[J]. Optics Letters, 1999, 24(5): 354-356. doi: 10.1364/OL.24.000354 [43] 钱列加. 宽频带激光的啁啾匹配型三次谐波转换[J]. 光学学报, 1995, 15(6):662-664. (Qian Liejia. Chirp-matched third harmonic conversion of broadband lasers[J]. Acta Optics Sinica, 1995, 15(6): 662-664 doi: 10.3321/j.issn:0253-2239.1995.06.005 [44] 陈英, 王路露, 刘光灿, 等. 高功率钕玻璃激光的宽带谐波转换技术综述[J]. 激光与光电子学进展, 2014, 51(2):34-41. (Chen Ying, Wang Lulu, Liu Guangcan, et al. Survey on frequency conversion of broadband high power Nd:Glass laser[J]. Progress in Laser and Optoelectronics, 2014, 51(2): 34-41 [45] Rozenberg E, Arie A. Broadband and robust adiabatic second-harmonic generation by a temperature gradient in birefringently phase-matched lithium triborate crystal[J]. Optics Letters, 2019, 44(13): 3358-3361. doi: 10.1364/OL.44.003358 [46] Zhu H Y, Wang T, Zheng W G, et al. Efficient second harmonic generation of femtosecond laser at 1 μm[J]. Optics Express, 2004, 12(10): 2150-2155. doi: 10.1364/OPEX.12.002150 [47] Zheng Wanguo, Qian LieJia, Yuan Peng, et al. Second harmonic generation of femtosecond laser at one micron in a partially deuterated KDP[J]. Chinese Physics Letters, 2006, 23(1): 139-142. doi: 10.1088/0256-307X/23/1/041 [48] Dmitriev V G, Osipov M V, Puzyrev V N, et al. Nonlinear optical conversion of Nd:glass laser multimode radiation into the second harmonic in KDP crystal[J]. Journal of Physics B, 2012, 45: 165401. doi: 10.1088/0953-4075/45/16/165401 [49] Vasin B L, Korobkin Y V, Osipov M V, et al. Second-harmonic conversion of partially coherent radiation of neodymium glass laser[J]. Bulletin of the Lebedev Physics Institute, 2013, 40(7): 205-209. doi: 10.3103/S1068335613070063 [50] Ji L, Zhao X, Liu D, et al. High-efficiency second-harmonic generation of low-temporal-coherent light pulse[J]. Optics Letters, 2019, 44(17): 4359-4362. doi: 10.1364/OL.44.004359 -





 下载:
下载: