Recent progress in micro-mesoscopic study of dynamics of plastic deformation based on large-scale laser facilities
-
摘要: 微介观尺度下材料结构的实时演化行为是决定其动态力学性能的关键因素。大型激光装置作为集加载和诊断能力为一体的综合实验平台,为高温、高压、高应变率等极端条件下材料动态力学性能的微介观尺度研究提供了重要支撑。随着激光功率密度和脉冲整形能力的不断提升,实验所能探索的压力(101~103 GPa)及应变率(106~1010 s−1)范围不断突破;而利用激光打靶产生的高亮X射线脉冲作为探测源,建立动态衍射和成像技术,可以实现高空间和时间分辨率下材料塑性变形机制的实时原位研究。简要介绍了基于大型激光装置的原位微介观实验技术及其在材料塑性变形行为研究中的应用,系统梳理了近二十年来具有代表性的研究成果,阐明了相关研究对推动材料动态响应多尺度物理建模的重要价值。Abstract: The dynamic response of materials is strongly dependent on the temporal evolution of microstructures. As a comprehensive experimental platform integrating dynamic loading and in-situ diagnostic capability, large-scale laser facilities provide technical support to investigate micro-mesoscopic behaviors of materials under extreme conditions of high temperature, high pressure, and high strain rate. The use of high-power pulsed lasers to explore the response of materials under the pressure of tens of GPa up to several TPa, the time duration of nanoseconds, and the strain rate of 106−1010 s−1 is revealing novel mechanisms of plastic deformation and therefore strength evolution. This unique experimental tool, aided by advanced diagnostics, analysis, and characterization, including X-ray diffraction, absorption and imaging, allows us to make real-time observation on these new regimes with high spatial and temporal resolution. In this paper, we review the progress within the last 20 years in micro-mesoscopic dynamic probing techniques, based on large-scale laser facilities, and their applications in the study of dynamic plasticity and strength. At the end, we discuss the significance of these works to promote the multiscale modeling of the dynamic response of materials.
-
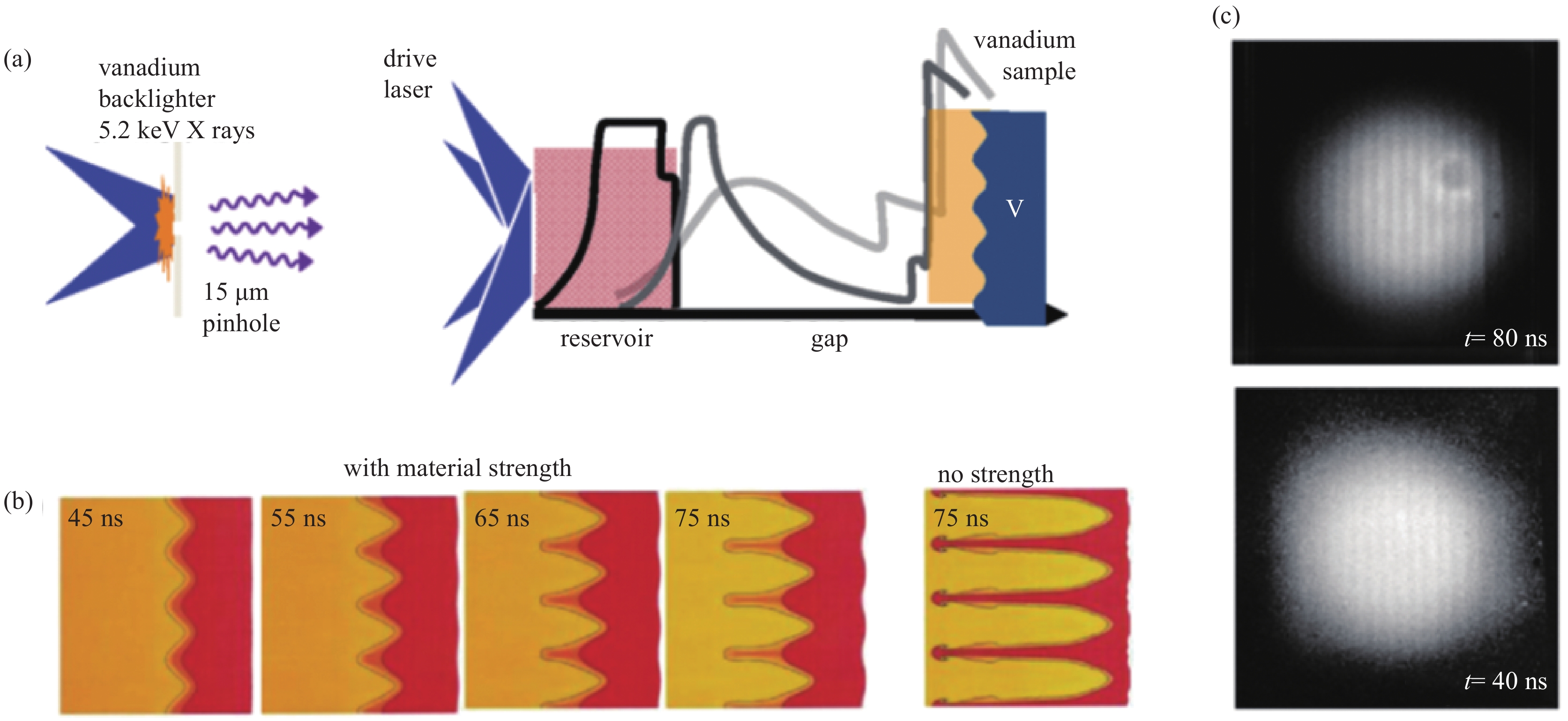
图 3 (a)实验构型示意图;(b)基于PTW模型二维辐射流体预测的45、55、65和75 ns时间内界面扰动增长密度图;(c)40和80 ns时刻X射线照相捕获的金属V中的界面扰动增长状态[31]
Figure 3. (a) Schematic illustrating the experimental configuration.(b) Density plots of the RT growth from 2D radiation-hydrodynamics simulations at 45,55,65,and 75 ns,using the PTW strength model.(c) Experimental X-ray radiographs of driven vanadium RT samples at 40 and 80 ns[31]
-
[1] Shewmon P G, Zackay V F. Response of metals to high velocity deformation[M]. NewYork: Interscience Publisher, 1961: 93-103 [2] Murr L, Meyers M, Niou C S, et al. Shock-induced deformation twinning in tantalum[J]. Acta materialia, 1997, 45(1): 157-175. doi: 10.1016/S1359-6454(96)00145-0 [3] Murr L E, Esquivel E. Observations of common microstructural issues associated with dynamic deformation phenomena: Twins, microbands, grain size effects, shear bands, and dynamic recrystallization[J]. Journal of Materials Science, 2004, 39(4): 1153-1168. doi: 10.1023/B:JMSC.0000013870.09241.c0 [4] Meyers M, Chen Y J, Marquis F, et al. High-strain, high-strain-rate behavior of tantalum[J]. Metallurgical and Materials Transactions A, 1995, 26(10): 2493-2501. doi: 10.1007/BF02669407 [5] Meyers M A, Gregori F, Kad B, et al. Laser-induced shock compression of monocrystalline copper: characterization and analysis[J]. Acta Materialia, 2003, 51(5): 1211-1228. doi: 10.1016/S1359-6454(02)00420-2 [6] Huang J, Gray III G. Substructure evolution and deformation modes in shock-loaded niobium[J]. Materials Science and Engineering: A, 1988, 103(2): 241-255. doi: 10.1016/0025-5416(88)90514-9 [7] Lu C H, Hahn E, Remington B, et al. Phase transformation in tantalum under extreme laser deformation[J]. Scientific Reports, 2015, 5: 15064. doi: 10.1038/srep15064 [8] Johnson Q, Mitchell A, Keeler RN, et al. X-ray diffraction during shock-wave compression[J]. Physical Review Letters, 1970, 25(16): 1099-1101. doi: 10.1103/PhysRevLett.25.1099 [9] Jensen B, Gupta Y. X-ray diffraction measurements in shock compressed magnesium doped LiF crystals[J]. Journal of Applied Physics, 2006, 100: 053512. doi: 10.1063/1.2244524 [10] Jensen B, Gupta Y. Time-resolved X-ray diffraction experiments to examine the elastic-plastic transition in shocked magnesium-doped LiF[J]. Journal of Applied Physics, 2008, 104: 013510. doi: 10.1063/1.2936899 [11] Turneaure S J, Gupta Y. Material strength determination in the shock compressed state using X-ray diffraction measurements[J]. Journal of Applied Physics, 2011, 109: 123510. doi: 10.1063/1.3597817 [12] Milathianaki D, Boutet S, Williams G, et al. Femtosecond visualization of lattice dynamics in shock-compressed matter[J]. Science, 2013, 342(6155): 220-223. doi: 10.1126/science.1239566 [13] Turneaure S J, Renganathan P, Winey J, et al. Twinning and dislocation evolution during shock compression and release of single crystals: real-time X-ray diffraction[J]. Physical Review Letters, 2018, 120: 265503. doi: 10.1103/PhysRevLett.120.265503 [14] Wehrenberg C, McGonegle D, Bolme C, et al. In situ X-ray diffraction measurement of shock-wave-driven twinning and lattice dynamics[J]. Nature, 2017, 550(7677): 496-499. doi: 10.1038/nature24061 [15] Sliwa M, McGonegle D, Wehrenberg C, et al. Femtosecond X-ray diffraction studies of the reversal of the microstructural effects of plastic deformation during shock release of tantalum[J]. Physical Review Letters, 2018, 120: 265502. doi: 10.1103/PhysRevLett.120.265502 [16] Sharma S M, Turneaure S J, Winey J, et al. Real-time observation of stacking faults in gold shock compressed to 150 GPa[J]. Physical Review X, 2020, 10: 011010. [17] Rudd R E, Germann T C, Remington B A, et al. Metal deformation and phase transitions at extremely high strain rates[J]. MRS Bulletin, 2011, 35(12): 999-1006. [18] Wang J, Coppari F, Smith R F, et al. X-ray diffraction of molybdenum under ramp compression to 1 TPa[J]. Physical Review B, 2016, 94: 104102. doi: 10.1103/PhysRevB.94.104102 [19] Wa rk, Justin. Time-resolved X-ray diffraction[J]. Contemporary Physics, 2006, 37(3): 205-218. [20] Ping Y, Coppari F. Laser shock XAFS studies at OMEGA facility[J]. High Pressure Research, 2016, 36(3): 303-314. doi: 10.1080/08957959.2016.1196203 [21] Glendinning S, Weber S, Bell P, et al. Laser-driven planar Rayleigh-Taylor instability experiments[J]. Physical Review Letters, 1992, 69(8): 1201-1204. doi: 10.1103/PhysRevLett.69.1201 [22] Rosenbluth M N. Handbook of Plasma Physics[M]. 1991, 3: 111 [23] Kalantar D H, Belak J, Bringa E, et al. High-pressure, high-strain-rate lattice response of shocked materials[J]. Physics of Plasmas, 2003, 10(5): 1569-1576. doi: 10.1063/1.1565118 [24] Kalantar D H, Belak J F, Collins G W, et al. Direct observation of the alpha-epsilon transition in shock-compressed iron via nanosecond X-ray diffraction[J]. Phys Rev Lett, 2005, 95: 075502. doi: 10.1103/PhysRevLett.95.075502 [25] Rygg J, Smith R, Lazicki A, et al. X-ray diffraction at the National Ignition Facility[J]. Review of Scientific Instruments, 2020, 91: 043902. doi: 10.1063/1.5129698 [26] Rygg J R, Eggert J H, Lazicki A E, et al. Powder diffraction from solids in the terapascal regime[J]. Rev Sci Instrum, 2012, 83: 113904. doi: 10.1063/1.4766464 [27] Yaakobi B, Boehly T R, Meyerhofer D D, et al. EXAFS measurement of iron bcc-to-hcp phase transformation in nanosecond-laser shocks[J]. Phys Rev Lett, 2005, 95: 075501. doi: 10.1103/PhysRevLett.95.075501 [28] Richtmyer R D. Taylor instability in shock acceleration of compressible fluids[J]. Communications on Pure and Applied Mathematics, 1960, 13(2): 297-319. doi: 10.1002/cpa.3160130207 [29] Taylor G. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I[J]. Proceedings of the Royal Society of London, 1950, 201(1065): 192-196. [30] Barnes J F, Blewett P J, McQueen R G, et al. Taylor instability in solids[J]. Journal of Applied Physics, 1974, 45(2): 727-732. doi: 10.1063/1.1663310 [31] Park H S, Lorenz K T, Cavallo R M, et al. Viscous Rayleigh-Taylor instability experiments at high pressure and strain rate[J]. Phys Rev Lett, 2010, 104: 135504. doi: 10.1103/PhysRevLett.104.135504 [32] Park H S, Remington B A, Becker R C, et al. Strong stabilization of the Rayleigh-Taylor instability by material strength at megabar pressures[J]. Physics of Plasmas, 2010, 17: 056314. doi: 10.1063/1.3363170 [33] Schneider M, Kad B, Meyers M, et al. Laser-induced shock compression of copper: Orientation and pressure decay effects[J]. Metallurgical and Materials Transactions A, 2004, 35(9): 2633-2646. doi: 10.1007/s11661-004-0209-2 [34] Schneider M S, Kad B, Kalantar D H, et al. Laser shock compression of copper and copper-aluminum alloys[J]. International Journal of Impact Engineering, 2005, 32(1/4): 473-507. [35] Foster J M, Comley A J, Case G S, et al. X-ray diffraction measurements of plasticity in shock-compressed vanadium in the region of 10–70 GPa[J]. Journal of Applied Physics, 2017, 122: 025117. doi: 10.1063/1.4994167 [36] Suggit M, Kimminau G, Hawreliak J, et al. Nanosecond X-ray Laue diffraction apparatus suitable for laser shock compression experiments[J]. Rev Sci Instrum, 2010, 81: 083902. doi: 10.1063/1.3455211 [37] Suggit M J, Higginbotham A, Hawreliak J A, et al. Nanosecond white-light Laue diffraction measurements of dislocation microstructure in shock-compressed single-crystal copper[J]. Nature Communications, 2012, 3(6): 1224-1229. [38] Stubley P G, Higginbotham A, Wark J S. Inelastic response of silicon to shock compression[J]. Computational Materials Science, 2016, 6: 121-126. [39] Wehrenberg C, Comley A, Barton N, et al. Lattice-level observation of the elastic-to-plastic relaxation process with subnanosecond resolution in shock-compressed Ta using time-resolved in situ Laue diffraction[J]. Physical Review B, 2015, 92: 104305. doi: 10.1103/PhysRevB.92.104305 [40] Murphy WJ, Higginbotham A, Kimminau G, et al. The strength of single crystal copper under uniaxial shock compression at 100 GPa[J]. Journal of Physics: Condensed Matter, 2010, 22: 065404. doi: 10.1088/0953-8984/22/6/065404 [41] Comley A J, Maddox B R, Rudd R E, et al. Strength of shock-loaded single-crystal tantalum [100] determined using in situ broadband X-ray Laue diffraction[J]. Phys Rev Lett, 2013, 110: 115501. doi: 10.1103/PhysRevLett.110.115501 [42] Hawreliak J A, El-Dasher B, Lorenzana H, et al. In situ X-ray diffraction measurements of the c/a ratio in the high-pressure ε phase of shock-compressed polycrystalline iron[J]. Physical Review B, 2011, 83: 144114. doi: 10.1103/PhysRevB.83.144114 [43] Remington B A, Park H S, Casey D T, et al. Rayleigh-Taylor instabilities in high-energy density settings on the National Ignition Facility[J]. Proceedings of the National Academy of Sciences, 2019, 116(37): 18233-18238. doi: 10.1073/pnas.1717236115 [44] Lorenz K T, Edwards M J, Glendinning S G, et al. Accessing ultrahigh-pressure, quasi-isentropic states of matter[J]. Physics of Plasmas, 2005, 12: 056309. doi: 10.1063/1.1873812 [45] Stebner A P, Wehrenberg C E, Li B, et al. Strength of tantalum shocked at ultrahigh pressures[J]. Materials Science and Engineering: A, 2018, 732: 220-227. doi: 10.1016/j.msea.2018.06.105 [46] Krygier A, Powell P, McNaney J, et al. Extreme hardening of Pb at high pressure and strain rate[J]. Physical Review Letters, 2019, 123: 205701. doi: 10.1103/PhysRevLett.123.205701 [47] Steinberg D, Cochran S, Guinan M. A constitutive model for metals applicable at high-strain rate[J]. Journal of Applied Physics, 1980, 51(3): 1498-1504. doi: 10.1063/1.327799 [48] Steinberg D, Lund C. A constitutive model for strain rates from 10−4 to 106 s−1[J]. Journal of Applied Physics, 1989, 65(4): 1528-1533. doi: 10.1063/1.342968 [49] Preston D L, Tonks D L, Wallace D C. Model of plastic deformation for extreme loading conditions[J]. Journal of Applied Physics, 2003, 93(1): 211-220. doi: 10.1063/1.1524706 [50] Barton N, Bernier J, Becker R, et al. A multiscale strength model for extreme loading conditions[J]. Journal of Applied Physics, 2011, 109: 073501. doi: 10.1063/1.3553718 [51] Becker R, Arsenlis A, Marian J, et al. Continuum level formulation and implementation of a multi-scale model for vanadium[R]. LLNLTR-416095, 2009. [52] Gleason A E. Soft metal gains Hulk-like strength[J]. Physics, 2019, 12: 125. doi: 10.1103/Physics.12.125 -




 下载:
下载: