激光产生温稠密物质的微观动力学过程及状态诊断

康冬冬; 曾启昱; 张珅; 王小伟; 戴佳钰

doi:10.11884/HPLPB202032.200121

激光产生温稠密物质的微观动力学过程及状态诊断

doi: 10.11884/HPLPB202032.200121

国防科技大学文理学院物理系，长沙 410072

基金项目: 国家重点研发计划项目（2017YFA0403200）；科学挑战专题项目（TZ2016001）；国家自然科学基金项目（11874424，11774429，11904401，U1830206）

详细信息

作者简介:
康冬冬（1984—），男，博士，副教授，从事高能量密度物理研究；ddkang@nudt.edu.cn

通讯作者:
戴佳钰（1981—），男，博士，教授，从事原子与分子物理和高能量密度物理研究；jydai@nudt.edu.cn

中图分类号: O522⁺.2
计量
- 文章访问数: 2212
- HTML全文浏览量: 574
- PDF下载量: 165
- 被引次数: 0
出版历程
- 收稿日期: 2020-05-13
- 修回日期: 2020-07-15
- 刊出日期: 2020-08-15

Dynamics and micro-structures in generation of warm dense matter using intense laser

Department of Physics, College of Liberal Arts and Sciences, National University of Defense Technology, Changsha 410072, China

摘要

摘要: 随着大型激光装置的建立和精密测量技术的发展，强激光与固体相互作用成为实验室产生温稠密物质的一个重要手段。温稠密物质的结构复杂性、瞬态性和非平衡性给理论建模和实验测量带来了巨大挑战。本文系统介绍了激光产生温稠密物质的实验手段和理论模拟方法方面的重要进展，分析了其中的电子激发动力学、电子-离子能量弛豫过程、离子动力学等物理过程，总结了温稠密物质状态诊断的实验技术和理论方法，并论述了激光产生温稠密物质的发展趋势。
- 温稠密物质 /
- 激光与物质相互作用 /
- 电子动力学 /
- 电子-离子能量弛豫 /
- 离子动力学 /
- 状态诊断
Abstract: With the establishment of high-power laser facilities and the development of precise measurement technology, the interaction between high-power lasers and solids has become an important path to generate warm dense matter in laboratories. The structural complexity, transients and non-equilibrium of warm dense matter have brought great challenges to theoretical modeling and experimental measurements. This paper systematically reviews the important advances in the experimental methods and theoretical simulation methods in laser-generating warm dense matter, analyzes the physical processes such as electron excitation dynamics, electron-ion energy relaxation, and ionic dynamics. It summarizes the experimental techniques and theoretical methods of state diagnosis of warm dense matter, and discusses the development trend of laser-generating warm dense matter.
- warm dense matter /
- laser-matter interaction /
- electronic dynamics /
- electron-ion relaxation /
- ionic dynamics /
- state diagnosis

HTML全文

图 1 超快激光产生温稠密金的演化图^[84]

Figure 1. Contour plots of parameters of the laser-generated warm dense gold^[84]

下载: 全尺寸图片幻灯片

图 2 完全熔化时间与激光能量密度的关系^[84]

Figure 2. Melting time as a function of energy density of laser^[84]

下载: 全尺寸图片幻灯片

图 3 电子-离子温度随时间变化图^[14]

Figure 3. Time evolution curves of electron and ion temperature^[14]

下载: 全尺寸图片幻灯片

图 4 不同密度条件下电子温度和离子温度随时间的演化及不同理论方法和分子动力学模拟方法计算库伦对数比较^[15]

Figure 4. Temporal evolution of ion and electron temperatures at different densities and Coulomb logarithms calculated from various theoretical methods and molecular dynamics simulations^[15]

下载: 全尺寸图片幻灯片

图 5 四种温度密度状态氢的电导率和光吸收系数^[66]以及不同温度下的氢的电导率随压强的变化关系^[107]

Figure 5. Electrical conductivity and optical absorption coefficient for four state points of hydrogen^[66]and electrical conductivity of hydrogen^[107]

下载: 全尺寸图片幻灯片

图 6 高温下氢的电导率随温度的变化关系^[108]

Figure 6. Electrical conductivity curves of hydrogen as a function of temperature^[108]

下载: 全尺寸图片幻灯片

参考文献(111)

[1]	Drake R P. High-energy-density physics: Fundamentals, inertial fusion and experimental astrophysics[M]. Berlin: Springer, 2006.
[2]	Graziani F, Desjarlais M P, Redmer R, et al. Frontiers and challenges in warm dense matter[M]. Berlin: Springer, 2014.
[3]	Moses E I, Boyd R N, Remington B A, et al. The National Ignition Facility: Ushering in a new age for high energy density science[J]. Phys Plasmas, 2009, 16: 041006. doi: 10.1063/1.3116505
[4]	Kang Dongdong, Dai Jiayu. Dynamic electron-ion collisions and nuclear quantum effects in quantum simulation of warm dense matter[J]. J Phys: Condens Matter, 2018, 30: 073002. doi: 10.1088/1361-648X/aa9e29
[5]	郑君, 陈其峰, 顾云军, 等. 强粒子束产生温稠密物质热力学状态估计[J]. 强激光与粒子束, 2014, 26:035102. (Zheng Jun, Chen Qifeng, Gu Yunjun, et al. Thermodynamic properties of warm dense matter generated by strong particle beams[J]. High Power Laser and Particle Beams, 2014, 26: 035102 doi: 10.3788/HPLPB20142603.35102
[6]	陈其峰, 顾云军, 郑君, 等. 温密物质特性研究进展与评述[J]. 科学通报, 2017, 62(8):812-823. (Chen Qifeng, Gu Yunjun, Zheng Jun, et al. Review and progress in the study of properties of warm dense matter[J]. Chin Sci Bull, 2017, 62(8): 812-823 doi: 10.1360/N972016-00471
[7]	Boehly T R, Hicks D G, Celliers P M, et al. Properties of fluid deuterium under double-shock compression to several Mbar[J]. Phys Plasmas, 2004, 11: L49-L52. doi: 10.1063/1.1778164
[8]	Nora R, Theobald W, Betti R, et al. Gigabar spherical shock generation on the OMEGA laser[J]. Phys Rev Lett, 2015, 114: 045001. doi: 10.1103/PhysRevLett.114.045001
[9]	Kritcher A L, Döppner T, Swift D, et al. Probing matter at Gbar pressures at the NIF[J]. High Energy Density Phys, 2014, 10: 27-34. doi: 10.1016/j.hedp.2013.11.002
[10]	Zhao Yang, Yang Jiamin, Zhang Jiyan, et al. K-shell photoabsorption edge of strongly coupled matter driven by laser-converted radiation[J]. Phys Rev Lett, 2013, 111: 155003. doi: 10.1103/PhysRevLett.111.155003
[11]	Qing Bo, Zhao Yang, Wei Minxi, et al. Time-resolved transmission measurements of warm dense iron plasma[J]. Chin Phys Lett, 2016, 33: 035203. doi: 10.1088/0256-307X/33/3/035203
[12]	Zhao Yang, Zhang Zhiyu, Qing Bo, et al. K-shell photoabsorption edge of strongly coupled aluminum driven by laser-converted radiation[J]. Europhys Lett, 2017, 117: 65001. doi: 10.1209/0295-5075/117/65001
[13]	Anisimov S I, Kapeliovich B L, Perelman T L. Electron emission from metal surfaces exposed to ultrashort laser pulses[J]. EkspTeorFiz, 1974, 66: 375-377.
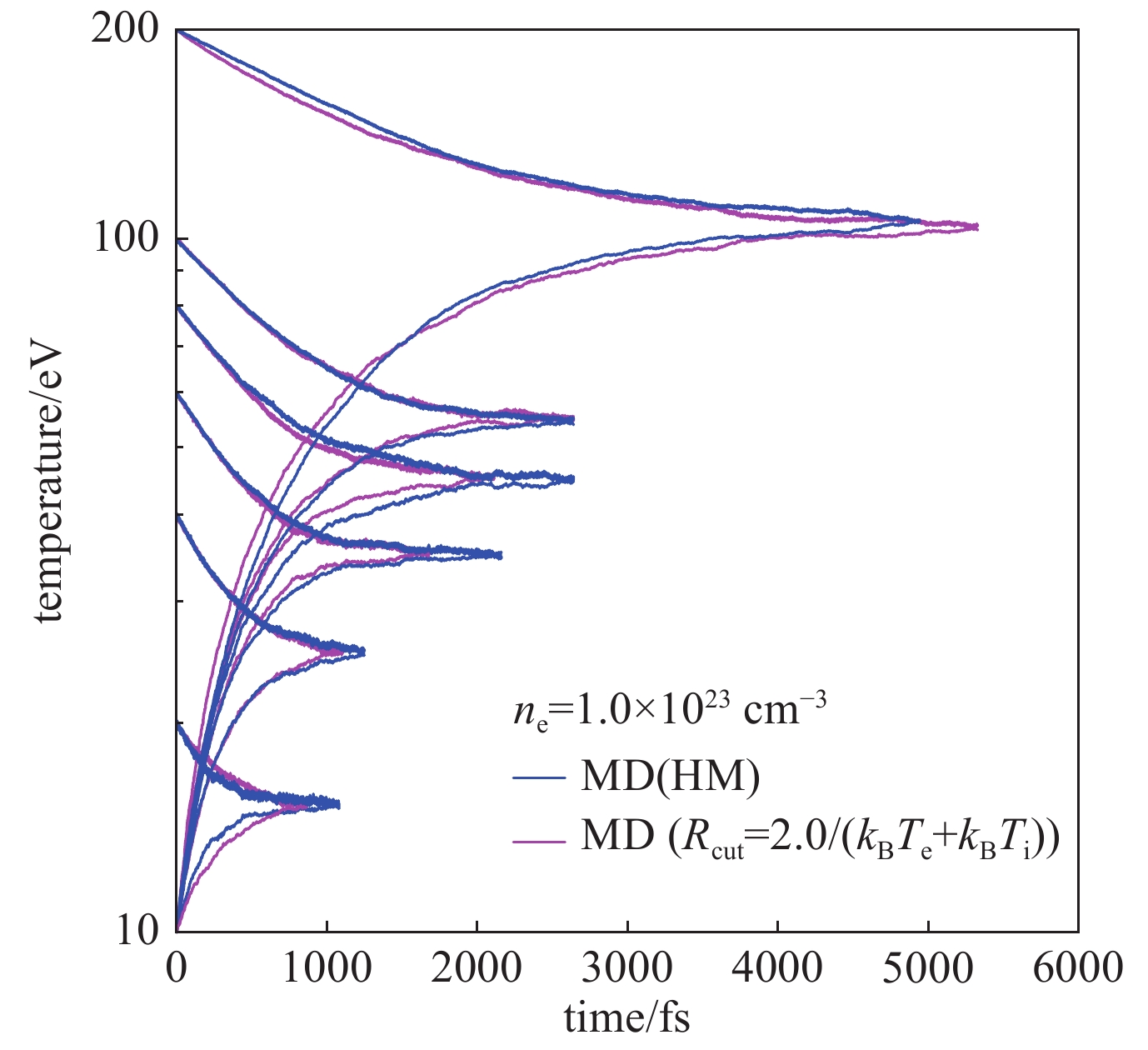
[14]	Ma Qian, Dai Jiayu, Kang Dongdong, et al. Molecular dynamics simulation of electron-ion temperature relaxation in dense hydrogen: A scheme of truncated Coulomb potential[J]. High Energy Density Phys, 2014, 13: 34-39. doi: 10.1016/j.hedp.2014.09.004
[15]	Ma Qian, Dai Jiayu, Kang Dongdong, et al. Extremely low electron-ion temperature relaxation rates in warm dense hydrogen: Interplay between quantum electrons and coupled ions[J]. Phys Rev Lett, 2019, 122: 015001. doi: 10.1103/PhysRevLett.122.015001
[16]	Ceperley D M. Path integrals in the theory of condensed helium[J]. Rev Mod Phys, 1995, 67(2): 279-355. doi: 10.1103/RevModPhys.67.279
[17]	Schoof T, Groth S, Vorberger J, et al. Ab initio thermodynamic results for the degenerate electron gas at finite temperature[J]. Phys Rev Lett, 2015, 115: 130402. doi: 10.1103/PhysRevLett.115.130402
[18]	Driver K P, Militzer B. All-electron path integral Monte Carlo simulations of warm dense matter: Application to water and carbon plasmas[J]. Phys Rev Lett, 2012, 108: 115502. doi: 10.1103/PhysRevLett.108.115502
[19]	Collins L, Kwon I, Kress J, et al. Quantum molecular dynamics simulations of hot, dense hydrogen[J]. Phys Rev E, 1995, 52(6): 6202-6218. doi: 10.1103/PhysRevE.52.6202
[20]	Holst B, Redmer R, Desjarlais M P. Thermophysical properties of warm dense hydrogen using quantum molecular dynamics simulations[J]. Phys Rev B, 2008, 77: 184201. doi: 10.1103/PhysRevB.77.184201
[21]	Lambert F, Clérouin J, Zérah G. Very-high-temperature molecular dynamics[J]. Phys Rev E, 2006, 73: 016403. doi: 10.1103/PhysRevE.73.016403
[22]	Dai Jiayu, Yuan Jianmin. Large-scale efficient Langevin dynamics, and why it works[J]. Europhys Lett, 2009, 88: 20001. doi: 10.1209/0295-5075/88/20001
[23]	Dai Jiayu, Hou Yong, Yuan Jianmin. Unified first principles description from warm dense matter to ideal ionized gas plasma: Electron-ion collisions induced friction[J]. Phys Rev Lett, 2010, 104: 245001. doi: 10.1103/PhysRevLett.104.245001
[24]	Dai Jiayu, Hou Yong, Yuan Jianmin. Quantum Langevin molecular dynamic determination of the solar-interior equation of state[J]. Astrophys J, 2010, 721: 1158. doi: 10.1088/0004-637X/721/2/1158
[25]	Dai Jiayu, Kang Dongdong, Zhao Zengxiu, et al. Dynamic ionic clusters with flowing electron bubbles from warm to hot dense iron along the Hugoniot curve[J]. Phys Rev Lett, 2012, 109: 175701. doi: 10.1103/PhysRevLett.109.175701
[26]	Hou Yong, JinFengtao, Yuan Jianmin. Influence of the electronic energy level broadening on the ionization of atoms in hot and dense plasmas: An average atom model demonstration[J]. Phys Plasmas, 2006, 13: 093301. doi: 10.1063/1.2338023
[27]	Hou Yong, Yuan Jianmin. Alternative ion-ion pair-potential model applied to molecular dynamics simulations of hot and dense plasmas: Al and Fe as examples[J]. Phys Rev E, 2009, 79: 016402. doi: 10.1103/PhysRevE.79.016402
[28]	Su J T, Goddard III W A. Excited electron dynamics modeling of warm dense matter[J]. Phys Rev Lett, 2007, 99: 185003. doi: 10.1103/PhysRevLett.99.185003
[29]	Su J T, Goddard III W A. The dynamics of highly excited electronic systems: Applications of the electron force field[J]. J Chem Phys, 2009, 131: 244501. doi: 10.1063/1.3272671
[30]	Gu Yunjun, Chen Qifeng, Zheng Jian, et al. Multishock comparison of dense gaseous H<sub>2</sub>+He mixtures up to 30 GPa[J]. J Chem Phys, 2009, 130: 184506. doi: 10.1063/1.3124562
[31]	Zheng Jian, Chen Qifeng, Gu Yunjun, et al. Hugoniot measurements of double-shocked precompressed dense xenon plasmas[J]. Phys Rev E, 2012, 86: 066406. doi: 10.1103/PhysRevE.86.066406
[32]	Gu Yunjun, Chen Qifeng, Zheng Jian, et al. The equation of state, shock-induced molecule dissociation, and transparency loss for multi-compressed dense gaseous H<sub>2</sub>+D<sub>2</sub> mixtures[J]. J Appl Phys, 2012, 111: 013513. doi: 10.1063/1.3675281
[33]	Zheng Jian, Chen Qifeng, Gu Yunjun, et al. Thermodynamics, compressibility, and phase diagram: Shock compression of supercritical fluid xenon[J]. J Chem Phys, 2014, 141: 124201. doi: 10.1063/1.4896071
[34]	Zheng Jian, Chen Qifeng, Gu Yunjun, et al. Multishock compression properties of warm dense argon[J]. Sci Rep, 2015, 5: 16041. doi: 10.1038/srep16041
[35]	Wang Cong, He Xiantu, Zhang Ping. Ab initio simulations of dense helium plasmas[J]. Phys Rev Lett, 2011, 106: 145002. doi: 10.1103/PhysRevLett.106.145002
[36]	Wang Cong, He Xiantu, Zhang Ping. Thermophysical properties of hydrogen-helium mixtures: Re-examination of the mixing rules via quantum molecular dynamics simulations[J]. Phys Rev E, 2013, 88: 033106. doi: 10.1103/PhysRevE.88.033106
[37]	Zhang Shen, Wang Hongwei, Kang Wei, et al. Extended application of Kohn-Sham first-principles molecular dynamics method with plane wave approximation at high energy—From cold materials to hot dense plasmas[J]. Phys Plasmas, 2016, 23: 042707. doi: 10.1063/1.4947212
[38]	吉诚, 李冰, 杨文革, 等. 静态超高压下氢的晶体结构实验研究[J]. 高压物理学报, 2020, 34:020101. (Ji Cheng, Li Bing, Yang Wenge, et al. Crystallographic studies of ultra-dense solid hydrogen[J]. Chin J High Press Phys, 2020, 34: 020101 doi: 10.11858/gywlxb.20200520
[39]	Celliers M, Loubeyre P, Eggert J H, et al. Insulator-to-conduction transition in dense fluid helium[J]. Phys Rev Lett, 2010, 104: 184503. doi: 10.1103/PhysRevLett.104.184503
[40]	Loubeyre P, Brygoo S, Eggert J H, et al. Extended data set for the equation of state of warm dense hydrogen isotopes[J]. Phys Rev B, 2012, 86: 144115. doi: 10.1103/PhysRevB.86.144115
[41]	李牧, 孙承纬, 赵剑衡. 固体材料高功率激光斜波压缩研究进展[J]. 爆炸与冲击, 2015, 35(2):145-156. (Li Mu, Sun Chengwei, Zhao Jianheng. Progress in high-power laser ramp compression of solids[J]. Explosion and Shock Waves, 2015, 35(2): 145-156 doi: 10.11883/1001-1455(2015)02-0145-12
[42]	种涛, 赵剑衡, 谭福利, 等. 斜波压缩下锡的相变动力学特性[J]. 高压物理学报, 2020, 34:011101. (Chong Tao, Zhao Jianheng, Tan Fuli, et al. Dynamic characteristics of phase transition of tin under ramp wave loading[J]. Chin J High Press Phys, 2020, 34: 011101 doi: 10.11858/gywlxb.20190828
[43]	蒲昱东, 陈伯伦, 黄天晅, 等. 激光间接驱动惯性约束聚变内爆物理实验研究[J]. 强激光与粒子束, 2015, 27:032015. (Pu Yudong, Chen Bolun, Huang Tianxuan, et al. Experimental studies of implosion physics of indirect-drive inertial confinement fusion[J]. High Power Laser and Particle Beams, 2015, 27: 032015 doi: 10.11884/HPLPB201527.032015
[44]	Campbell E M, Goncharov V N, Sangster T C, et al. Laser-direct-drive program: Promise, challenge, and path forward[J]. Matter Radiat Extremes, 2017, 2: 37-54. doi: 10.1016/j.mre.2017.03.001
[45]	Ping Y, Correa A A, Ogitsu T, et al. Warm dense matter created by isochoric laser heating[J]. High Energy Density Phys, 2010, 6(2): 246-257. doi: 10.1016/j.hedp.2009.12.009
[46]	Amano Y, Miki Y, Takahashi T, et al. Isochoric heating of foamed metal using pulsed power discharge as a making technique of warm dense matter[J]. Rev Sci Instrum, 2012, 83: 085107. doi: 10.1063/1.4742986
[47]	Glenzer S H, Gregori G, Lee R W, et al. Demonstration of spectrally resolved X-ray scattering in dense plasmas[J]. Phys Rev Lett, 2003, 90: 175002. doi: 10.1103/PhysRevLett.90.175002
[48]	Passoni M, Bertagna L, Zani A. Target normal sheath acceleration: theory, comparison with experiments and future perspectives[J]. New J Phys, 2010, 12: 045012. doi: 10.1088/1367-2630/12/4/045012
[49]	Liseykina T V, Borghesi M, Macchi A, et al. Radiation pressure acceleration by ultraintense laser pulses[J]. Plasma Phys Control Fusion, 2008, 50: 124033. doi: 10.1088/0741-3335/50/12/124033
[50]	Yan X Q, Lin C, Sheng Z M, et al. Generating high-current monoenergetic proton beams by a circularly polarized laser pulse in the phase-stable acceleration regime[J]. Phys Rev Lett, 2008, 100: 135003. doi: 10.1103/PhysRevLett.100.135003
[51]	Hoarty D J, Guymer T, James S F, et al. Equation of state studies of warm dense matter samples heated by laser produced proton beams[J]. High Energy Density Phys, 2012, 8(1): 50-54. doi: 10.1016/j.hedp.2011.11.008
[52]	Sperling P, Gamboa E J, Lee H J, et al. Free-electron X-ray laser measurements of collisional-damped plasmons in isochorically heated warm dense matter[J]. Phys Rev Lett, 2015, 115: 115001. doi: 10.1103/PhysRevLett.115.115001
[53]	Vinko S M, Ciricosta O, Cho B I, et al. Creation and diagnosis of a solid-density plasma with an X-ray free-electron laser[J]. Nature, 2012, 482: 59-62. doi: 10.1038/nature10746
[54]	Bieniosek F M, Barnard J J, Friedman A. Ion-beam-driven warm dense matter experiments[J]. J Phys: Conf Ser, 2010, 44: 032028.
[55]	Schonlein A, Boutoux G, Pikuz S, et al. Generation and characterization of warm dense matter isochorically heated by laser-induced relativistic electrons in a wire target[J]. Europhys Lett, 2016, 114: 45002. doi: 10.1209/0295-5075/114/45002
[56]	Vorberger J, Donko Z, Tkachenko I M, et al. Dynamic ion structure factor of warm dense matter[J]. Phys Rev Lett, 2012, 109: 225001. doi: 10.1103/PhysRevLett.109.225001
[57]	Mahieu B, Jourdain N, Ta Phuoc K, et al. Probing warm dense matter using femtosecond X-ray absorption spectroscopy with a laser-produced betatron source[J]. Nat Commun, 2018, 9: 3276. doi: 10.1038/s41467-018-05791-4
[58]	Hohenberg P, Kohn W. Inhomogeneous electron gas[J]. Phys Rev, 1964, 136: B864. doi: 10.1103/PhysRev.136.B864
[59]	Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects[J]. Phys Rev, 1965, 140: A1133. doi: 10.1103/PhysRev.140.A1133
[60]	Mermin N D. Thermal properties of the inhomogeneous electron gas[J]. Phys Rev, 1965, 137: A1441. doi: 10.1103/PhysRev.137.A1441
[61]	Witt W C, del Rio B G, Dieterich J M. Orbital-free density functional theory for materials research[J]. J Mater Res, 2018, 33(7): 777-795. doi: 10.1557/jmr.2017.462
[62]	Dai Jiayu, Hou Yong, Yuan Jianmin. Influence of ordered structures on electrical conductivity and XANES from warm and hot dense matter[J]. High Energy Density Phys, 2011, 7: 84. doi: 10.1016/j.hedp.2011.02.002
[63]	Dai Jiayu, Hou Yong, Kang Dongdong, et al. Structure, equation of state, diffusion and viscosity of warm dense Fe under the conditions of a giant planet core[J]. New J Phys, 2013, 15: 045003. doi: 10.1088/1367-2630/15/4/045003
[64]	Dai Jiayu, Gao Cheng, Sun Huayang, et al. Electronic and optical properties of warm dense lithium: strong coupling effects[J]. J Phys B, 2017, 50: 184004. doi: 10.1088/1361-6455/aa84f8
[65]	Kang Dongdong, Dai Jiayu, Sun Huayang, et al. Quantum simulation of thermally-driven phase transition and oxygen K-edge X-ray absorption of high-pressure ice[J]. Sci Rep, 2013, 3: 3272. doi: 10.1038/srep03272
[66]	Kang Dongdong, Sun Huayang, Dai Jiayu, et al. Nuclear quantum dynamics in dense hydrogen[J]. Sci Rep, 2014, 4: 5484.
[67]	Su J T, Goddard III W A. Mechanisms of Auger-induced chemistry derived from wave packet dynamics[J]. Proc Natl Acad Sci USA, 2009, 106(4): 1001-1005. doi: 10.1073/pnas.0812087106
[68]	Kim H, Su J T, Goddard III W A. High-temperature high-pressure phases of lithium from electron force field (eFF) quantum electron dynamics simulations[J]. Proc Natl Acad Sci USA, 2011, 108(37): 15101-15105. doi: 10.1073/pnas.1110322108
[69]	Kaganov M l, Lifshitz I M, Tanatarov L V. Relaxation between electrons and the crystalline lattice[J]. J Exp Theor Phys, 1957, 4(2): 173.
[70]	Ivanov D S, Zhigilei L V. Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films[J]. Phys Rev B, 2003, 68: 064114. doi: 10.1103/PhysRevB.68.064114
[71]	Duffy D M, Rutherford A M. Including the effects of electronic stopping and electron–ion interactions in radiation damage simulations[J]. J Phys: Condens Matter, 2006, 19: 016207.
[72]	Rutherford A M, Duffy D M. The effect of electron–ion interactions on radiation damage simulations[J]. J Phys: Condens Matter, 2007, 19(49): 496201. doi: 10.1088/0953-8984/19/49/496201
[73]	Norman G E, Starikov S V, Stegailov V V, et al. Atomistic modeling of warm dense matter in the two-temperature state[J]. Contrib Plasma Phys, 2013, 53(2): 129-139. doi: 10.1002/ctpp.201310025
[74]	Recoules V, Clérouin J, Zérah G, et al. Effect of intense laser irradiation on the lattice stability of semiconductors and metals[J]. Phys Rev Lett, 2006, 96: 055503. doi: 10.1103/PhysRevLett.96.055503
[75]	Lin Zhibin, Zhigilei L V. Time-resolved diffraction profiles and atomic dynamics in short-pulse laser-induced structural transformations: Molecular dynamics study[J]. Phys Rev B, 2006, 73: 184113. doi: 10.1103/PhysRevB.73.184113
[76]	Ivanov D S, Zhigilei L V. Effect of pressure relaxation on the mechanisms of short-pulse laser melting[J]. Phys Rev Lett, 2003, 91: 105701. doi: 10.1103/PhysRevLett.91.105701
[77]	Zhigilei L V, Garrison B J. Pressure waves in microscopic simulations of laser ablation[J]. Mat Res Soc Symp Proc, 1999, 538: 491.
[78]	Etcheverry J I, Mesaros M. Molecular dynamics simulation of the production of acoustic waves by pulsed laser irradiation[J]. Phys Rev B, 1999, 60(13): 9430-9434. doi: 10.1103/PhysRevB.60.9430
[79]	Ernstorfer R, Harb M, Hebeisen C T, et al. The Formation of warm dense matter: Experimental evidence for electronic bond hardening in gold[J]. Science, 2009, 323: 1033-1037. doi: 10.1126/science.1162697
[80]	Daraszewicz S L, Giret Y, Naruse N, et al. Structural dynamics of laser-irradiated gold nanofilms[J]. Phys Rev B, 2013, 88: 184101. doi: 10.1103/PhysRevB.88.184101
[81]	Giret Y, Naruse N, Daraszewicz S L, et al. Determination of transient atomic structure of laser-excited materials from time-resolved diffraction data[J]. Appl Phys Lett, 2013, 103: 253107. doi: 10.1063/1.4847695
[82]	Mo M Z, Chen Z, Li R K, et al. Heterogeneous to homogeneous melting transition visualized with ultrafast electron diffraction[J]. Science, 2018, 360(6396): 1451-1455. doi: 10.1126/science.aar2058
[83]	Chen Z, Mo M, Soulard L, et al. Interatomic potential in the nonequilibrium warm dense matter regime[J]. Phys Rev Lett, 2018, 121: 075002. doi: 10.1103/PhysRevLett.121.075002
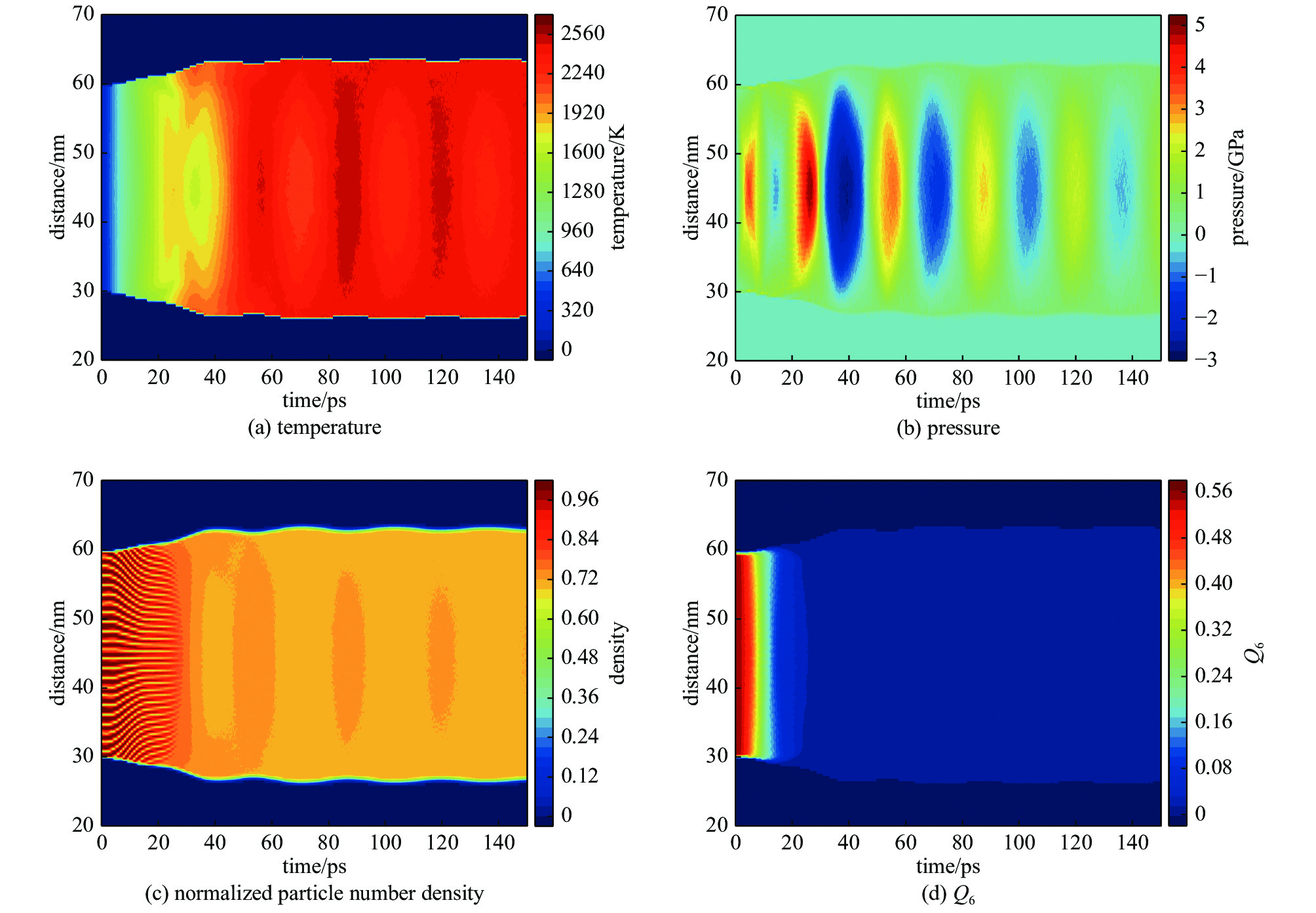
[84]	Zeng Qiyu, Dai Jiayu. Structural transition dynamics of the formation of warm dense gold: From an atomic scale view[J]. Science China: Physics, Mechanics & Astronomy, 2020, 63: 263011. doi: 10.1007/s11433-019-1466-2
[85]	Silvestrelli P L, Alavi A, Parrinello M, et al. Structural, dynamical, electronic, and bonding properties of laser-heated silicon: An ab initio molecular-dynamics study[J]. Phys Rev B, 1997, 56(7): 3806. doi: 10.1103/PhysRevB.56.3806
[86]	Gambirasio A, Bernasconi M, Colombo L. Laser-induced melting of silicon: A tight-binding molecular dynamics simulation[J]. Phys Rev B, 2000, 61: 8233. doi: 10.1103/PhysRevB.61.8233
[87]	Siders C W, Cavalleri A, Sokolowski-Tinten K, et al. Detection of nonthermal melting by ultrafast X-ray diffraction[J]. Science, 1999, 286: 1340-1342. doi: 10.1126/science.286.5443.1340
[88]	Harb M, Ernstorfer R, Hebeisen C T, et al. Electronically driven structure changes of Si captured by femtosecond electron diffraction[J]. Phys Rev Lett, 2008, 100: 155504. doi: 10.1103/PhysRevLett.100.155504
[89]	Siwick B J, Dwyer J R, Jordan R E, et al. An atomic-level view of melting using femtosecond electron diffraction[J]. Science, 2003, 302(5649): 1382-1385. doi: 10.1126/science.1090052
[90]	Rousse A, Rischel C, Fourmaux S, et al. Non-thermal melting in semiconductors measured at femtosecond resolution[J]. Nature, 2001, 410: 65-68. doi: 10.1038/35065045
[91]	Lindenberg A M, Larsson J, Sokolowski-Tinten K, et al. Atomic-scale visualization of inertial dynamics[J]. Science, 2005, 308(5720): 392-395. doi: 10.1126/science.1107996
[92]	Mazevet S, Clerouin J, Recoules V, et al. Ab initio simulations of the optical properties of warm dense gold[J]. Phys Rev Lett, 2005, 95: 085002. doi: 10.1103/PhysRevLett.95.085002
[93]	Xu B, Hu S X. Effects of electron-ion temperature equilibrium on inertial confinement fusion implosions[J]. Phys Rev E, 2011, 84: 016408. doi: 10.1103/PhysRevE.84.016408
[94]	Landau L D. Kinetic equation for the Coulomb effect[J]. Zh Eksp Teor Fiz, 1937, 7: 203.
[95]	Spitzer L. Physics of fully ionized gases[M]. New York: Interscience, 1967.
[96]	Gericke D O, Murillo M S, Schlanges M. Dense plasma temperature equilibration in the binary collision approximation[J]. Phys Rev E, 2002, 65: 036418. doi: 10.1103/PhysRevE.65.036418
[97]	Brown L S, Preston D L, Singleton R L. Electron-ion energy partition when a charged particle slows in a plasma: Results[J]. Phys Rev E, 2012, 86: 016406. doi: 10.1103/PhysRevE.86.016406
[98]	Glosli J N, Graziani R R, More R M, et al. Molecular dynamics simulations of temperature equilibration in dense hydrogen[J]. Phys Rev E, 2008, 78: 025401. doi: 10.1103/PhysRevE.78.025401
[99]	Falk K, Collins L A, Gambo E J, et al. Combined X-ray scattering, radiography, and velocity interferometry/streaked optical pyrometry measurements of warm dense carbon using a novel technique of shock-and-release[J]. Phys Plasmas, 2014, 21: 056309. doi: 10.1063/1.4876613
[100]	Widmann K, Ao T, Foord M E, et al. Single-state measurement of electrical conductivity of warm dense gold[J]. Phys Rev Lett, 2004, 92: 125002. doi: 10.1103/PhysRevLett.92.125002
[101]	Ao T, Ping Y, Widmann K, et al. Optical properties in nonequilibrium phase transitions[J]. Phys Rev Lett, 2006, 96: 055001. doi: 10.1103/PhysRevLett.96.055001
[102]	Chen Z, Sametoglu V, Tsui Y Y, et al. Flux-limited nonequilibrium electron energy transport in warm dense gold[J]. Phys Rev Lett, 2012, 108: 165001. doi: 10.1103/PhysRevLett.108.165001
[103]	Chen Z, Holst B, Kirkwood S E, et al. Evolution of ac conductivity in nonequilibrium warm dense gold[J]. Phys Rev Lett, 2013, 110: 135001. doi: 10.1103/PhysRevLett.110.135001
[104]	Kubo R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems[J]. J Phys Soc Jpn, 1957, 12: 570-586. doi: 10.1143/JPSJ.12.570
[105]	Greenwood D A. The Boltzmann equation in the theory of electrical conduction in metals[J]. Proc Phys Soc London, 1958, 71: 585-596. doi: 10.1088/0370-1328/71/4/306
[106]	Witte B B L, Fletcher L B, Galtier E, et al. Warm dense matter demonstrating non-Drude conductivity from observations of nonlinear plasmon damping[J]. Phys Rev Lett, 2017, 118: 225001. doi: 10.1103/PhysRevLett.118.225001
[107]	Lu Binbin, Kang Dongdong, Wang Dan, et al. Towards the same line of liquid-liquid phase transition of dense hydrogen from various theoretical predictions[J]. Chin Phys Lett, 2019, 36: 103102. doi: 10.1088/0256-307X/36/10/103102
[108]	Ma Qian, Kang Dongdong, Zhao Zengxiu, et al. Directly calculated electrical conductivity of hot dense hydrogen from molecular dynamics simulation beyond Kubo-Greenwood formula[J]. Phys Plasmas, 2018, 25: 012707. doi: 10.1063/1.5013631
[109]	Glenzer S H, Redmer R. X-ray Thomson scattering in high energy density plasmas[J]. Rev Mod Phys, 2009, 81: 1625. doi: 10.1103/RevModPhys.81.1625
[110]	Baczewski A D, Shulenburger L, Desjarlais M P, et al. X-ray Thomson scattering in warm dense matter without the Chihara decomposition[J]. Phys Rev Lett, 2016, 116: 115004. doi: 10.1103/PhysRevLett.116.115004
[111]	Chihara J. Interaction of photons with plasmas and liquid metals—photoabsorption and scattering[J]. J Phys: Condens Matter, 2000, 12: 231. doi: 10.1088/0953-8984/12/3/303