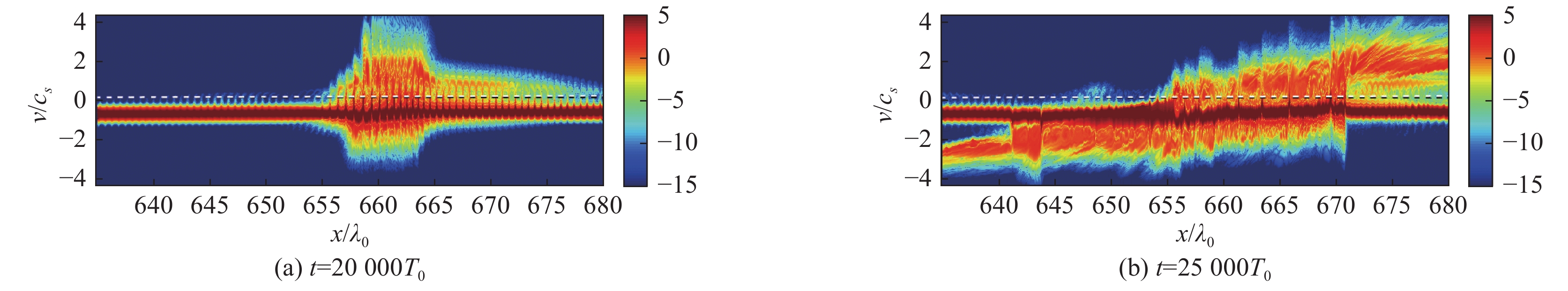Nonlinear enhancement and saturation of stimulated Brillouin scattering
-
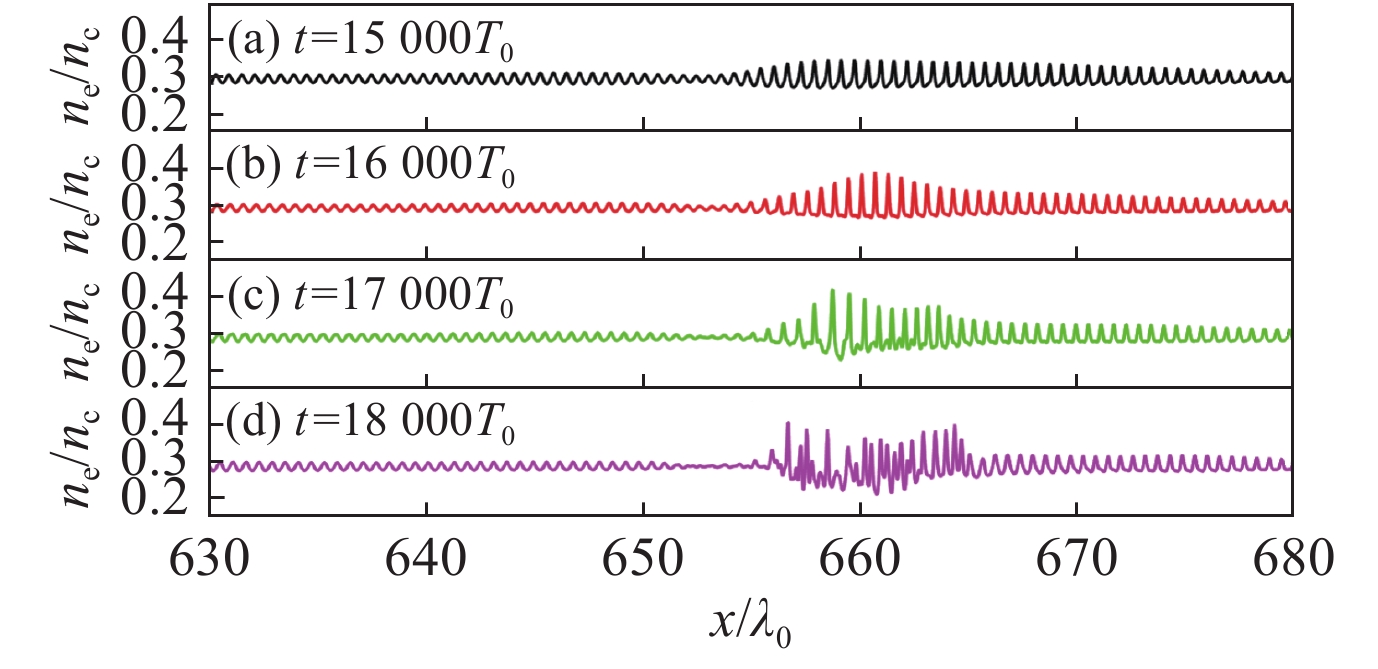
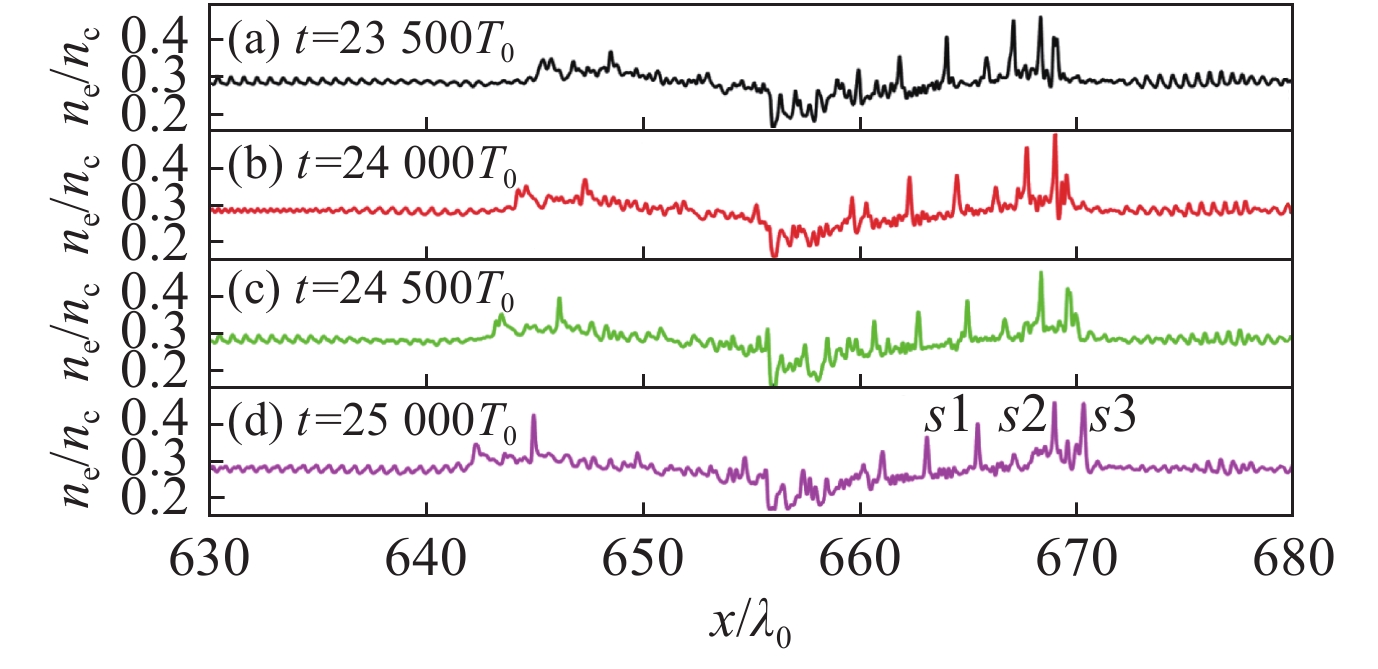
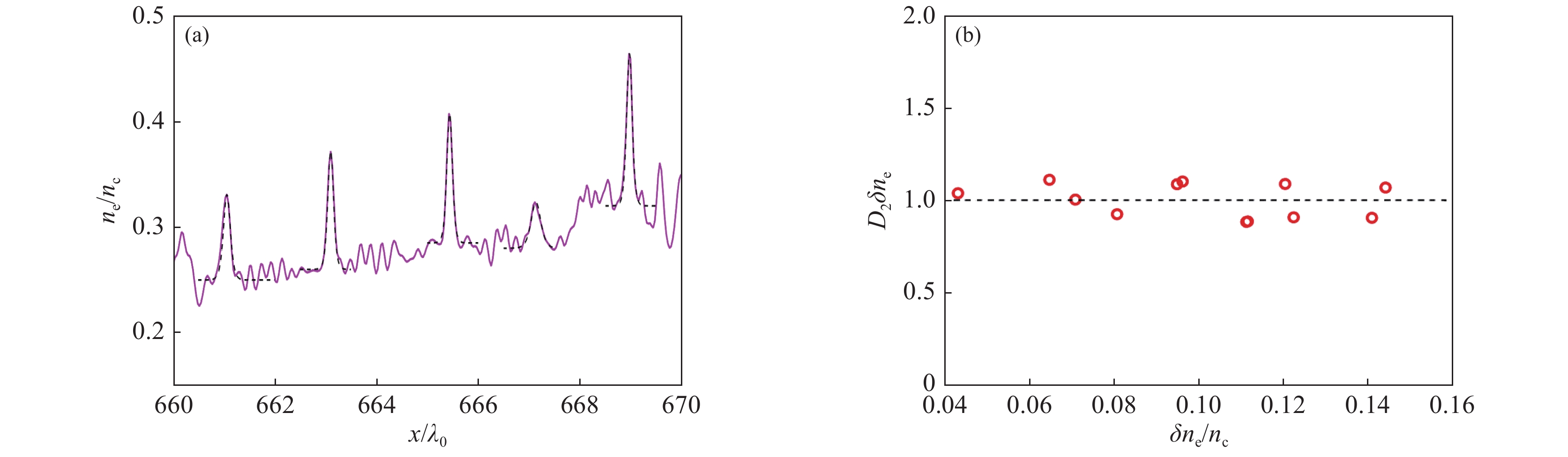
摘要: 针对典型激光聚变等离子体参数条件，利用弗拉索夫程序研究非均匀流等离子体中受激布里渊散射的非线性行为。在动理学效应占主导的参数区域，观察到受激布里渊散射激发的离子声波由于非线性动理学频移和非均匀流空间失谐相互补偿引起的离子声波自共振增长，这会导致受激布里渊水平量级的增强；提出用光束时间去相干抑制这种绝对增长。在流体非线性占主导的参数区域，观察到由于离子声波谐波导致的孤立波产生、离子加热以及受激布里渊散射饱和现象。Abstract: The nonlinear evolution of stimulated Brillouin scattering (SBS) in inhomogeneous flowing plasmas is self-consistently investigated by the Vlasov-Maxwell simulations. In the physical regime where ion trapping is dominant, simulations show that the evolution of SBS includes a linear convective stage and a nonlinear stage. In the linear stage, the reflectivity is in good agreement with the theoretical prediction from the Rosenbluth gain. In the nonlinear stage, the reflectivity shows a continuous increase and becomes much larger than the theoretical value. And the auto-resonant growing of ion acoustic wave (IAW) shows a nature of absolute instability, which can be explained as the compensation of the negative kinetic frequency shift from trapped ions and the detuning due to the flow velocity gradient. Methods using the incoherence in the pump waves to mitigate the enhanced SBS are proposed. The saturation of SBS by the decay to solitary turbulence of the IAW is demonstrated in the fluid dominant regime. The formation of solitary structures is due to the generation of harmonics of IAW.
-
图 1 （a）正负梯度流中SBS反射率随时间变化；（b）SBS反射率随激光强度的变化
Figure 1. （a）SBS reflectivity for both the positive flow gradient（blue solid line）and the negative flow gradient（red dashed-dotted line）;（b）Average reflectivity in the positive flow gradient and the negative flow gradient as a function of laser intensity:
${R_{{\rm{1,ave}}}}$ is the average value in the linear convective stage and${R_{{\rm{2,ave}}}}$ is the average value in the nonlinear stage. Black dashed lines show the reflectivity predicted by Rosenbluth gain
图 2 （a）正负梯度下离子分布函数以及（b）不同时刻离子声波振幅的空间演化
Figure 2. Spatial evolution of ion acoustic waves （IAWs） in the positive flow gradient（a）and in the negative flow gradient（b）
图 3 受激布里渊散射平均反射率随泵浦激光偏振方向旋转频率的变化关系
Figure 3. Average reflectivity of SBS versus polarization rotation frequency
图 4 不同时刻离子声波的密度扰动的空间演化
Figure 4. Spatial evolution of ion acoustic wave at different time
图 5 不同时刻离子声波的密度扰动的空间演化，显示孤立子的形成
Figure 5. Spatial evolution of ion acoustic wave at different time
图 6 （a）孤立子的空间分布，（b）孤立子的宽度与振幅的关系
Figure 6. （a）Spatial distribution of solitary structures;（b）Relation of width with amplitude of solitary structures
-
下载:
点击查看大图
计量
- 文章访问数: 1434
- HTML全文浏览量: 239
- PDF下载量: 100
- 被引次数: 0
