Introduction of laboratory astrophysics with intense lasers
-
摘要: 实验室天体物理是交叉于高能量密度等离子体物理学与天体物理学之间的一个新的学科生长点。利用强激光装置可以在实验室创造与某些天体或天体周围相似的极端物理环境,这样的实验条件前所未有,且与天体物理中诸多重要的物理现象直接对应。通过近距、主动、参数可控的研究,实验室天体物理有助于解决目前天体物理和等离子体物理中的一些关键的、共性的问题,并有望取得突破性成果。针对近年来国内外在该领域取得的最新研究进展进行介绍,并就将来可能开展的研究方向进行展望。Abstract: Laboratory astrophysics came into being with the advent of modern high-energy density physics research devices that can be used to create extreme physical conditions in the laboratory similar to those of certain celestial bodies or their surroundings, such as high-power lasers or pinch devices to generate extreme astrophysical plasma conditions. Such experimental conditions are unprecedented and correspond directly to many important and critical physical phenomena in astrophysics. They enable people to study the problems with astrophysical background in the laboratory in a close, active and controllable way. This paper introduces the latest progress in this field in recent years, and presents perspectives on future research directions.
-
Key words:
- laboratory astrophysics /
- intense lasers /
- magnetic reconnection /
- opacity /
- jet
-
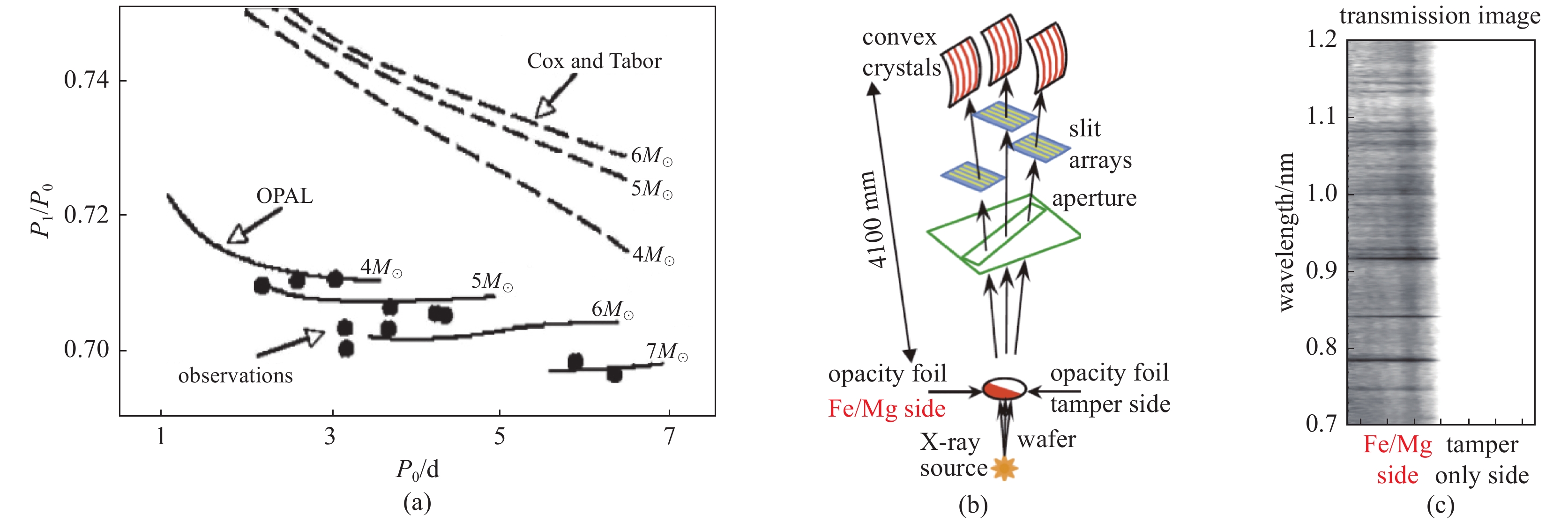
图 1 (a)双模造父变星的前两个谐波周期的比值与恒星质量的关系。黑色圆圈表示观测值。黑色虚线为Cox 和 Tabor[13]使用旧的不透明度计算得到的周期。黑色实线为使用实验标定后OPAL-DTA模型得到的周期。M☉是太阳质量,P0是基模周期,P1是第一谐变周期。(b)Bailey等人实验的布置图[25]。(c)Bailey等人实验中得到的空间和光谱分辨的透过率的图。暗色的区域对应于高吸收,白色区域对应于100%的透过率[25]
Figure 1. (a)Diagram of the ratio of the first two harmonics periods of double-mode Cepheid variable star. Circles represent observations. The upper set of three (dashed) curves correspond to the simulated result using older opacities,which ignore the full fine structure of the metals and calculated by Cox and Tabor[13]. The lower (solid) curves correspond to simulations with OPAL-DTA. M☉ is the solar mass,P0 is the fundamental mode period and P1 is the first overtone period. (b) Experimental setup of Bailey et al 2015[25]. (c) A spatially resolved and spectrally resolved transmission image obtained by Bailey et al 2015. Darker regions correspond to higher absorption. The white portion of the image corresponds to 100% transmission[25].
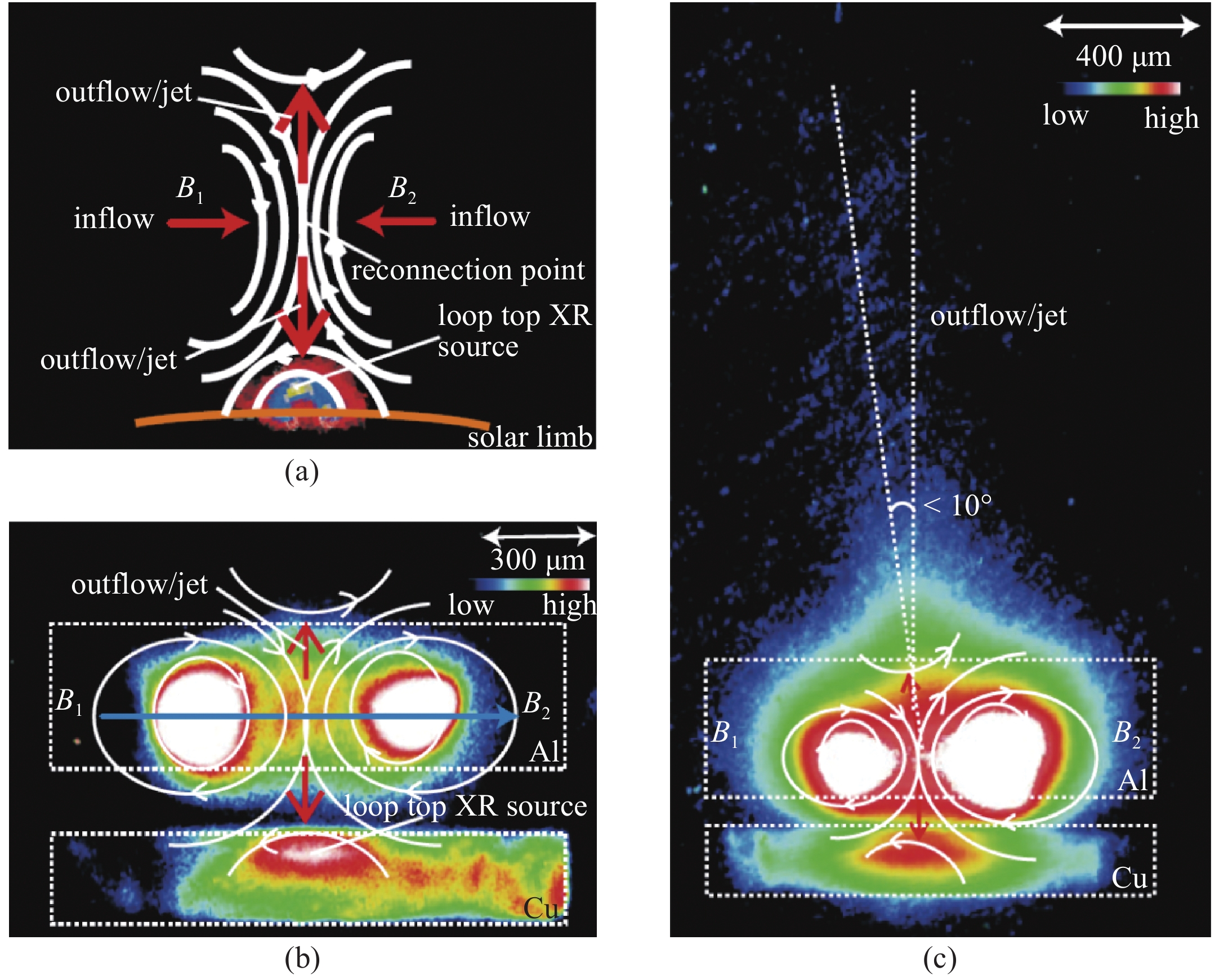
图 6 (a)磁场分布以及环顶X射线源的示意图。(b)靶前的针孔相机拍摄的X射线结果。(c)不对称激光强度导致激光光斑以及磁场B1和B2的不平衡的X射线结果[5]
Figure 6. (a) Magnetic reconnection model for the loop-top X-ray source in a compact solar flare,with a sketch depicting the X-ray observation scheme. (b) The pinhole X-ray image observed forward of the Al foil target. (c) The pinhole X-ray result of unbalanced laser intensity leading to laser spot and unbalanced magnetic fields B1 and B2[5]
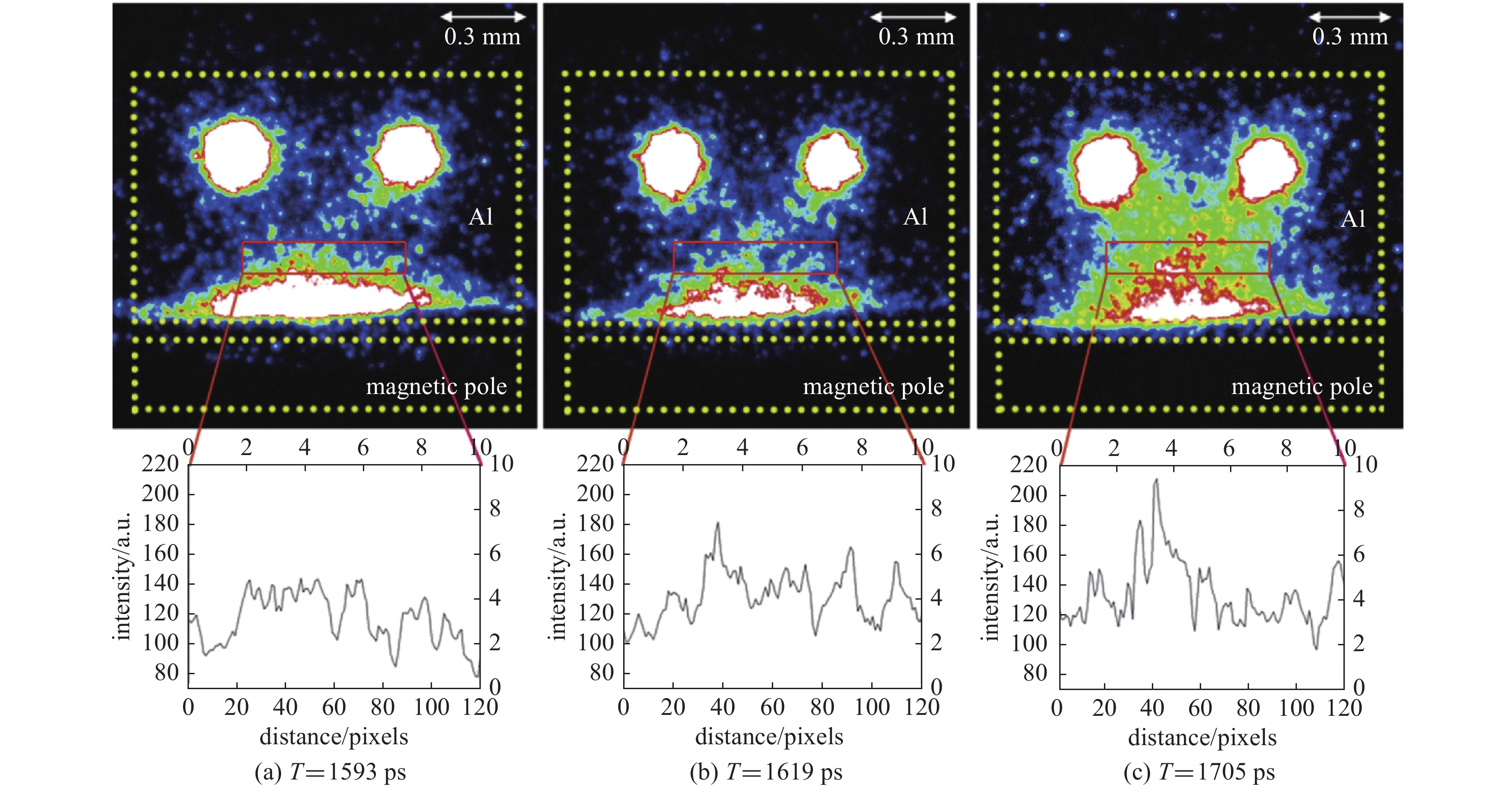
图 12 (a)无外加磁场为零,(b)外加磁场是0.4 T。(a)和(b)是实验中阴影图的图像,(c)和(d)是对比增强数据,(e)~(h)表示外加0.4 T磁场时,在不同时刻,KHI演化区域的磁场分布图[73]
Figure 12. (a) The magnetic field of a magnet was null. (b) the magnetic field was 0.4 T. (a) and (b) are images from the shadowgraphs in the experiments,and (c) and (d) are contrast-enhanced data. (e)~(h) The distribution of magnetic field in the evolution region of KHI during 0~9 ns[73]
research topic same physics similar physics relative physics laser plasma interaction collision between molecular clouds particle transport non-local transport of neutrino in young neutron star hydrodynamics and shocks equation of state (giant planet) interaction of molecular cloud with strong shock wave generated in supernovae remnant:solar flare,solar wind in solar-terrestrial space,generation and collimation of jet collisionless shock and particle acceleration (origin of cosmic rays) hydrodynamics instabilities generation and amplification of magnetic field Rayleigh-Taylor instability during supernovae explosion;Kelvin-Helmholtz instability during the interaction between solar wind and earth’s magnetic field hydrodynamics instabilities during neutrino driven supernovae explosion;Rayleigh-Taylor instability in planetary nebula atomic physics and X-ray transport opacity (stellar evolution) non-local thermodynamic equilibrium (non-LTE) plasma spectroscopy non-LTE atomic physics in supernovae remnant;stellar jets (non-relativistic) radiation hydrodynamics in early galaxy;photoionized plasma X-ray laser in the universe laser-produced relativistic plasma fireball model of gamma-ray bursts;cosmological jets length/cm time/s pressure/Pa density/cm−3 velocity/(km·s−1) magnetic field/T flare plasmas 109 ~ 1010 100 ~ 1000 0.001 ~ 10 109 ~ 1011 10 ~ 100 10−3 ~ 10−2 laser-produced plasmas ~10−1 ~10−9 ~107 1019 ~ 1020 ~100 ~102 flare plasmas (scaled) 10−2~ 10−1 10−10 ~10−9 107 ~ 1011 1019 ~ 1021 100 ~ 1000 102 ~ 103 表 3 光致电离等离子体中重要的原子过程
Table 3. Atomic transitions in photoionized plasmas
direct process inverse process radiative decay(A) photoexcitation(PE) photoionization(PI) radiative recombination(RR) collisional excitation(CE) collisional deexcitation(CD) collisional ionization(CI) three-body recombination(TR) autoionization(AI) dielectronic capture(DC) -
[1] Drake R P. Introduction to high-energy-density physics[M]. Berlin Heidelberg: Springer, 2006. [2] Rogers F J, Iglesias C A. Astrophysical opacity[J]. Science, 1994, 263(5143): 50-55. doi: 10.1126/science.263.5143.50 [3] Pound M W. Scaled eagle nebula experiments on NIF[R/OL]. http://www.osti.gov/scitech/biblio/1348848. [4] Grosskopf M Y, Drake R P, Miles A R, et al. Modeling of aspheric, diverging hydrodynamic instability experiments on the National Ignition Facility[J]. High Energy Dens Phys, 2013, 9: 439-447. doi: 10.1016/j.hedp.2013.04.003 [5] Zhong J, Li Y, Wang X, et al. Modelling loop-top X-ray source and reconnection outflows in solar flares with intense lasers[J]. Nature Physics, 2010, 6: 984. doi: 10.1038/nphys1790 [6] Casey D T, Sayre D B, Brune C R, et al. Thermonuclear reactions probed at stellar-core conditions with laser-based inertial-confinement fusion[J]. Nature Physics, 2017, 13(12): 1227. doi: 10.1038/nphys4220 [7] Remington B A, Drake R P, Ryutov D D, et al. Experimental astrophysics with high power lasers and Z pinches[J]. Reviews of Modern Physics, 2006, 78(3): 755-807. doi: 10.1103/RevModPhys.78.755 [8] Lebedev S V, Frank A, Ryutov D D. Exploring astrophysics-relevant magnetohydrodynamics with pulsed-power laboratory facilities[J]. Review of Modern Physics, 2019, 91: 025002. doi: 10.1103/RevModPhys.91.025002 [9] Takabe H. Astrophysics with intense and ultra-intense lasers laser "astrophysics"[J]. Progress of Theoretical Physics Supplements, 2001, 143: 202. doi: 10.1143/PTPS.143.202 [10] Hansen C J, Kawaler S D, Trimble V. Stellar interiors: physical principles, structure, and evolution [M]. 2nd ed. New York: Springer, 2004, . [11] 王菲鹿, 赵刚, 张杰. 天体辐射不透明度的实验室研究[J]. 物理, 2002, 31(5):298-301. (Wang Feilu, Zhao Gang, Zhang Jie. Laboratory studies of astrophysical opacity[J]. Physics, 2002, 31(5): 298-301 doi: 10.3321/j.issn:0379-4148.2002.05.008 [12] Remington B A, Arnett D, Drake P, et al. Modeling astrophysical phenomena in the laboratory with intense lasers[J]. Science, 1999, 284: 1488-1493. doi: 10.1126/science.284.5419.1488 [13] Cox A N, Tabor J E. Radiative opacity tables for 40 stellar mixtures[J]. The Astrophysical Journal Supplement, 1976, 31: 271-312. doi: 10.1086/190383 [14] Da Silva L B, MacGowan B J, Kania D R, et al. Absorption measurements demonstrating the importance of <italic>n</italic>=0 transitions in the opacity of iron[J]. Phys Rev Lett, 1992, 69: 438-441. doi: 10.1103/PhysRevLett.69.438 [15] Springer P T, Fields D J, Wilson B G, et al. Spectroscopic absorption measurements of an iron plasma[J]. Phys Rev Lett, 1992, 69: 3735-3738. doi: 10.1103/PhysRevLett.69.3735 [16] Iglesias C A, Rogers F J. Opacity tables for cepheid variables[J]. The Astrophysical Journal Letters, 1991, 371: L73-L75. doi: 10.1086/186005 [17] Rogers F J, Iglesias, C A. Radiative atomic Rosseland mean opacity tables[J]. The Astrophysical Journal Supplement, 1992, 79: 507-568. doi: 10.1086/191659 [18] Delahaye F, Pinsonneault M. Comparison of radiative accelerations obtained with atomic data from OP and OPAL[J]. The Astrophysical Journal Supplement, 2005, 625: 563-575. doi: 10.1086/429583 [19] Asplund M, Grevesse N, Sauval J A, et al. The chemical composition of the Sun[J]. Annu. Rev. Astronomy Astrophysics, 2009, 47: 481-22. doi: 10.1146/annurev.astro.46.060407.145222 [20] Caffau E, Ludwig H G, Steffen M. Solar chemical abundances determined with a CO5BOLD 3D model atmosphere[J]. Solar Physics, 2011, 268: 255-269. doi: 10.1007/s11207-010-9541-4 [21] Basu S, Antia H M. Helioseismology and solar abundances[J]. Physics Reports, 2008, 457: 217-283. doi: 10.1016/j.physrep.2007.12.002 [22] Basu S, Grevesse N, Mathis S, et al. Understanding the internal chemical composition and physical processes of the solar interior[J]. Space Science Reviews, 2014, 196: 49-77. [23] Bahcall J N, Serenelli A M, Pinsonneault M. How accurately can we calculate the depth of the solar convective zone[J]. Astrophys J, 2004, 614: 464-471. doi: 10.1086/423027 [24] Serenelli A M, Basu S, Ferguson J W, et al. New solar composition: the problem with solar models revisited[J]. Astrophys J, 2009, 705: L123-L127. doi: 10.1088/0004-637X/705/2/L123 [25] Bailey J E, Nagayama T, Loisel G P, et al. A higher-than-predicted measurement of iron opacity at solar interior temperatures[J]. Nature, 2015, 517: 56-59. doi: 10.1038/nature14048 [26] Zweibel E. The seeds of a magnetic universe[J]. Physics, 2013, 6: 85. [27] Gregori G, Ravasio A, Murphy C D, et al. Generation of scaled protogalactic seed magnetic fields in laser-produced shock waves[J]. Nature, 2012, 481: 480-483. doi: 10.1038/nature10747 [28] Zhong J, Yuan X, Han B, et al. Magnetic reconnection driven by intense lasers[J]. High Power Laser Science & Engineering, 2018, 6(3): 89-105. [29] Warren J S, Hughes J P, Badenes C, et al. Cosmic-ray acceleration at the forward shock in Tycho's supernova remnant: Evidence from Chandra X-ray observations[J]. Astrophys J, 2005, 634: 376. doi: 10.1086/496941 [30] Fiore M, Silva L O, Ren C, et al. Baryon loading and the Weibel instability in gamma-ray bursts[J]. Mon Not R Astron Soc, 2006, 372: 1851. doi: 10.1111/j.1365-2966.2006.10980.x [31] Weibel E S. Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution[J]. Phys Rev Lett, 1959, 2(3): 83. doi: 10.1103/PhysRevLett.2.83 [32] Fried B D. Mechanism for instability of transverse plasma waves[J]. Phys Fluids, 1959, 2: 337. [33] Huntington C M, Fiuza F, Ross J S, et al. Observation of magnetic field generation via the Weibel instability in interpenetrating plasma flows[J]. Nature Physics, 2013, 11(2): 173-176. [34] Okada T, Ogawa K. Saturated magnetic field for Weibel instability in ultra intense laser-plasma interactions[J]. Journal of Plasma Physics, 2007, 14: 072702. doi: 10.1063/1.2746023 [35] Meinecke J, Doyle H W, Miniati F, et al. Turbulent amplification of magnetic fields in laboratory laser-produced shock waves[J]. Nature Physics, 2014, 10(7): 520-524. doi: 10.1038/nphys2978 [36] Ryutov D, Drake R P, Kane J, et al. Similarity criteria for the laboratory simulation of supernova hydrodynamics[J]. The Astrophysical Journal, 1999, 518(2): 821-832. doi: 10.1086/307293 [37] RyutovD, Drake RP, Remington B A. Criteria for scaled laboratory simulations of astrophysical MHD phenomena[J]. The Astrophysical Journal Supplement Series, 2000, 127(2): 465-468. doi: 10.1086/313320 [38] RyutovD, Remington B A, Robey H F, et al. Magnetohydrodynamic scaling: From astrophysics to the laboratory[J]. Physics of Plasmas, 2001, 8(5): 1804-1816. doi: 10.1063/1.1344562 [39] Bouquet S, Falize E, Michaut C, et al. From lasers to the universe: scaling laws in laboratory astrophysics[J]. High Energy Density Physics, 2010, 6(4): 368-380. doi: 10.1016/j.hedp.2010.03.001 [40] Falize E, Michaut C, Bouquet S. Similarity properties and scaling laws of radiation hydrodynamic flows in laboratory astrophysics[J]. The Astrophysical Journal, 2011, 730(2): 96-102. doi: 10.1088/0004-637X/730/2/96 [41] Ryutov D, Remington B A. Similarity laws for collisionless interaction of superstrong electromagnetic fields with a plasma[J]. Plasma Physics and Controlled Fusion, 2006, 48(3): L23-L31. doi: 10.1088/0741-3335/48/3/L01 [42] Ryutov D, Remington B A. Scaling laws for collisionless laser-plasma interactions of relevance to laboratory astrophysics[J]. Astrophysics and Space Science, 2007, 307(1/3): 291-296. [43] Remington B A, Drake R P, Takabe H, et al. A review of astrophysics experiments on intense lasers[J]. Physics of Plasmas, 2000, 7(5): 1641-1652. doi: 10.1063/1.874046 [44] Li C K, Tzeferacos P, Lamb D, et al. Scaled laboratory experiments explain the kink behaviour of the Crab Nebula jet[J]. Nature Communications, 2016, 7: 13081. doi: 10.1038/ncomms13081 [45] Golub L, Bookbinder J, Deluca E, et al. A new view of the solar corona from the transition region and coronal explorer (TRACE)[J]. Phys Plasmas, 1991, 6(5): 2205-2216. [46] Loureiro N, Uzdensky D A. Magnetic reconnection: from the Sweet-Parker model to stochastic plasmoid chains[J]. Plasma Phys Control Fusion, 2016, 58: 014021. doi: 10.1088/0741-3335/58/1/014021 [47] Masuda S, Kosugi T, Hara H, et al. A loop-top hard X-ray source in a compact solar flare as evidence for magnetic reconnection[J]. Nat Phys, 1994, 371(6497): 495-497. doi: 10.1038/371495a0 [48] Willingale L, Nilson P M, Kaluza M C, et al. Proton deflectometry of a magnetic reconnection geometry[J]. Phys Plasmas, 2010, 17: 043104. doi: 10.1063/1.3377787 [49] Nilson P M, Willingale L, Kaluza M C, et al. Bidirectinal jet formation during driven magnetic reconnection in two-beam laser-plasma interactions[J]. Phys Plasmas, 2008, 15: 092701. doi: 10.1063/1.2966115 [50] Nilson P M, Willingale L, Kaluza M C, et al. magnetic reconnection and plasma dynamics in two-beam laser-solid interactions[J]. Phys Rev Lett, 2006, 97: 255001. [51] Li C K, Seguin F H, Frenje J A, et al. Observation of megagauss field topology changes due to magnetic reconnection in laser-produced plasmas[J]. Phys Rev Lett, 2007, 99: 055001. [52] Fiksel G, Fox W, Bhattacharjee A, et al. Magnetic reconnection between colliding magnetized laser-produced plasma plumes[J]. Phys Rev Lett, 2014, 113: 105003. [53] 李彦霏, 李玉同. 强激光实验室天体物理研究进展[J]. 物理, 2016, 45(2):80-87. (Li Yanfei, Li Yutong. Recent progress of high-power laser driven laboratory astrophysics[J]. Physics, 2016, 45(2): 80-87 doi: 10.7693/wl20160202 [54] Brady P, Ditmire T, Horton W, et al. Laboratory experiments simulating solar wind driven magnetospheres[J]. Physice of Plasmas, 2009, 16: 043112. doi: 10.1063/1.3085786 [55] Zhang K, Zhong J Y, Wang J Q, et al. Modeling the interaction of solar wind with a dipole magnetic field with Shenguang II intense lasers[J]. High Energy Density Physics, 2015, 17: 32-37. doi: 10.1016/j.hedp.2014.11.001 [56] Katsukawa Y, Berger T E, Ichimoto K, et al. Small-scale jetlike features in penumbral chromospheres[J]. Science, 2007, V318: 1594-1596. [57] Blandford R D, Znajek R L. Electromagnetic extraction of energy from Kerr black holes[J]. Monthly Notices of the Royal Astronomical Society, 1977, 179: 433-456. doi: 10.1093/mnras/179.3.433 [58] Blandford R D, Payne D G. Hydromagnetic flows from accretion disks and the production of radio jets[J]. Monthly Notices of the Royal Astronomical Society, 1982, 199: 883-903. doi: 10.1093/mnras/199.4.883 [59] Gao L, Liang E, Lu Y, et al. Mega-gauss plasma jet creation using a ring of laser beams[J]. Astrophys J Lett, 2019, 873: L11. doi: 10.3847/2041-8213/ab07bd [60] Lu Y, Tzeferacos P, Liang E, et al. Numerical simulation of magnetized jet creation using a hollow ring of laser beams[J]. Phys Plasmas, 2019, 26: 022902. doi: 10.1063/1.5050924 [61] Albertazzi B, Ciardi A, Nakatsutsumi M, et al. Laboratory formation of a scaled protostellar jet by coaligned poloidal magnetic field[J]. Science, 2014, 346: 325-328. doi: 10.1126/science.1259694 [62] 王敏. 大尺度赫比格-哈罗天体的光学研究进展[J]. 天文学进展, 2002, 20(1):59-73. (Wang Min. Progress in optical studies on parsec-scale Herbig-Haro flows[J]. Progress in Astronomy, 2002, 20(1): 59-73 doi: 10.3969/j.issn.1000-8349.2002.01.006 [63] 王红池. 赫比格-哈罗天体高分辨观测研究进展[J]. 天文学进展, 2000, 18(3):216-228. (Wang Hongchi. Progress in observational studies with high spatial resolution on Herbig-Haro objects[J]. Progeress in Astronomy, 2000, 18(3): 216-228 doi: 10.3969/j.issn.1000-8349.2000.03.004 [64] Kajdic P, Reipurth B, Raga A C, et al. Proper motions of the HH 110/270 system[J]. Astrophys J, 2012, 143: 106. [65] Yuan D W, Wu Junfeng, Li Yutong, et al. Modeling supersonic-jet deflection in the Herbig-Haro 110-270 system with high-power lasers[J]. Astrophys J, 2015, 815: 46. doi: 10.1088/0004-637X/815/1/46 [66] Remington B A. Experiments in ICF, materials science, and astrophysics[M]. Edward Teller Lectures: Lasers and Inertial Fusion Energy, 2013 [67] Kuranz C C, Park H S, Huntington C M, et al. How high energy fluxes may affect Rayleigh-Taylor instability growth in young supernova remnants[J]. Nature Communications, 2018, 9(1): 1564. doi: 10.1038/s41467-018-03548-7 [68] Gómez, Daniel O, Deluca E E, Mininni P D. Simulations of the Kelvin-Helmholtz instability driven by coronal mass ejections in the turbulent corona[J]. Astrophysical Journal, 2016, 818(2): 126. doi: 10.3847/0004-637X/818/2/126 [69] Price D J, Rosswog S. Producing ultrastrong magnetic fields in neutron star mergers[J]. Science, 2006, 312(5774): 719-722. doi: 10.1126/science.1125201 [70] Hasegawa H, Fujimoto M, Phan T D, et al. Transport of solar wind into Earth's magnetosphere through rolled-up Kelvin-Helmholtz vortices[J]. Nature, 2004, 430(7001): 755-758. doi: 10.1038/nature02799 [71] Wan W C, Malamud G, Shimony A, et al. Observation of single-mode, Kelvin-Helmholtz instability in a supersonic flow[J]. Phys Rev Lett, 2015, 115: 145001. [72] Sun W, Zhong J Y, Zhang S, et al. The effect on the linear stage evolution of Kelvin-Helmholtz instability with external magnetic field[J]. High Energy Dens Phys, 2019, 31: 47-51. doi: 10.1016/j.hedp.2019.02.003 [73] Sun W, Zhong J Y, Lei Z, et al. Suppressing Kelvin-Helmholtz instability with an external magnetic field[J]. Plasma Phys Control Fusion, 2020, 60: 065007. [74] Ferland G, Savin D W. Spectroscopic challenges of photoionized plasmas[J]. Publications of the Astronomical Society of the Pacific, 2001, 113: 1024-024. doi: 10.1086/322922 [75] Han Bo, Wang Feilu, Salzmann D, et al. Modeling non-local thermodynamic equilibrium plasma using the Flexible Atomic Code data[J]. Publications of the Astronomical Society of Japan, 2015, 67: 29. [76] 韩波, 王菲鹿, 梁贵云, 等. 实验室光致电离等离子体中激发过程的研究[J]. 物理学报, 2016, 65:110503. (Han Bo, Wang FeiLu, Liang Guiyun, et al. Excitation processes in experimental photoionized plasmas[J]. Acta Physica Sinica, 2016, 65: 110503 doi: 10.7498/aps.65.110503 [77] Foord M E. Charge-state distribution and Doppler effect in an expanding photoionized plasma[J]. Phys Rev Lett, 2004, 93: 055002. [78] Shinsuke F, Hideaki T, Norimasa Y, et al. X-ray astronomy in the laboratory with a miniature compact object produced by laser-driven implosion[J]. Nature Physics, 2009, 5: 821. doi: 10.1038/nphys1402 [79] Wang Feilu, Salzmann D, Zhao Gang, et al. Time-dependent simulation of photoionized plasma created by laboratory blackbody radiator[J]. The Astrophysical Journal, 2009, 706: 592-598. doi: 10.1088/0004-637X/706/1/592 [80] Edward H, Steven R. Photoionized astrophysical plasmas in the laboratory[J]. Physics of Plasma, 2010, 17: 103301. doi: 10.1063/1.3484225 [81] Bao Lihua, Wu Zeqing, Duan Bin, et al. Simulations of the spectrum from a photoionized Si plasma[J]. Physics of Plasma, 2011, 18: 023301. doi: 10.1063/1.3551737 [82] Wu Zeqing, Duan Bin, Li Yueming, et al. Time-dependent simulation of the spectrum from a photoionized Si plasma[J]. High Energy Density Physics, 2017, 23: 153-158. doi: 10.1016/j.hedp.2017.04.006 [83] Loisel G P, Bailey D A, Liedahl D A, et al. Benchmark experiment for photoionized plasma emission from accretion-powered X-ray sources[J]. Phys Rev Lett, 2017, 119: 075001. doi: 10.1103/PhysRevLett.119.075001 [84] White S, Irwin R, Warwick J R, et al. Production of photoionized plasmas in the laboratory with X-ray line radiation[J]. Physical Review E, 2018, 97: 063203. doi: 10.1103/PhysRevE.97.063203 [85] Bailie D, Hyland C, Singh R L, et al. An investigation of the L-shell X-ray conversion efficiency for laser-irradiated tin foils[J]. Plasma Science and Technology, 2020, 22: 045201. doi: 10.1088/2058-6272/ab6188 [86] Kotera K, Olinto A V. The Astrophysics of ultrahigh-energy cosmic rays[J]. Annual Review of Astronomy & Astrophysics, 2011, 49(1): 119-153. [87] Fermi E. On the origin of the cosmic radiation[J]. Phys Rev, 1949, 75: 169-174. [88] Scholer M. Diffusive acceleration[M]. New York: John Wiley & Sons, 1985: 287. [89] Sarris E T, Van Allen J A. Effects of interplanetary shock waves on energetic charged particles[J]. Journal of Geophysical Research, 1974, 79(28): 4157-4173. doi: 10.1029/JA079i028p04157 [90] Fu H S, Xu Y, Vaivads A, et al. Super-efficient electron acceleration by an isolated magnetic reconnection[J]. Astrophysical Journal, 2019, 870(2): L22. doi: 10.3847/2041-8213/aafa75 [91] Hoshino M M. Stochastic particle acceleration in multiple magnetic islands during reconnection[J]. Phys Rev Lett, 2012, 108: 135003. doi: 10.1103/PhysRevLett.108.135003 [92] Egedal J, Daughton W, Le A. Large-scale electron acceleration by parallel electric fields during magnetic reconnection[J]. Nature Physics, 2012, 8(4): 321-324. doi: 10.1038/nphys2249 [93] Drake J F, Swisdak M, Che H, et al. Electron acceleration from contracting magnetic islands during reconnection[J]. Nature Physics, 2006, 443(7111): 553-556. doi: 10.1038/nature05116 [94] Zhong J Y, Lin J, Li Y T, et al. Relativistic electrons produced by reconnecting electric fields in a laser-driven bench-top solar flare[J]. Astrophys J Suppl Ser, 2016, 225: 30. doi: 10.3847/0067-0049/225/2/30 [95] Dennis B R. Solar flare hard X-ray observations[J]. Solar Physics, 1988, 118: 49-94. doi: 10.1007/BF00148588 [96] Klebesadel R W, Strong I B, Olson R A. Observations of gamma-ray bursts of cosmic origin[J]. The Astrophysical Journal, 1973, 182: L85-L88. doi: 10.1086/181225 [97] Metzger M R, Djorgovski S G, Kulkarni S R, et al. Spectral constraints on the redshift of the optical counterpart to the γ-ray burst of 8 May 1997[J]. Nature, 1997, 387(6636): 878-880. doi: 10.1038/43132 [98] Piran T. The physics of gamma-ray bursts[J]. Reviews of Modern Physics, 2004, 76(4): 1143. [99] Zhang B, Mészáros P. Gamma-ray bursts: progress, problems & prospects[J]. International Journal of Modern Physics A, 2004, 19(15): 2385-2472. doi: 10.1142/S0217751X0401746X [100] Lazzati D, Perna R, Morsony B J, et al. Late time afterglow observations reveal a collimated relativistic jet in the ejecta of the binary neutron star merger GW170817[J]. Phys Rev Lett, 2017, 120: 241103. [101] Beloborodov A M. Radiation front sweeping the ambient medium of gamma-ray bursts[J]. The Astrophysical Journal, 2002, 565(2): 808-828. doi: 10.1086/324195 [102] Alkofer R, Hecht M B, Roberts C D, et al. Pair creation and an X-ray free electron laser[J]. Phys Rev Lett, 2001, 87: 193902. doi: 10.1103/PhysRevLett.87.193902 [103] Cowan T E, Perry M D, Key M H, et al. High energy electrons, nuclear phenomena and heating in petawatt laser-solid experiments[J]. Laser and Particle Beams, 1999, 17(4): 773-783. doi: 10.1017/S0263034699174238 [104] Wilks S C, Chen H, Liang E, et al. Electron-positron plasmas created by ultra-intense laser pulses interacting with solid targets[J]. Astrophysics and Space Science, 2005, 298: 347-355. doi: 10.1007/s10509-005-3967-4 [105] Myatt J, Delettrez J A, Maximov A V, et al. Optimizing electron-positron pair production on kilojoule-class high-intensity lasers for the purpose of pair-plasma creation[J]. Physical Review E, 2009, 79: 066409. doi: 10.1103/PhysRevE.79.066409 -




 下载:
下载: