Study on X-ray line emission diffraction in inertial confinement fusion and its recent progress
-
摘要: 介绍了惯性约束聚变研究中X射线线谱诊断与各物理量之间关系，并对X射线晶体谱仪诊断方式及诊断原理进行了简要说明。针对不同类型诊断，介绍了常用不同类型衍射晶体的作用与原理。此外，介绍了最近开展的一种新型变锥面弯晶X射线诊断方法研究，此方法拥有高集光效率的同时，保证了后端接收装置的精巧耦合，减小了像差。以变锥面弯晶衍射特性研究为出发点，开发了一个X射线任意面型晶体衍射追迹仿真软件X-Chase，并以国内某大型激光装置类H、类He线的变锥面晶体诊断为例进行了计算演示，数值模拟结果显示了变锥面晶体具有很好的聚焦效果。Abstract: This paper introduces the relationship between X-ray line emission diagnosis and various physical quantities in the study of inertial confinement fusion, and briefly explains the diagnosis method and principle of X-ray crystal spectrometer. For different types of diagnosis, it introduces the functions and principles of different commonly used types of diffraction crystals. In addition, it introduces a new type of X-ray diagnostic method of multi-cone curved crystals, which has high light collection efficiency and at the same time ensures the delicate coupling of the back-end receiving device and reduces aberrations. Based on the study of the diffraction characteristics of the multi-cone curved crystal, X-Chase, an X-ray arbitrary surface crystal diffraction tracking simulation software, was developed. At the same time, the multi-cone crystal of H and He line emissions on the SG laser facility is utilized to demonstrate the code functions. The numerical simulation results show that the variable cone crystal has a good focusing ability.
-
[1] 温树槐, 丁永坤. 激光惯性约束聚变诊断学[M]. 北京: 国防工业出版社, 2012: 200-205.Wen Shuhuai, Ding Yongkun. Laser inertial confinement fusion diagnostics[M]. Beijing: National Defense Industry Press, 2012: 200-205 [2] Basov N G, Danilychev V A, Glotov E P. Theoretical investigation of promising methods of improving the energy characteristics of CW industrial electron-beam-controlled lasers[J]. Journal of Soviet Laser Research, 1984, 5: 647-666. [3] Nuckolls J, Wood L, Thiessen A, et al. Laser compression of matter to super-high densities: Thermonuclear (CTR) applications[J]. Nature, 1972, 239(5368): 139-142. doi: 10.1038/239139a0 [4] Lindl J D, Amendt P, Berger R L, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility[J]. Physics of Plasmas, 2004, 11(2): 339-491. doi: 10.1063/1.1578638 [5] Champeney D C, Fuoss R M. Fourier transforms and their physical applications[J]. Physics Today, 1973, 26(10): 57. doi: 10.1063/1.3128283 [6] James R W. The dynamical theory of X-ray diffraction[J]. Solid State Physics, 1963, 15: 53-220. doi: 10.1016/S0081-1947(08)60592-5 [7] Wittry D B, Barbi N C. X-ray crystal spectrometers and monochromators in microanalysis[J]. Microscopy and Microanalysis, 2001, 7(2): 124-141. doi: 10.1007/S100050010080 [8] Nielsen J A, McMorrow D. Elements of modern X-ray physics[M]. London: John Wiley & Sons, 2011: 207-230. [9] Sanchez del Rio M, Bernstorff S, Savoia A, et al. A conceptual model for ray tracing calculations with mosaic crystals[J]. Review of Scientific Instrument, 1992, 63: 932-935. doi: 10.1063/1.1143784 [10] Gambaccini M, Taibi A, Del Guerra A, et al. Small-field imaging properties of narrow energy band X-ray beams for mammography[C]// IEEE Nuclear Science Symposium and Medical Imaging Conference Record. 1995, 3: 1388-1391. [11] Sanchez del Rio M, Ferrero C, Mocella V. Computer simulation of bent perfect crystal diffraction profiles[C]//Proc of SPIE. 1997, 3151: 312-323. [12] Honkanen A P, Ferrero C, Guigayb J P, et al. A finite-element approach to dynamical diffraction problems in reflection geometry[J]. Journal of Applied Crystallography, 2018, 51: 514-525. doi: 10.1107/S1600576718001930 [13] Freund A K. Mosaic crystals monochromators for synchrotron radiation instrumentation[J]. Nucl Instr and Met, 1988, A266: 461-466. [14] Koppel L N. Active-recording X-ray crystal spectrometer for laser-induced plasmas[J]. Review of Scientific Instrument, 1976, 47: 1109-1112. doi: 10.1063/1.1134826 [15] Barnsley R, Peacock N J, Dunn J, et al. Versatile high resolution crystal spectrometer with X-ray charge coupled device detector[J]. Review of Scientific Instrument, 2003, 74: 2388-2397. doi: 10.1063/1.1533105 [16] Johansson T. A novel precise focusing X-ray Spectrometer[J]. Journal of Physics, 1993, 82(7/8): 507-528. [17] Yaakobi B, Turner R E, Schnopper H W, et al. Focusing X-ray spectrograph for laser fusion experiments[J]. Review of Scientific Instrument, 1979, 50: 1609-1611. doi: 10.1063/1.1135776 [18] Hall T A. A focusing X-ray crystal spectrograph[J]. Journal of Physics E Scientific Instruments, 2000, 17(2): 110. 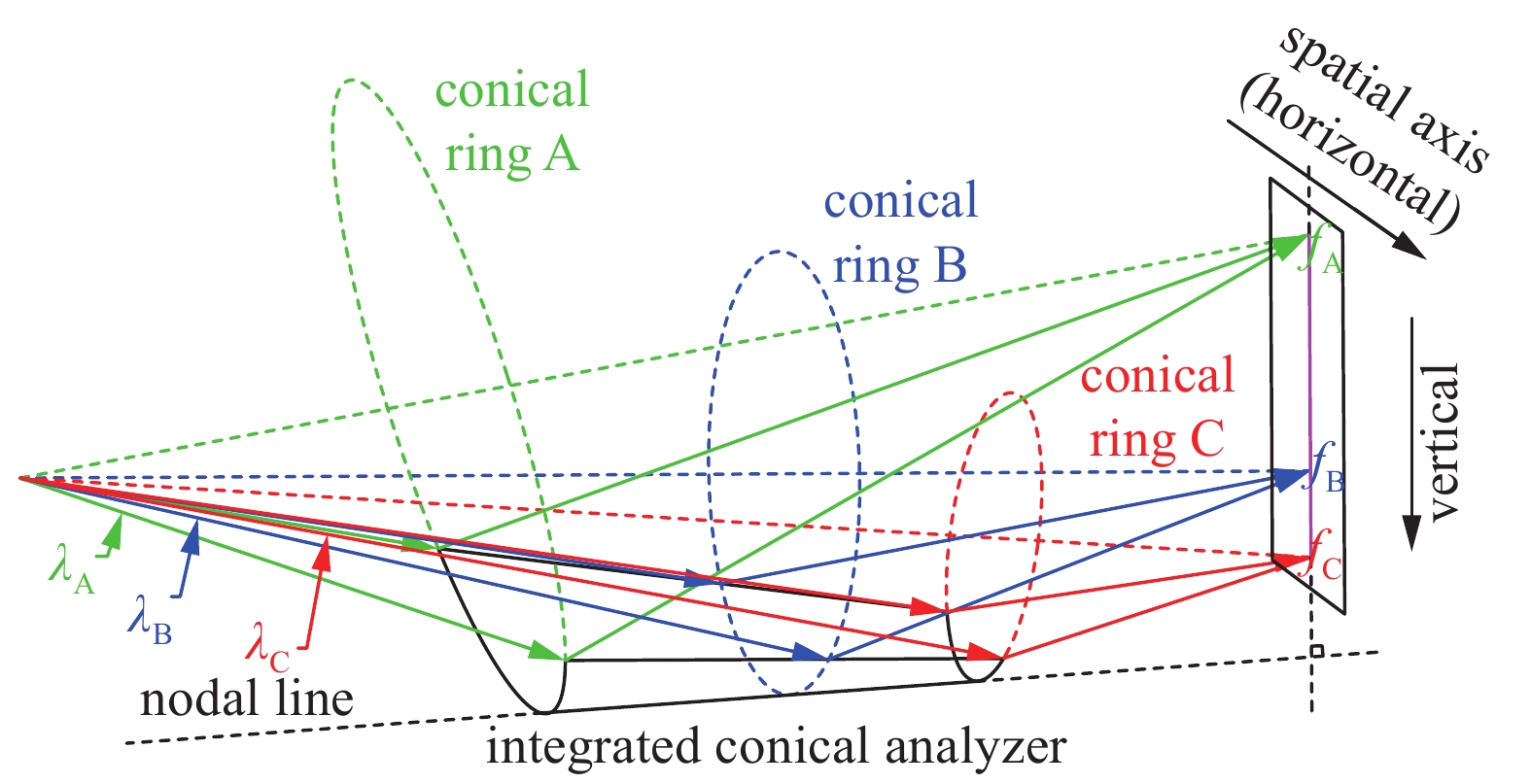[19] Morishita K, Hayashi K, Nakajima K. One-shot spectrometer for several elements using an integrated conical crystal analyzer[J]. Review of Scientific Instrument, 2012, 83: 013112. doi: 10.1063/1.3677326 [20] Bitter M, Hill K W, Gao L, et al. A multi-cone X-ray imaging Bragg crystal spectrometer[J]. Review of Scientific Instrument, 2016, 87: 11E333. doi: 10.1063/1.4960537 [21] Del Río M S, Dejus R J. XOP v2. 4: Recent developments of the X-ray optics software toolkit[C]//Proc of SPIE. 2011: 814115. -
下载:
点击查看大图
图(12)
计量
- 文章访问数: 2163
- HTML全文浏览量: 409
- PDF下载量: 116
- 被引次数: 0
