Recent research progress of optical Thomson scattering in laser-driven inertial confinement fusion
-
摘要: 当前，激光惯性约束聚变在越来越接近点火的极端能量密度条件下，实验与模拟的偏离逐渐增大，一个关键原因是缺乏对黑腔等离子体状态及其影响黑腔能量学和内爆对称性的细致研究和判断。光学汤姆逊散射主动式、诊断精确、参数完备的优点，使之成为激光惯性约束聚变黑腔等离子体状态参数精密诊断的标准方法。中国面向激光惯性约束聚变研究的光学汤姆逊散射实验技术的发展与神光系列激光装置的建设和在其上开展的物理实验紧密相关。近年来，四倍频汤姆逊散射实验技术在神光III原型和100 kJ激光装置上相继建立，部分实验结果不仅加深了对激光惯性约束聚变靶物理的认识，还反映了实验条件对汤姆逊散射诊断的影响，促进了实验技术的精密化发展。在未来，还需要进一步发展多支路汤姆逊散射、五倍频汤姆逊散射和超热相干汤姆逊散射等新技术，面向点火黑腔条件，大幅提升激光等离子体状态参数的诊断精度，开展新物理机制的探索和研究，在激光惯性约束聚变和其他高能量密度物理科学领域发挥更重要的作用。
-
关键词:
- 激光惯性约束聚变 /
- 光学汤姆逊散射 /
- 等离子体状态参数 /
- 激光等离子体不稳定性
Abstract: Currently, laboratory created energy density of laser-driven inertial confinement fusion (ICF) is extremely close to that for ignition, while the divergence between experiment and simulation is increasing. One of the key issues is the lack of advanced knowledge of laser-hohlraum coupling process, which has shown the complexity of hohlraum environment. Optical Thomson scattering (OTS) becomes the standard technique for diagnosing the ICF hohlraum plasma parameters, due to its capability of providing unperturbed, local and precise measurement. The development of OTS in China is closely related with the Shenguang series laser facilities, on which most of the ICF experiments are carried out. In recent years, 4ω(263 nm) Thomson scattering technique has been set up on Shenguang-III prototype and 100 kJ-level laser facility, the corresponding results help the understanding of ICF physics. In the near future, several novel methods will be developed, for high-precision diagnostics of ICF ignition hohlraum plasmas and the research of new physical phenomena. -
图 1 光学汤姆逊散射的光谱形貌与等离子体状态参数密切相关
Figure 1. Optical Thomson scattering (OTS) spectral distribution is closely related with plasma parameters
图 2 神光III原型Au盘靶实验排布示意图
Figure 2. Schematic of the Au disk experimental setup on Shenguang-III prototype
图 3 神光III原型Au盘靶轴线上不同空间位置的时间分辨汤姆逊散射离子谱信号
Figure 3. Thomson scattering spectra of ions from the Au disk experiment carried out on Shenguang-III prototype
图 4 神光III原型Au盘靶典型光谱拟合结果
Figure 4. Typical fitting results of Thomson scattering spectra from the Au disk experiment carried out on Shenguang-III prototype
图 5 通过光谱拟合获得的Au盘靶轴线上不同空间位置等离子体电子温度和流速的演化信息
Figure 5. Typical fitting results of electron temperature and plasma velocity in different location on the axis of the Au disk
图 6 实验获得的Au盘靶轴线上等离子体电子温度和等离子体流速的空间分布
Figure 6. Typical spatial distribution of electron temperature and plasma velocity on the axis of the Au disk
图 7 神光III原型单环充气腔靶汤姆逊散射实验排布示意图
Figure 7. Schematic of the gas-filled hohlraum experimental setup on Shenguang-III prototype
图 8 神光III原型充气黑腔内部不同特征区域的汤姆逊散射光谱演化
Figure 8. Thomson scattering spectra measured from different regions of the gas-filled hohlraum on Shenguang-III prototype
图 9 100 kJ激光装置复杂充气黑腔实验排布示意图及激光波形和辐射温度曲线
Figure 9. Schematic of the complex hohlraum experimental setup on 100 kJ-level laser facility
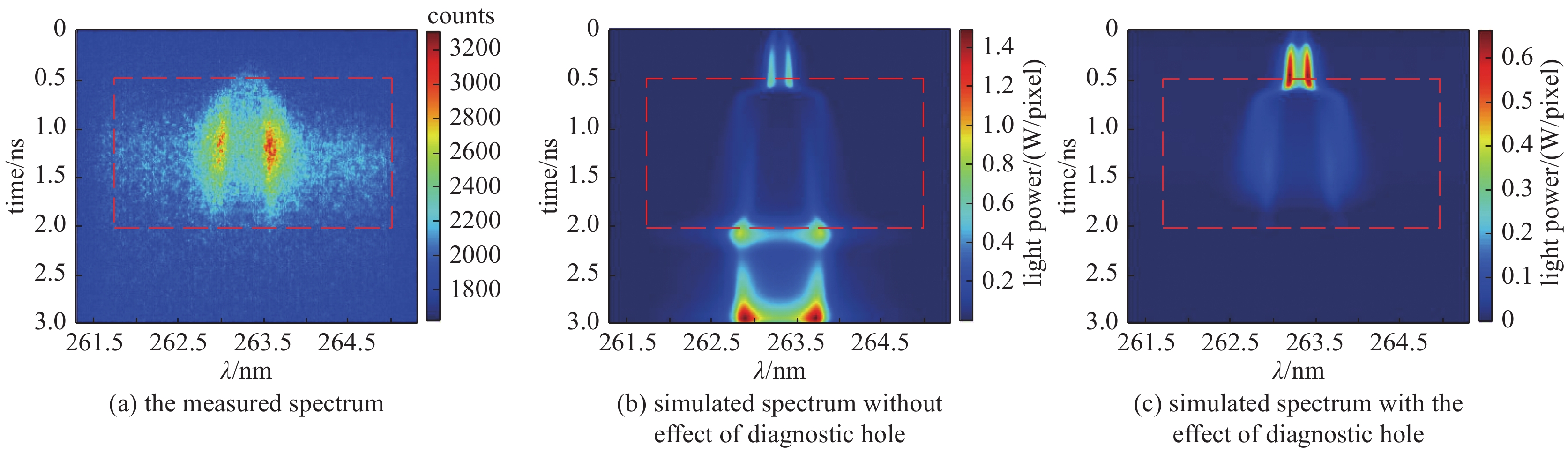
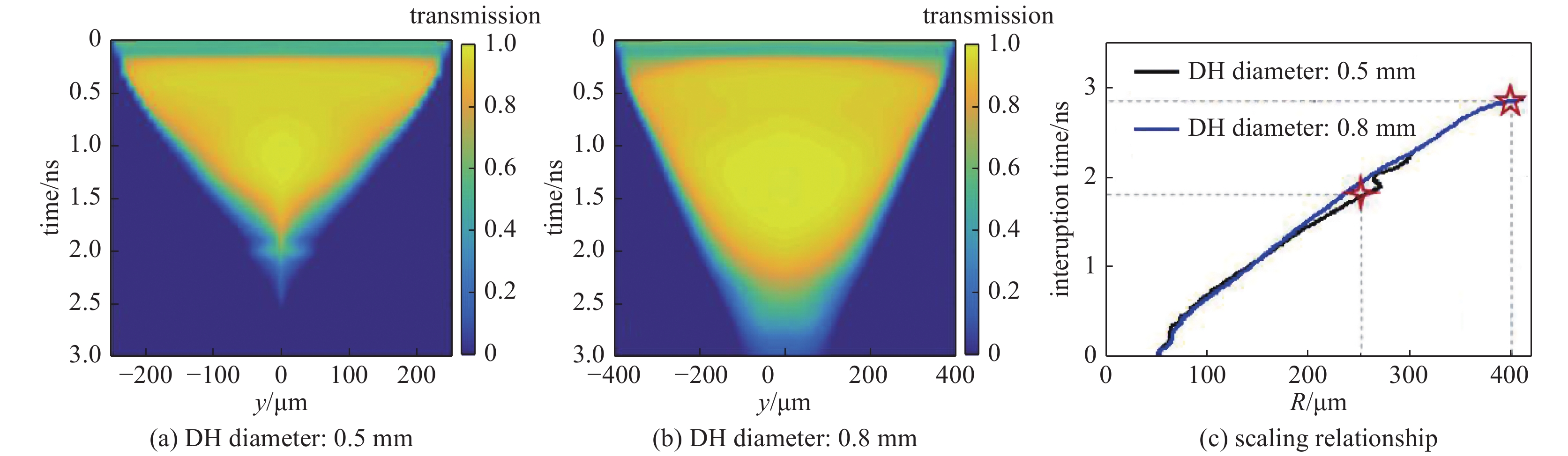
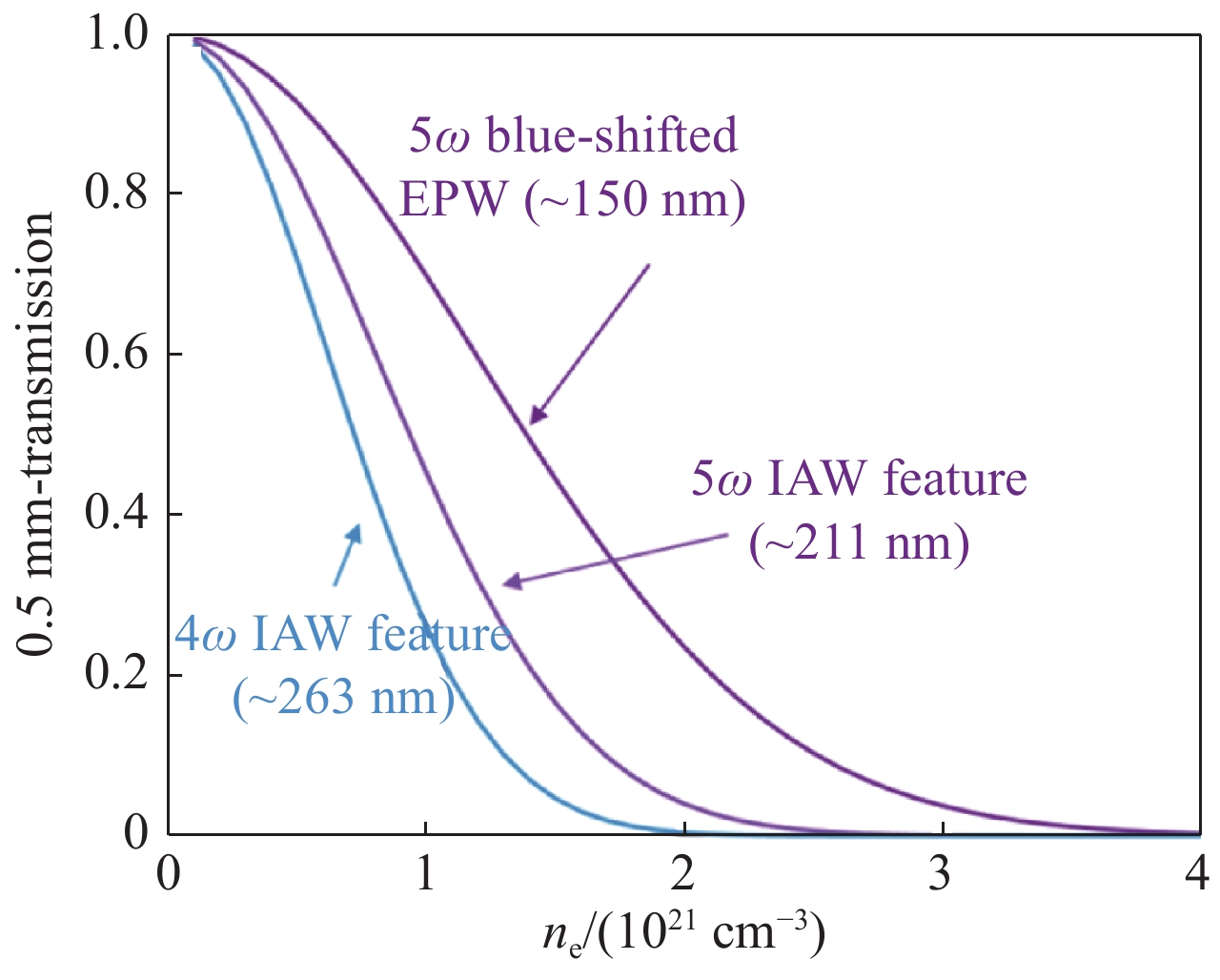
图 11 诊断孔直径为
$0.5\;{\text{m}}{\rm{m}}$ 和$0.8\;{\text{m}}{\rm{m}}$ 情况下的信号透过率行为模拟结果及散射光信号截止时刻与诊断孔半径的定标关系Figure 11. Simulation results of temporal behavior of the
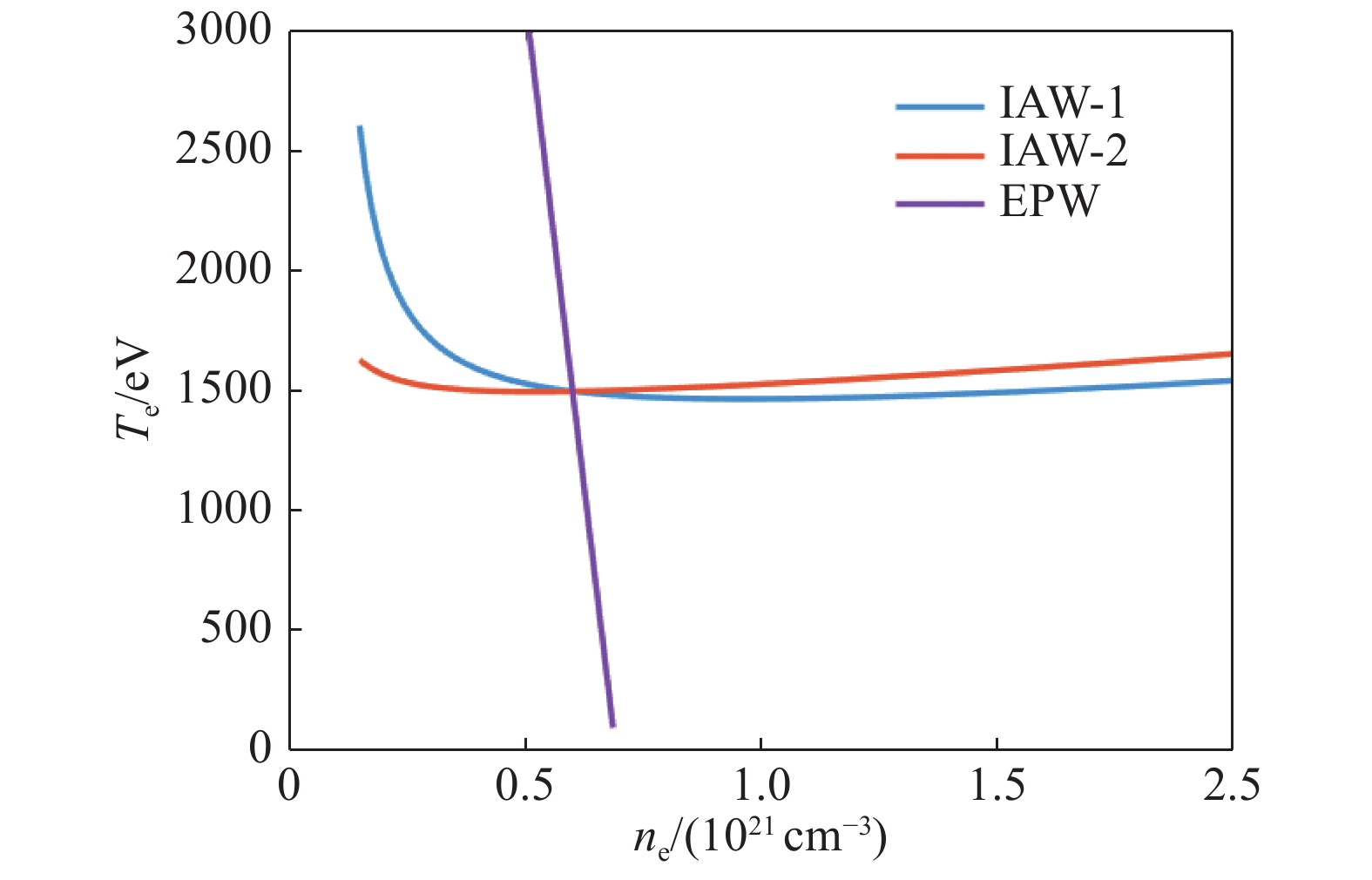
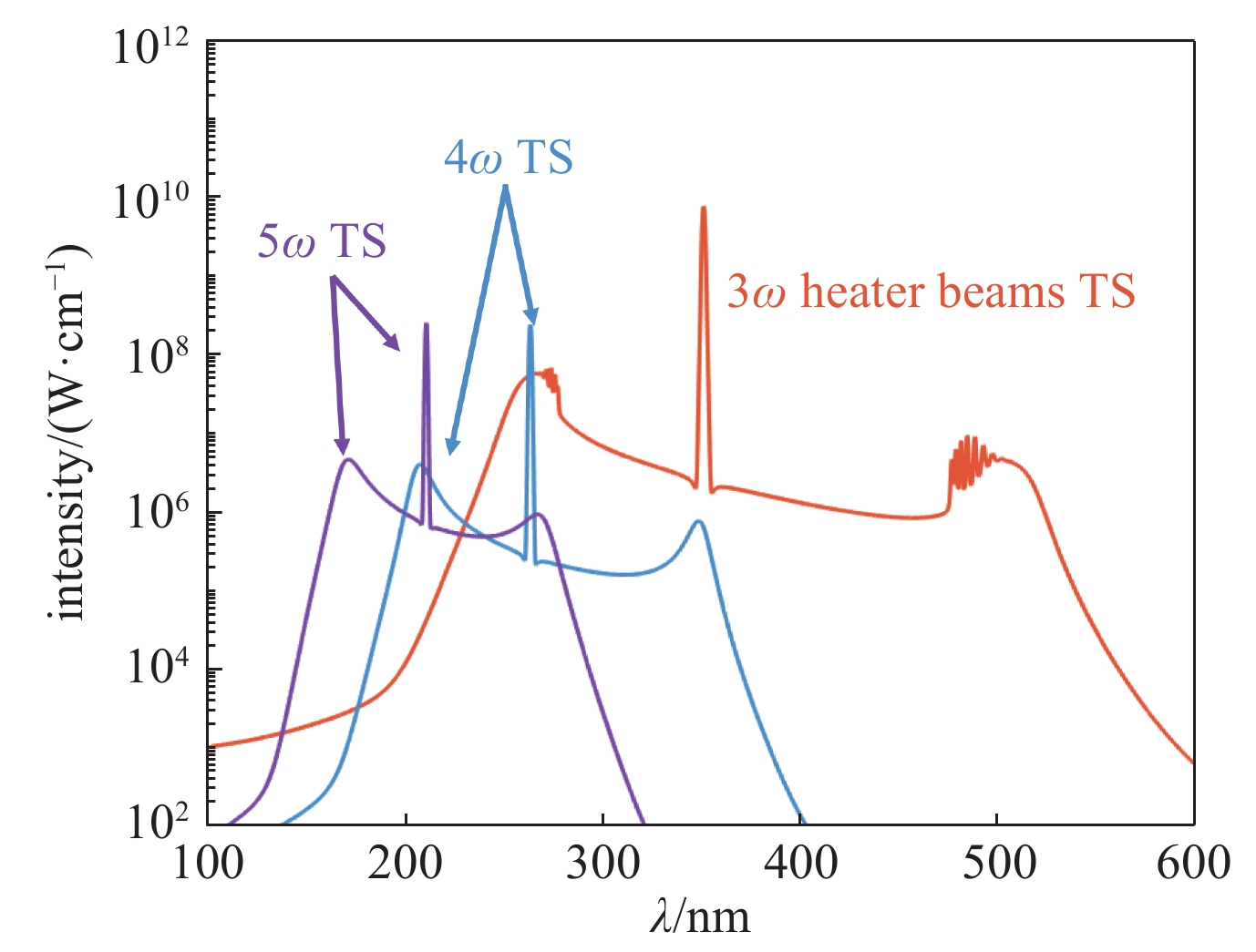
$4{\rm{\omega }}$ light transmission with spatial distribution along the DH radius and scaling relationship of the interruption time vs the diagnostic hole diameter
图 12 100 kJ激光装置上获得的充气六孔球腔全过程、高信噪比的汤姆逊散射光谱及两个特征时刻的光谱拟合结果
Figure 12. High-quality Thomson scattering spectrum of gas-filled octahedral spherical hohlraum on 100 kJ-level facility and fitting results at two typical time
图 13 单支路汤姆逊散射离子光谱参数拟合面临的难题：存在多解
Figure 13. Schematic of the fitting results by single Thomson scattering ion spectrum: Multiple plasma parameters can be obtained due to the uncertainty of electron density
图 14 多支路汤姆逊散射联合诊断示意图：利用不同信号对参数敏感度的差异化特点，能够大幅提升参数诊断精度和完备性
Figure 14. Schematic of simultaneous diagnosis of multiple Thomson scattering spectra: The precision of electron temperature and electron density will be increased
图 15 典型ICF黑腔条件下的汤姆逊散射光谱信号强度与加热束背景噪声的比对，五倍频汤姆逊散射信号有利于避开热束本身的汤姆逊散射产生的背景干扰
Figure 15. Comparison of Thomson scattering spectral distribution of
$5{\rm{\omega }}$ probe beam，$4{\rm{\omega }}$ probe beam，and$3{\rm{\omega }}$ heater beams.$5{\rm{\omega }}$ seems better to avoid the background noise produced by$3{\rm{\omega }}$ heater beams
图 16 不同波长信号光穿过等离子体的透过率比对，五倍频具有更显著的优势
Figure 16. Transmission comparison of Thomson scattering signal with different wave length.
$5{\rm{\omega }}$ seems better to propagate and detect higher electron density region
图 17 神光III原型装置超热相干汤姆逊散射实验排布、散射差矢与光谱结果
Figure 17. Schematic of experiment setup of superhot collective Thomson scattering on Shenguang-III prototype，k-vector diagram and experimental spectrum
-
[1] 李三伟, 杨冬, 李欣, 等. 我国激光间接驱动黑腔物理实验研究进展[J]. 中国科学: 物理学 力学 天文学, 2018, 48:065202. (Li Sanwei, Yang Dong, Li Xin, et al. Recent progress of hohlraum physics experiments in indirect driven ICF in China[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2018, 48: 065202 [2] Lindl J. Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain[J]. Physics of Plasmas, 1995, 2(11): 3933-4024. doi: 10.1063/1.871025 [3] Lindl J, Amendt P, Berger R L, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility[J]. Physics of Plasmas, 2004, 11(2): 339-491. doi: 10.1063/1.1578638 [4] Glenzer S H, Back C A, Suter L J, et al. Thomson scattering from inertial confinement fusion hohlraum plasmas[J]. Physical Review Letters, 1997, 79(7): 1277-1280. doi: 10.1103/PhysRevLett.79.1277 [5] Glenzer S, MacGowan B, Michel P, et al. Symmetric Inertial Confinement Fusion implosions at ultra-high laser energies[J]. Science, 2010, 327(5970): 1228-1231. doi: 10.1126/science.1185634 [6] National Nuclear Sccurity Administration. National Ignition campaign program completion report[R]. LLNL-TR-570412, 2021. [7] Lindl J, Landen O, Edward J, et al. Review of the National Ignition Campaign 2009-2012[J]. Physics of Plasmas, 2014, 21: 020501. [8] Guo Liang, Li Xin, Xie Xufei, et al. Experimental and simulation studies on gold bubble movement in gas-filled hohlraums[J]. Nuclear Fusion, 2019, 59: 016002. [9] 杨冬, 李志超, 李三伟, 等. 间接驱动惯性约束聚变中的激光等离子体不稳定性[J]. 中国科学: 物理学 力学 天文学, 2018, 48:065203. (Yang Dong, Li Zhichao, Li Sanwei, et al. Laser plasma instability in indirect-drive inertial confinement fusion[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2018, 48: 065203 [10] Froula D, Glenzer S, Luhmann N, et al. Plasma scattering of electromagnetic radiation: Theory and measurement techniques[J]. Fusion Science and Technology, 2012,61(1):104-105. [11] Bai Bo, Zheng Jian, Liu Wandong, et al. Thomson scattering measurement of gold plasmas produced with 0.351 μm laser light[J]. Physics of Plasmas, 2001, 8(9): 4144-4148. doi: 10.1063/1.1391445 [12] Bai Bo, Zheng Jian, Yu Changxuan, et al. Collective Thomson scattering from laser-produced plasmas[J]. Chinese Physics Letters, 2001, 18(7): 936-939. [13] 王哲斌. 激光聚变等离子体Thomson散射诊断[D]. 合肥: 中国科学技术大学, 2006: 121-286.Wang Zhebin. Thomson scattering of laser plasmas in relevance to inertial confinement fusion[D]. Hefei: University of Science and Technology of China, 2006: 121-286 [14] Wang Zhebin, Zheng Jian, Zhao Bin, et al. Thomson scattering from laser-produced gold plasmas in radiation conversion layer[J]. Physics of Plasmas, 2005, 12: 082703. [15] 李志超. 大尺度激光等离子体相互作用的实验研究[D]. 合肥: 中国科学技术大学, 2011: 11-199.Li Zhichao. Experimental research on large-scale laser-plasma interactions[D]. Hefei: University of Science and Technology of China, 2011: 11-199 [16] Li Zhichao, Zheng Jian, Jiang Xiaohua, et al. Methods of generation and detailed characterization of millimeter-scale plasmas using a gasbag target[J]. Chinese Physics Letters, 2011, 28: 125202. [17] Li Zhichao, Zheng Jian, Jiang Xiaohua, et al. Interaction of 0.53 μm laser pulse with millimeter-scale plasmas generated by gasbag target[J]. Physics of Plasmas, 2012, 19: 062703. [18] Gong Tao, Li Zhichao, Jiang Xiaohua, et al. Development of Thomson scattering system on Shenguang-III prototype laser facility[J]. Review of Scientific Instruments, 2015, 86: 023501. [19] 龚韬. 激光间接驱动惯性约束聚变中受激散射过程的理论和实验研究[D]. 合肥: 中国科学技术大学, 2015.Gong Tao. Theoretical and experimental study on the stimulated scattering in laser indirect-drive inertial confinement fusion [D]. Hefei: University of Science and Technology of China, 2015 [20] Zheng Wanguo, Wei Xiaofeng, Zhu Qihua, et al. laser performance upgrade for precise ICF experiment in SG-III laser facility[J]. Matter and Radiation at Extremes, 2017, 2(5): 243-250. doi: 10.1016/j.mre.2017.07.004 [21] Zhao Hang, Li Zhichao, Yang Dong, et al. Implementation of ultraviolet Thomson scattering on SG-III laser facility[J]. Review of Scientific Instruments, 2018, 89: 093505. [22] Zhao Hang, Li Zhichao, Yang Dong, et al. Progress in optical Thomson scattering diagnostics for ICF gas-filled hohlraums[J]. Matter and Radiation at Extremes, 2019, 4: 055201. doi: 10.1063/1.5090971 [23] Froula D H, Ross J S, Divol L, et al. Thomson scattering measurements of high electron temperature hohlraum plasmas for laser-plasma interaction studies[J]. Physics of Plasmas, 2006, 13: 052704. [24] Song Tianming, Yang Jiamin, Yang Dong, et al. Experimental study of the X-ray radiation source at approximately constant radiation temperature[J]. Plasma Science and Technology, 2013, 15(11): 1108-1111. doi: 10.1088/1009-0630/15/11/06 [25] Song Tianming, Yang Jiamin, Zhu Tuo, et al. Continued study of hohlraum radiation source at approximately constant radiation temperature[J]. Plasma Science and Technology, 2016, 18(4): 342-345. doi: 10.1088/1009-0630/18/4/02 [26] Li Zhichao, Jiang Xiaohua, Liu Shenye, et al. A novel flat-response X-ray detector in the photon energy range of 0.1–4 keV[J]. Review of Scientific Instruments, 2010, 81: 073504. [27] Li Zhichao, Zhu Xiaoli, Jiang Xiaohua, et al. Note: Continuing improvements on the novel flat-response X-ray detector[J]. Review of Scientific Instruments, 2011, 82: 106106. [28] 宋鹏, 翟传磊, 李双贵, 等. 激光间接驱动惯性约束聚变二维总体程序—LARED集成程序[J]. 强激光与粒子束, 2015, 27:032007. (Song Peng, Zhai Chuanlei, Li Shuanggui, et al. LARED–Integration code for numerical simulation of the whole process of the indirect-drive laser inertial confinement fusion[J]. High Power Laser and Particle Beams, 2015, 27: 032007 doi: 10.11884/HPLPB201527.032007 [29] Shan Lianqiang, Cai Hongbo, Zhang Huasen, et al. Experimental evidence of kinetic effects in indirect-drive inertial confinement fusion hohlraums[J]. Physical Review Letters, 2018, 120: 195001. [30] Jiang Shaoen, Wang Feng, Ding Yongkun, et al. Experimental progress of inertial confinement fusion based at the ShenGuang-III laser facility in China[J]. Nuclear Fusion, 2019, 59: 032006. [31] Huo Wenyi, Li Zhichao, Chen Yaohua, et al. First octahedral spherical hohlraum energetics experiment at the SGIII laser facility[J]. Physical Review Letters, 2018, 120: 165001. [32] Liu Yaoyuan, Ding Yongkun, Zheng Jian. Improvement in Thomson scattering diagnostic precision via fitting the multiple-wavenumber spectra simultaneously[J]. Review of Scientific Instruments, 2019, 90: 083501. [33] Ross J S. UV Thomson scattering on the NIF[C]//National ICF Diagnostic Working Group Meeting. 2015. [34] Gong Tao, Hao Liang, Li Zhichao, et al. Recent research progress of laser plasma interactions in Shenguang laser facilities[J]. Matter and Radiation at Extremes, 2019, 4: 055202. doi: 10.1063/1.5092446 [35] Kline J L, Montgomery D S, Bezzerides B, et al. Observation of a transition from fluid to kinetic nonlinearities for Langmuir waves driven by stimulated Raman backscatter[J]. Physical Review Letters, 2005, 94: 175003. [36] Rousseaux C, Gremillet L, Casanova M, et al. Transient development of backward stimulated Raman and Brillouin scattering on a picosecond time scale measured by subpicosecond Thomson diagnostic[J]. Physical Review Letters, 2006, 97: 015001. [37] Turnbull D, Michel P, Ralph J E, et al. Multibeam seeded Brillouin sidescatter in inertial confinement fusion experiments[J]. Physical Review Letters, 2015, 114: 125001. [38] Michel P, Divol L, Dewald E L, et al. Multibeam stimulated Raman scattering in inertial confinement fusion conditions[J]. Physical Review Letters, 2015, 115: 055003. [39] Neuville C, Tassin V, Pesme D, et al. Experimental evidence of the collective Brillouin scattering of multiple laser beams sharing acoustic waves[J]. Physical Review Letters, 2016, 116: 235002. doi: 10.1103/PhysRevLett.116.235002 -
下载:
点击查看大图
计量
- 文章访问数: 2358
- HTML全文浏览量: 518
- PDF下载量: 255
- 被引次数: 0
