Characteristic and impact of kinetic effects at interfaces of inertial confinement fusion hohlraums
-
摘要: 在惯性约束聚变物理研究中，等离子体界面处的动理学效应及其时空演化特性近年来受到重点关注，因为它会显著影响激光能量沉积、激光等离子体不稳定性、辐照对称性、黑腔和内爆性能等诸多物理。准确描绘等离子体特征界面附近的动理学效应是惯性约束聚变物理设计的基本需求，也是高能量密度物理中的具有挑战且未完全解决的问题。重点回顾近几年来本团队围绕等离子体动理学效应及其影响开展的一些研究工作：（1）聚变黑腔中金等离子体与靶丸冕区等离子体边缘处的电场结构及其加速的高能离子对内爆对称性的影响；（2）激光光路上高Z-低Z等离子体界面处的电场产生机制及其导致的反常离子扩散对激光等离子体不稳定性的影响；（3）等离子体中电磁场结构的质子照相反演。Abstract: In the study of inertial confinement fusion physics, the characteristics, temporal and spatial evolution of kinetic effects at the plasma interfaces attract crucial interest recently because they can affect the laser energy deposition, laser plasma instabilities, radiation asymmetry and implosion performance. A successful design of inertial confinement fusion requires the accurate description of the temporal and spatial evolution of the kinetic effects at the plasma interfaces, which is also a very challenging and unresolved problem in high energy density physics. In this paper, we will review our recent researches on the kinetic effects and their influence on laser plasma instabilities and implosion performance: (1) Electrostatic field arisen in the hohlraum wall/ablator (or the low-density fill-gas) interpenetration region will result in efficient acceleration of high energy ions, which is a source of the low-mode asymmetry of the implosion capsule. (2) The mechanism for the electrostatic field generation and the anomalous mix in the interpenetration layer at the high-Z and low-Z plasma interface and its effects on the laser plasma instabilities. (3) Reconstruction of the spontaneous electric and magnetic fields through proton radiography.
-
图 1 （a）神光III原型装置间接驱动近真空黑腔示意图，（b）动理学效应验证实验靶丸设计优化
Figure 1. （a） Schematic diagram of indirect-drive near-vacuum hohlraum target at Shengguang-III prototype laser facility，（b） optimization of the target design for the experimental demonstration of kinetic effects
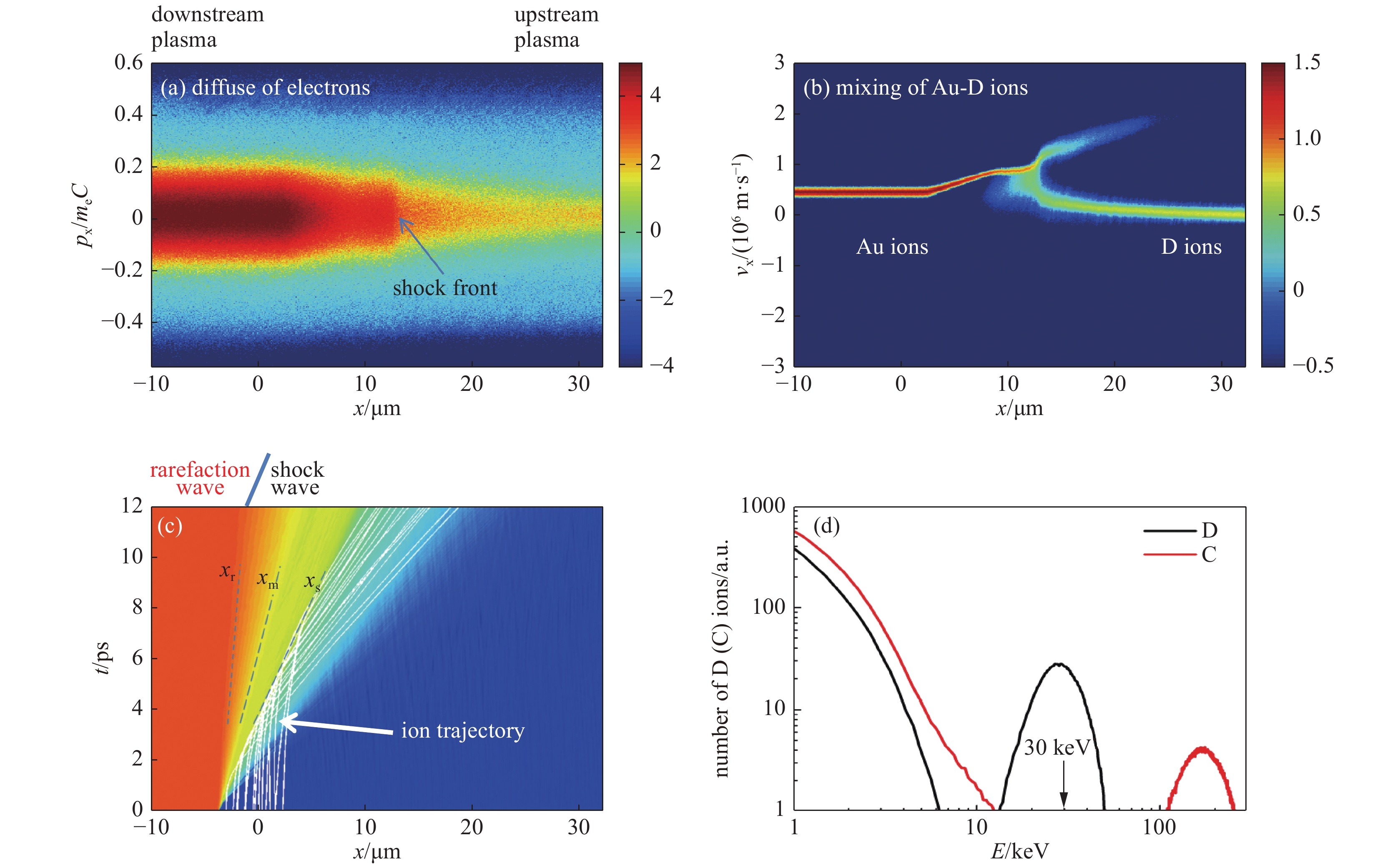
图 2 PIC模拟得到的（a）电子和（b）离子相空间分布图；（c）平均离子密度（y方向平均）随时间变化图；（d）5 ns时刻冲击波前沿CD 离子能谱分布. 引自文献[18]
Figure 2. （a）Phase space of vx～x for（a）electrons and（b）ions；（c）The evolution of the plasma density averaged over the y-direction；（d）Energy spectra of the CD ions within the precursor region at t＝5 ps. This figure is reproduced from Ref [18]
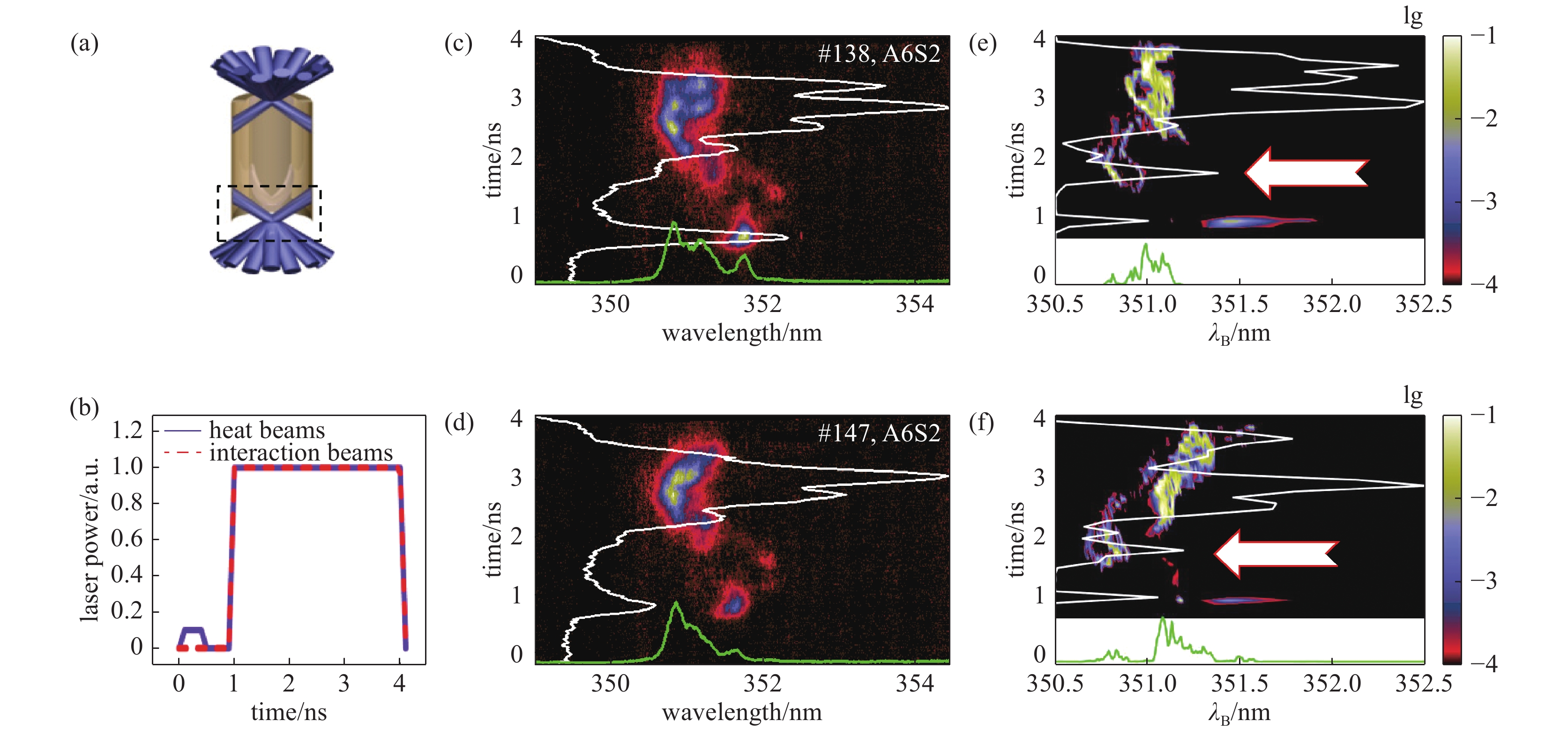
图 3 （a）激光排布和（b）激光脉冲示意图，（c）138发和（d）147发测量的光谱，（e）138发和（f）147发的模拟光谱，引自文献[27]（将（b）图改为激光脉冲）
Figure 3. Sketch of （a） laser arrangement and （b） laser pulse. Streaked spectra of SBS for （c） the shot 138 and （d） the shot 147. Simulated spectra of SBS for （e） the shot 138 and （f） the shot 147. The figures are cited from Ref[27]
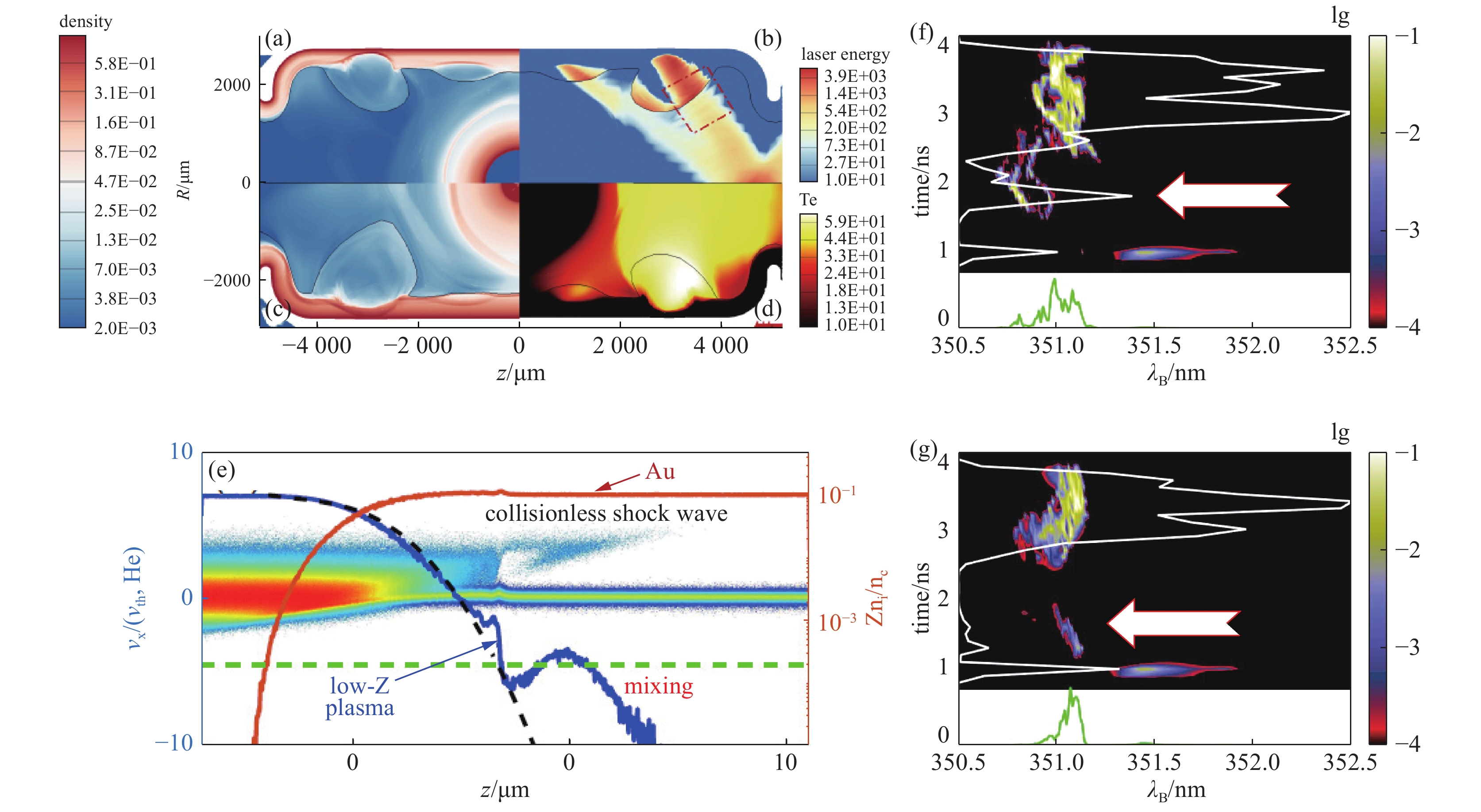
图 4 （a-d）典型ICF柱腔（Au）的辐射流体模拟流场分布图,（e）氦和金离子的相空间图,（f）不考虑和（g）考虑离子混合的SBS模拟光谱, 引自文献[27]和[28]
Figure 4. （a-d） Radiation hydrodynamic simulations by LARED-integration for a typical cylindrical Au hohlraum for ICF. （e） Phase space of He ions and Au ions. Simulated spectra of SBS （f） without and （g） with considering ion mix. The figure are cited from Ref. [27] and [28]
图 5 Weibel不稳定性（a）自生磁场
${B_y}$ 和（b）自生电场${E_x}$ 在t＝1.06 ps时的空间分布特征Figure 5. Spatial distribution of the self-generated（a）magnetic field
${B_y}$ and（b）electric field Ex of the Weibel instability at t＝1.06 ps
-
[1] Edwards M J, Patel P K, Lindl J D, et al. Progress towards ignition on the National Ignition Facility[J]. Physics of Plasmas, 2013, 20: 070501. doi: 10.1063/1.4816115 [2] Hurricane O A, Callahan D A, Springer P T, et al. Beyond alpha-heating: driving inertially confined fusion implosions toward a burning-plasma state on the National Ignition Facility[J]. Plasma Physics Controlled Fusion, 2019, 61: 014033. [3] Kritcher A L, Hinkel D E, Callahan D A, et al. Integrated modeling of cryogenic layered highfoot experiments at the NIF[J]. Physics of Plasmas, 2016, 23(5): 052709. doi: 10.1063/1.4949351 [4] Hopkins L F Berzak, Pape S Le, Divol L, et al. Near-vacuum hohlraums for driving fusion implosions with high density carbon ablators[J]. Physics of Plasmas, 2015, 22: 056318. doi: 10.1063/1.4921151 [5] Rinderknecht H G, Amendt P A, Wilks S C, et al. Kinetic physics in ICF: present understanding and future directions[J]. Plasma Physics Controlled Fusion, 2018, 60: 064001. [6] Ross J S, Park H S, Amendt P, et al. Thomson scattering diagnostic for the measurement of ion species fraction[J]. Review of Scientific Instruments, 2012, 83: 10E323. doi: 10.1063/1.4731007 [7] Bellei C, Amendt P A, Wilks S C, et al. Species separation in inertial confinement fusion fuels[J]. Physics of Plasmas, 2013, 20: 012701. doi: 10.1063/1.4773291 [8] Kirkwood R K, Moody J D, Kline J, et al. A review of laser–plasma interaction physics of indirect-drive fusion[J]. Plasma Physics Controlled Fusion, 2013, 55: 103001. [9] Shan L Q, Cai H B, Zhang W S, et al. Experimental evidence of kinetic effects in indirect-drive inertial confinement fusion hohlraums[J]. Physical Review Letters, 2018, 120: 195001. doi: 10.1103/PhysRevLett.120.195001 [10] Cai H B, Shan L Q, Yuan Z Q, et al. Study of the kinetic effects in indirect-drive inertial confinement fusion hohlraums[J]. High Energy Density Physics, 2020, 36: 100756. doi: 10.1016/j.hedp.2020.100756 [11] Li C K, Seguin F H, Frenje J A, et al. Diagnosing indirect-drive inertial-confinement-fusion implosions with charged particles[J]. Plasma Physics and Controlled Fusion, 2010, 52: 124027. [12] Turnbull D, Colaitis A, Hansen A M, et al. , Impact of the Langdon effect on crossed-beam energy transfer[J]. Nature Physics, 2019, 16: 181-185. [13] 蔡洪波, 周沧涛, 贾青, 等. 激光驱动强流电子束产生和控制[J]. 强激光与粒子束, 2015, 27:032001. (Cai Hongbo, Zhou Cangtao, Jia Qing, et al. Laser-driven relativistic electron beam for fast ignition[J]. High Power Laser and Particle Beams, 2015, 27: 032001 doi: 10.11884/HPLPB201527.032001 [14] Thoma C, Welch D R, Clark R E, et al. Hybrid-PIC modeling of laser-plasma interactions and hot electron generation in gold hohlraum walls[J]. Physics of Plasmas, 2017, 24: 062707. doi: 10.1063/1.4985314 [15] Molvig K, Vold E L, Dodd E S, et al. Nonlinear structure of the diffusing gas-metal interface in a thermonuclear plasma[J]. Physical Review Letters, 2012, 109: 095001. [16] Braginskii S I. Transport process in a plasma[J]. Reviews of Plasma Physics, 1965, 1: 205-311. [17] Li C K, Petrasso R D. Charaged-particle stopping powers in inertial confinement fusion plasmas[J]. Physical Review Letters, 1993, 70(20): 3059-3063. doi: 10.1103/PhysRevLett.70.3059 [18] Zhang W S, Cai H B, Shan L Q, et al. Anomalous neutron yield in indirect-drive inertial-confinement-fusion due to the formation of collisionless shocks in the corona[J]. Nuclear Fusion, 2017, 57(17): 066012. [19] Kirkwood R K, Moody J D, Kline J, et al. A review of laser–plasma interaction physics of indirect-drive fusion[J]. Plasma Physics and Controlled Fusion, 2013, 55: 103001. [20] Kirkwood R K, Michel P, London R. et al. Multi-beam effects on backscatter and its saturation in experiments with conditions relevant to ignition[J]. Physics of Plasmas, 2011, 18: 056311. doi: 10.1063/1.3587122 [21] Turnbull D, Michel P, Ralph J E, et al. Multibeam seeded Brillouin sidescatter in inertial confinement fusion experiments[J]. Physical Review Letters, 2015, 114(12): 125001. doi: 10.1103/PhysRevLett.114.125001 [22] Myatt J F, Zhang J, Short R W, et al. Multiple-beam laser–plasma interactions in inertial confinement fusion[J]. Physics of Plasmas, 2014, 21: 055501. doi: 10.1063/1.4878623 [23] Dewald E L, Hartemann F, Michel P, et al. Generation and beaming of early hot electrons onto the capsule in laser-driven ignition hohlraums[J]. Physics Review Letters, 2016, 116: 075003. doi: 10.1103/PhysRevLett.116.075003 [24] Kruer W L, Wilks S C, Afeyan B B, et al. Energy transfer between crossing laser beams[J]. Physics of Plasmas, 1996, 3(1): 382-385. doi: 10.1063/1.871863 [25] Hall G N, Jones O S, Strozzi D J, et al. The relationship between gas fill density and hohlraum drive performance at the National Ignition Facility[J]. Physics of Plasmas, 2017, 24: 052706. doi: 10.1063/1.4983142 [26] 杨冬, 李志超, 李三伟, 等. 间接驱动惯性约束聚变中的激光等离子体不稳定性[J]. 中国科学: 物理学 力学 天文学, 2018, 48:065203. (Yang Dong, Li Zhichao, Li Sanwei, et al. Laser plasma instability in indirect-drive inertial confinement fusion[J]. Scientia Sinica-Physica Mechanica&Astronamica, 2018, 48: 065203 doi: 10.1360/SSPMA2018-00056 [27] Gong T, Hao L, Li Z, et al. Recent research progress of laser plasma interactions in Shenguang laser facilities[J]. Matter and Radiation at Extremes, 2019, 4: 055202. doi: 10.1063/1.5092446 [28] Hao L, Yang D, Li X, et al. Investigation on laser plasma instability of the outer ring beams on SGIII laser facility[J]. AIP Advances, 2019, 9: 095201. doi: 10.1063/1.5087936 [29] Yan X X, Cai H B, Zhang W S, et al. Anomalous mix induced by a collisionless shock wave in an inertial confinement fusion hohlraum[J]. Nuclear Fusion, 2019, 59: 106016. [30] Froula D H, Ross J S, Pollock B B, et al. Quenching of the nonlocal electron heat transport by large external magnetic fields in a laser-produced plasma measured with imaging Thomson scattering[J]. Physical Review Letters, 2007, 98: 135001. doi: 10.1103/PhysRevLett.98.135001 [31] 张恩浩, 蔡洪波, 杜报, 等. 激光聚变黑腔中等离子体的热流研究[J]. 物理学报, 2020, 69:035204. (Zhang Enhao, Cai Hongbo, Du Bao, et al. Heat flow of laser-ablated gold plasma in inertial confinement fusion hohlraum[J]. Acta Phys Sin, 2020, 69: 035204 doi: 10.7498/aps.69.20191423 [32] Fiuza F, Fonseca R A, Tonge J, et al. Weibel-instability-mediated collisionless shocks in the laboratory with ultraintense lasers[J]. Physical Review Letters, 2012, 108: 235004. doi: 10.1103/PhysRevLett.108.235004 [33] Manuel M J E, Li C K, Séguin F H, et al. First measurements of Rayleigh-Taylor-induced magnetic fields in laser-produced plasmas [J]. Physical Review Letters, 108 : 255006. [34] 项志遴, 俞昌旋. 高温等离子体诊断技术 [M]. 上海:上海科学技术出版社, 1982.Xiang Zhilin, Yu Changxuan. High temperature plasma diagnotics [M]. Shanghai: Shanghai Scientific&Technical Publishing, 1982 [35] Kaluza M C, Schlenvoigt H P, Mangles S, et al. Measurement of magnetic-field structures in a laser-wakefield accelerator[J]. Physical Review Letters, 2010, 105: 115002. doi: 10.1103/PhysRevLett.105.115002 [36] Li C K, Séguin F H, Rygg J R, et al. Measuring E and B fields in laser-produced plasmas with monoenergetic proton radiography[J]. Physical Review Letters, 2006, 97: 135003. doi: 10.1103/PhysRevLett.97.135003 [37] Rygg J R, Séguin F H, Li C K, et al. Proton radiography of inertial fusion implosions[J]. Science, 2008, 319: 1223-1225. doi: 10.1126/science.1152640 [38] Wang W W, Cai H B, Teng J, et al. Efficient production of strong magnetic fields from ultraintense ultrashort laser pulse with capacitor-coil target[J]. Physics of Plasmas, 2018, 25: 083111. doi: 10.1063/1.5000991 [39] Zhang H, Shen B F, Wang W P, et al. Collisionless shock acceleration of high-flux quasimonoenergetic proton beams driven by circularly polarized laser pulses[J]. Physical Review Letters, 2017, 119: 164801. doi: 10.1103/PhysRevLett.119.164801 [40] Higginson A, Gray R J, King M, et al. Near-100 MeV protons via a laser-driven transparency-enhanced hybrid acceleration scheme[J]. Nature Communication, 2018, 9: 724. doi: 10.1038/s41467-018-03063-9 [41] Huntington C M, Fiuza F, Ross J S, et al. Observation of magnetic field generation via the Weibel instability in interpenetrating plasma flows[J]. Nature Physics, 2015, 11: 173-176. doi: 10.1038/nphys3178 [42] Weibel E S. Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution[J]. Physical Review Letters, 1959, 2(3): 83-84. doi: 10.1103/PhysRevLett.2.83 [43] Fox W, Fiksel G, Bhattacharjee A, et al. Filamentation instability of counterstreaming laser-driven plasmas[J]. Physical Review Letters, 2013, 111: 225002. doi: 10.1103/PhysRevLett.111.225002 [44] Jia Q, Cai H B, Wang W W, et al. Effects of the background plasma temperature on the current filamentation instability[J]. Physics of Plasmas, 2013, 20: 032113. doi: 10.1063/1.4796052 [45] 贾青. 束流-等离子体系统中韦伯不稳定性的解析分析及模拟应用[D]. 北京: 北京大学, 2015.Jia Qing. Analytical analysis and simulated applications of Weibel in stability in beam-plasma system [D]. Beijing: Peking University, 2015 [46] Cai H B, Zhu S P, He X T, et al. Magnetic collimation of fast electrons in specially engineered targets irradiated by ultraintense laser pulses[J]. Physics of Plasmas, 2011, 18: 023106. doi: 10.1063/1.3553453 [47] Cai H B, Mima K, Zhou W M, et al. Enhancing the number of high-energy electrons deposited to a compressed pellet via double cones in fast ignition[J]. Physical Review Letters, 2009, 102: 245001. doi: 10.1103/PhysRevLett.102.245001 [48] Zhang F, Cai H B, Zhou W M, et al. Enhanced energy coupling for indirect-drive fast-ignition fusion targets[J]. Nature Physics, 2020, 16(7): 810-814. doi: 10.1038/s41567-020-0878-9 [49] Quinn K, Romagnani L, Ramakrishna B, et al. Weibel-induced filamentation during an ultrafast laser-driven plasma expansion[J]. Physical Review Letters, 2012, 108: 135001. doi: 10.1103/PhysRevLett.108.135001 [50] Kugland N L, Ryutov D D, Chang P Y, et al. Self-organized electromagnetic field structures in laser-produced counter-streaming plasmas[J]. Nature Physics, 2012, 8: 809-812. doi: 10.1038/nphys2434 [51] Du B, Cai H B, Zhang W S, et al. A demonstration of extracting the strength and wavelength of the magnetic field generated by the Weibel instability from proton radiography[J]. High Power Laser Science and Engineering, 2019, 7: e40. doi: 10.1017/hpl.2019.30 [52] 杜报, 蔡洪波, 张文帅, 等. Weibel不稳定性自生电磁场对探针质子束的偏转作用研究[J]. 物理学报, 2019, 68:185205. (Du Bao, Cai Hongbo, Zhang Wenshuai, et al. Deflection effect of electromagnetic field generated by Weibel instability on proton probe[J]. Actaica Physica Sinica, 2019, 68: 185205 doi: 10.7498/aps.68.20190775 [53] Du B, Cai H B, Zhang W S, et al. Distinguishing and diagnosing the spontaneous electric and magnetic fields of Weibel instability through proton radiography[J]. Plasma Physics and Controlled Fusion, 2020, 62: 025017. [54] Dieckmann M E. The filamentation instability driven by warm electron beams: statistics and electric field generation[J]. Plasma Physics and Controlled Fusion, 2009, 51: 124042. -
下载:
点击查看大图
图(7)
计量
- 文章访问数: 2233
- HTML全文浏览量: 565
- PDF下载量: 196
- 被引次数: 0
