Simulation analysis of background field enhancement of four-rail electromagnetic launcher
-
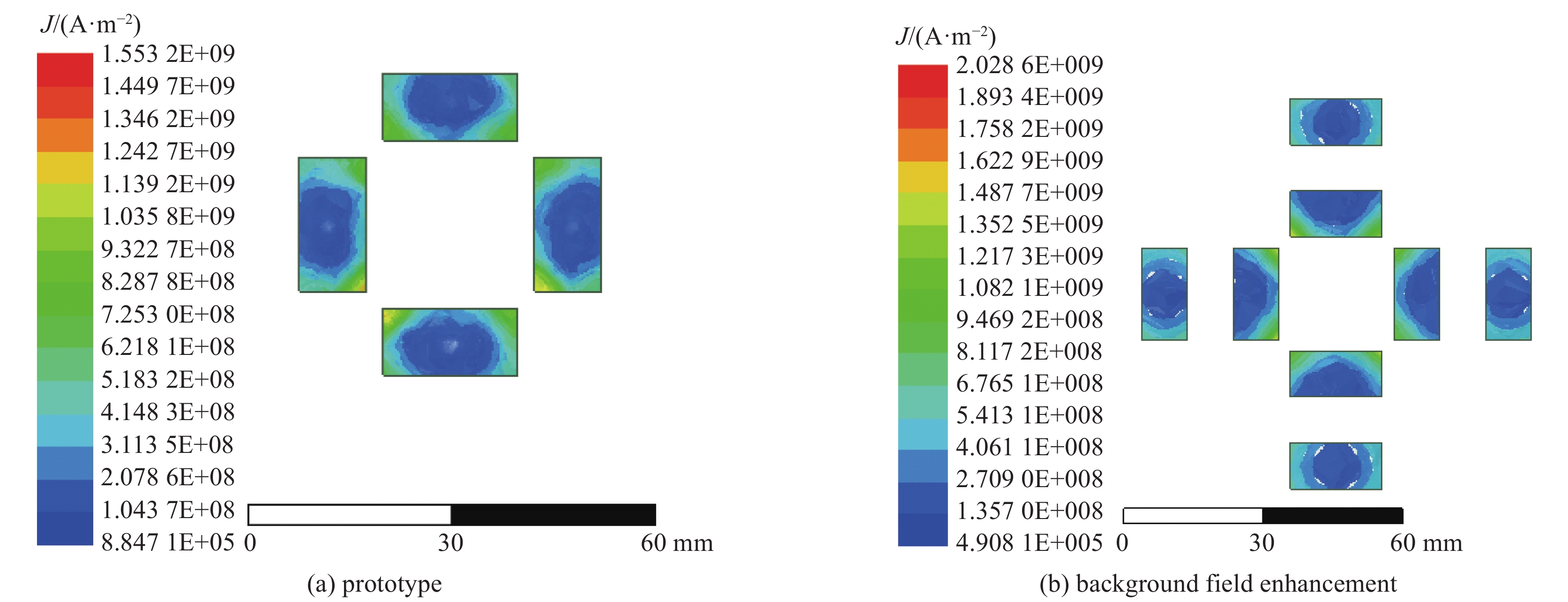
摘要: 针对四轨电磁发射器的背场增强方案的电感梯度进行了仿真分析。根据虚功原理,推导了背场下的四轨电磁发射器电感梯度公式。建立了三维背场仿真模型,分析了不同主、附轨道参数下电感梯度的变化规律。仿真结果表明:添加背场后,增大发射器口径、减小主附轨间距和附轨道截面积均能够实现系统电感梯度的提升;背场增强下,在主轨道高度达到口径的57%时,邻近效应已变得明显;相同附轨道截面积下,为增大系统电感梯度应优先减小附轨道厚度,为缓解电流邻近效应可优先减小附轨道高度;凹形截面附轨道能够明显改善电流邻近效应。Abstract: The inductance gradient of the background field enhancement scheme of the four-rail electromagnetic launcher is simulated. Based on the principle of virtual work, the formula of the inductance gradient of the four-rail launchers under the background field is derived. A three-dimensional background field simulation model is established to analyze the variation law of inductance gradient under different main and additional rail parameters. The simulation results show that the inductance gradient of the system can be improved by increasing the launcher caliber, reducing the distance between the main and additional rails and the cross-sectional area of the additional rails. With the enhancement of background field, the proximity effect becomes obvious when the height of main rail reaches 57% of the caliber. Under the same cross-sectional area, the thickness of the additional rails should be reduced to increase the inductance gradient of the system, and the height of the additional rails should be reduced to alleviate the proximity effect. Concave cross-section additional rail can obviously improve the current proximity effect.
-
表 1 不同主轨道间距下电感梯度
Table 1. Inductance gradients under different main rail spacing
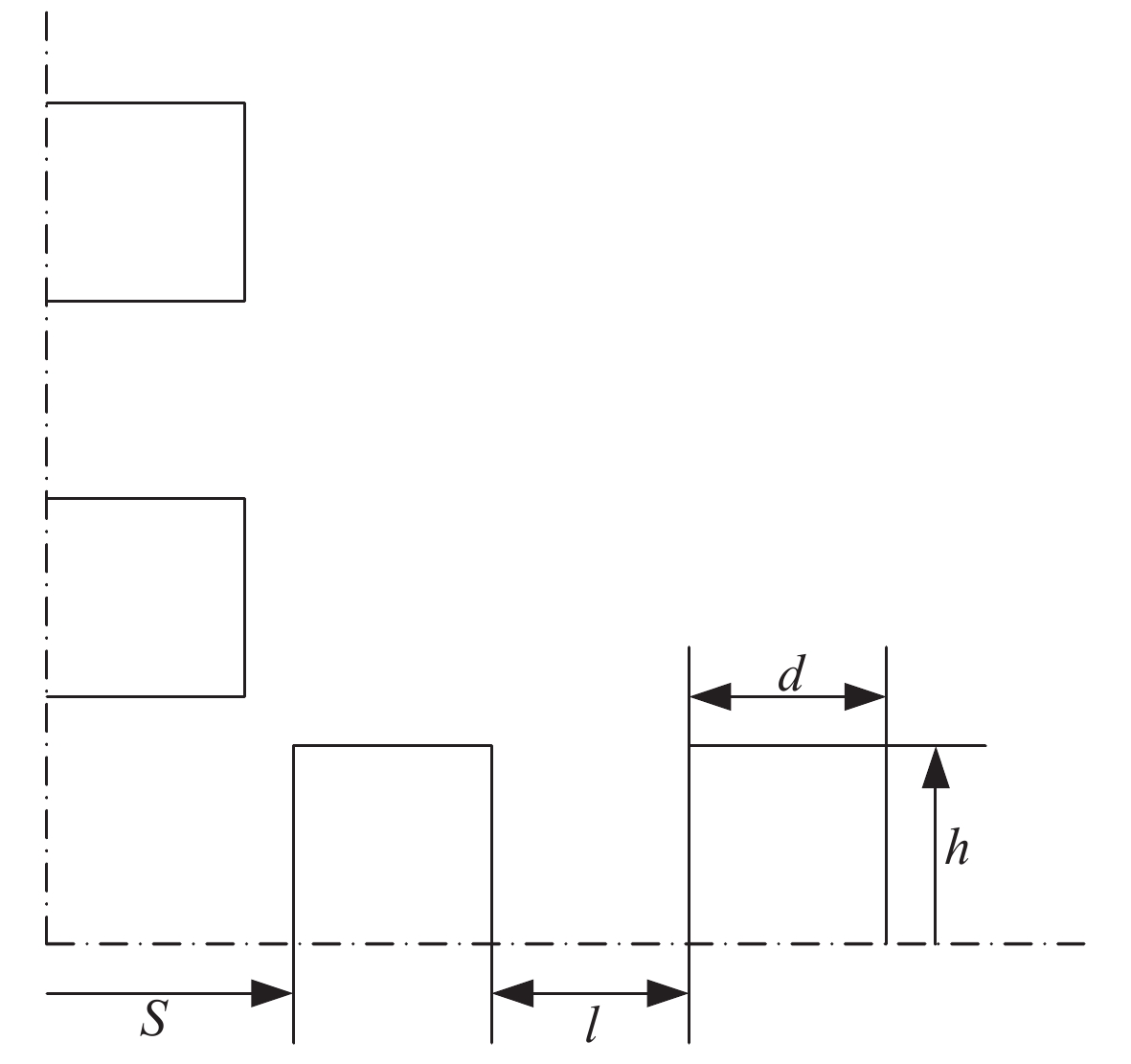
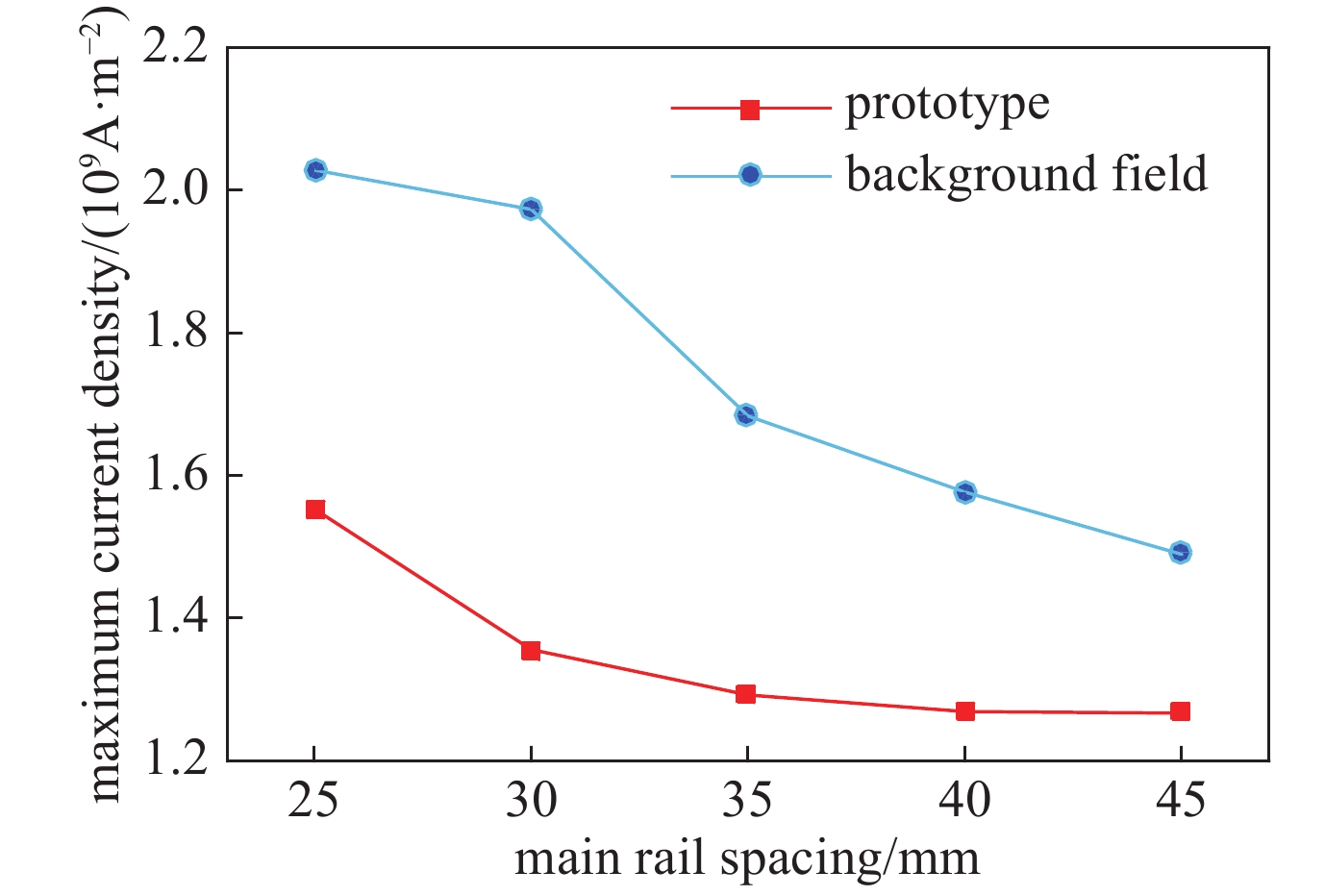
spacing/mm prototype/(µH·m−1) background field/(µH·m−1) Maxwell’s COMSOL’s Maxwell’s COMSOL’s 25 0.72363 0.74873 1.28442 1.3455 30 0.87762 0.85420 1.60369 1.5579 35 1.0041 0.94764 1.90189 1.75 40 1.114346 1.03030 2.14893 1.925 45 1.221838 1.10470 2.37343 2.0821 表 2 不同主附轨道间距下电感梯度
Table 2. Inductance gradients under different main and additional rail spacing
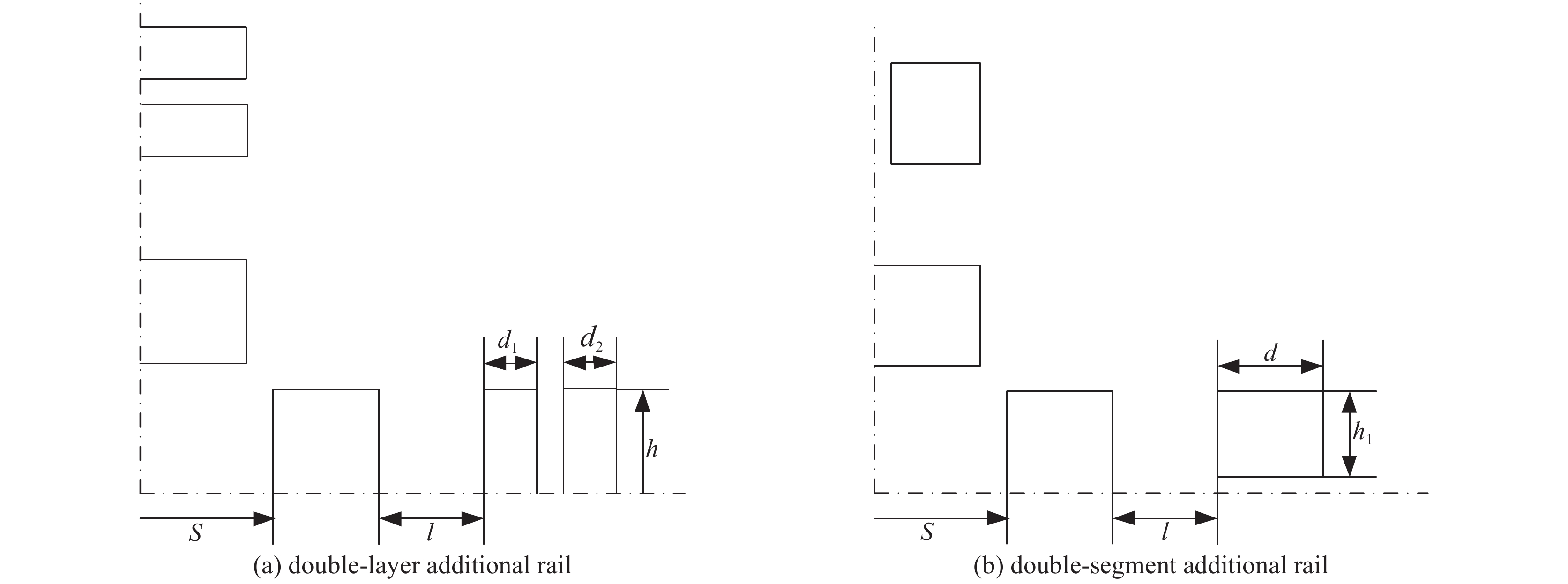
main and additional rail spacing/mm Maxwell’s solution/(µH·m−1) COMSOL’s solution/(µH·m−1) 2 1.5746 1.6911 4 1.47618 1.5831 6 1.39424 1.4913 8 1.32861 1.413 10 1.28442 1.3455 表 3 不同附轨道厚度下电感梯度
Table 3. Inductance gradients under different additional rail thicknesses
additional rail
thickness/mmMaxwell’s solution/
(µH·m−1)COMSOL’s solution/
(µH·m−1)Maximum current density/
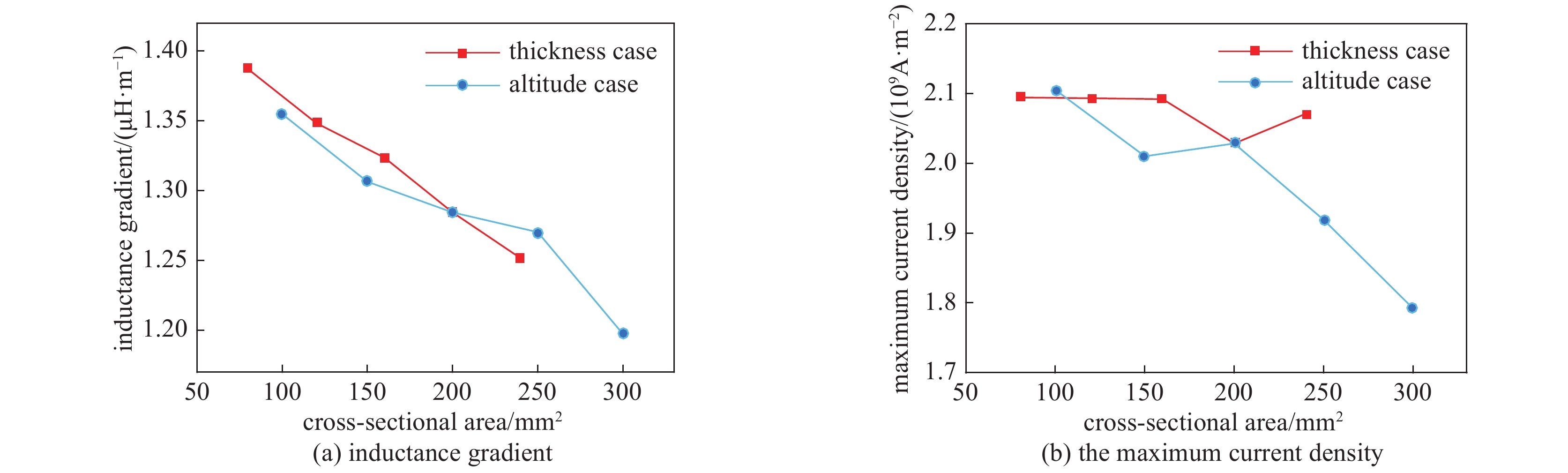
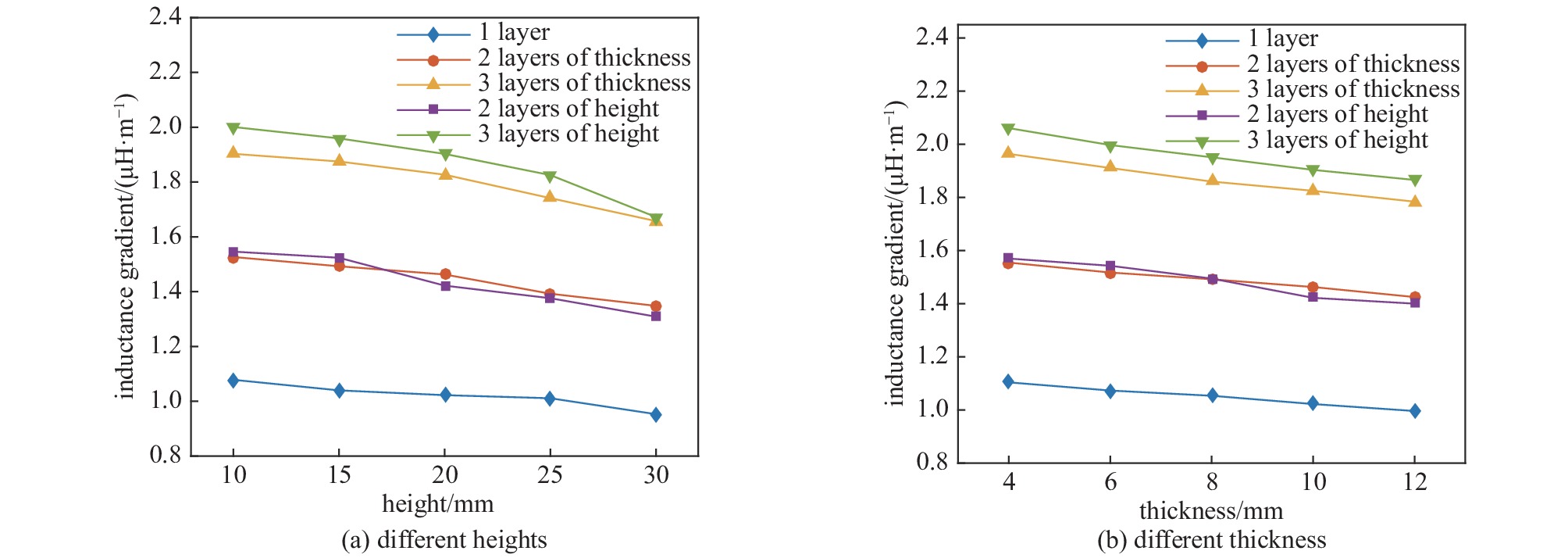
(109A·m−2)4 1.38708 1.4409 2.0946 6 1.34843 1.406 2.0935 8 1.32368 1.3746 2.0922 10 1.28442 1.3455 2.0286 12 1.25154 1.3199 2.0713 表 4 不同附轨道高度下电感梯度
Table 4. Inductance gradients at different additional rail heights
additional rail
altitude/(mm)Maxwell’s solution/
(µH·m−1)COMSOL’s solution/
(µH·m−1)Maximum current density/
(109A·m−2)10 1.35489 1.3775 2.1054 15 1.30642 1.3641 2.0103 20 1.28442 1.3455 2.0286 25 1.27027 1.3249 1.9191 30 1.19722 1.2998 1.7920 表 5 不同截面形状下电感梯度与电流密度
Table 5. Inductance gradient and current density under different section shapes
cross section
shapeself inductance
gradient/(µH·m−1)mutual inductance
gradient/(µH·m−1)system inductance
gradient/(µH·m−1)maximum current
density/(109A·m−2)rectangular 2.13226 −0.42392 1.28442 2.0286 convex 2.12950 −0.32325 1.48300 1.9780 concave 2.27081 −0.45296 1.36489 1.8741 -
[1] 马伟明, 鲁军勇. 电磁发射技术[J]. 国防科技大学学报, 2016, 38(6):1-5. (Ma Weiming, Lu Junyong. Electromagnetic launch technology[J]. Journal of National University of Defense Technology, 2016, 38(6): 1-5 doi: 10.11887/j.cn.201606001 [2] 刘明, 舒涛, 薛新鹏. 新型四极轨道电磁发射器[J]. 火力与指挥控制, 2019, 44(3):23-27. (Liu Ming, Shu Tao, Xue Xinpeng. A new four-pole rail electromagnetic launcher[J]. Fire Control & Command Control, 2019, 44(3): 23-27 doi: 10.3969/j.issn.1002-0640.2019.03.004 [3] 任波涛. 四轨电磁轨道炮概要设计与有限元分析[D]. 南京: 南京理工大学, 2011: 16-24.Ren Botao. General design and finite element analysis of four-rail electromagnetic railgun[D]. Nanjing: Nanjing University of Science and Technology, 2011: 16-24) [4] Yang Z Y, Feng G, Xue X P, et al. An electromagnetic rail launcher by quadrupole magnetic field for heavy intelligent projectiles[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1095-1100. [5] Liu S, Miao H, Guan J, et al. Investigation of electromagnetic characteristic in series-connected augmented quadrupole rail launcher[J]. IEEE Transactions on Plasma Science, 2020, 48(1): 299-304. [6] 童思远, 冯刚, 杨志勇, 等. 导弹四级磁场电枢轨道过盈配合参数优化[J]. 强激光与粒子束, 2019, 31:013201. (Tong Siyuan, Feng Gang, Yang Zhiyong, et al. Optimization of interference coordination parameters of the four-stage magnetic field armature rail of missiles[J]. High Power Laser and Particle Beams, 2019, 31: 013201 doi: 10.11884/HPLPB201931.180252 [7] 杨志勇, 冯刚, 童思远, 等. 强脉冲电流四极磁场导轨瞬态动力学分析[J]. 弹箭与制导学报, 2019, 39(3):119-124, 129. (Yang Zhiyong, Feng Gang, Tong Siyuan, et al. Transient dynamic analysis of four-pole magnetic field guide rail with strong pulsed current[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2019, 39(3): 119-124, 129 [8] Novac B M, Smith I R, Enache M C, et al. Studies of a very high efficiency electromagnetic launcher[J]. Journal of Physics D, 2002, 35(12): 1447-1457. [9] Marshall R A, Wang Y. Railguns: Their science and technology[M]. Beijing: China Machine Press, 2004: 22-35. [10] Grover F W. Inductance calculations: working formulas and tables[M]. New York: Dover Publications, 1962: 22-66. [11] Kerrisk J F. Current diffusion and inductance calculations for rail-gun conductors[R]. USA: Los Alamos National Lab, 1981. [12] 周媛, 严萍, 袁伟群, 等. 电磁轨道发射装置中导轨几何参数对电感梯度的影响[J]. 电工电能新技术, 2009, 28(3):23-27, 35. (Zhou Yuan, Yan Ping, Yuan Weiqun, et al. Effect of geometric parameters of guide rail on inductance gradient in electromagnetic rail launcher[J]. Advanced Technology of Electrical Engineering and Energy, 2009, 28(3): 23-27, 35 doi: 10.3969/j.issn.1003-3076.2009.03.006 [13] 刘守豹, 阮江军, 张亚东, 等. 增强型轨道炮电感梯度及其影响因素[J]. 电工电能新技术, 2009, 28(2):50-53. (Liu Shoubao, Ruan Jiangjun, Zhang Yadong, et al. Inductance gradient of enhanced railgun and its influencing factors[J]. Advanced Technology of Electrical Engineering and Energy, 2009, 28(2): 50-53 doi: 10.3969/j.issn.1003-3076.2009.02.012 [14] 童思远, 冯刚, 连仲谋, 等. 四轨电磁发射器电感梯度影响因素分析[J]. 兵器装备工程学报, 2019, 40(12):221-224. (Tong Siyuan, Feng Gang, Lian Zhongmou, et al. Analysis of factors influencing the inductance gradient of four-rail electromagnetic launcher[J]. Journal of Ordnance and Equipment Engineering, 2019, 40(12): 221-224 doi: 10.11809/bqzbgcxb2019.12.043 [15] 杨志勇, 冯刚, 刘瑜倩, 等. 增强型导弹四极场电磁轨道发射器研究[J]. 空军工程大学学报(自然科学版), 2019, 20(3):77-83. (Yang Zhiyong, Feng Gang, Liu Yuqian, et al. Research on enhanced missile four-pole field electromagnetic rail launcher[J]. Journal of Air Force Engineering University (Natural Science Edition), 2019, 20(3): 77-83 [16] 徐蓉, 袁伟群, 成文凭, 等. 增强型电磁轨道发射器的电磁场仿真分析[J]. 高电压技术, 2014, 40(4):1065-1070. (Xu Rong, Yuan Weiqun, Cheng Wenping, et al. Electromagnetic field simulation analysis of enhanced electromagnetic rail launcher[J]. High Voltage Technology, 2014, 40(4): 1065-1070 [17] 贺景瑞, 李小将. 增强型电磁轨道发射器电磁场和电感梯度仿真分析[J]. 兵工自动化, 2016, 37(8):78-82, 86. (He Jingrui, Li Xiaojiang. Simulation analysis of electromagnetic field and inductance gradient of enhanced electromagnetic rail launcher[J]. Ordnance Industry Automation, 2016, 37(8): 78-82, 86 [18] Liebfried O, Schneider M, Stankevic T, et al. Velocity-induced current profiles inside the rails of an electric launcher[J]. IEEE Transactions on Plasma Science, 2013, 41(5): 1520-1525. [19] 王莹, 肖锋. 电炮原理[M]. 北京: 国防工业出版社, 1995.Wang Ying, Xiao Feng. Principle of electric gun[M]. Beijing: National Defense Industry Press, 1995 -




 下载:
下载: