Study on excitation characteristics of high-order mode coaxial multi-gap cavity
-
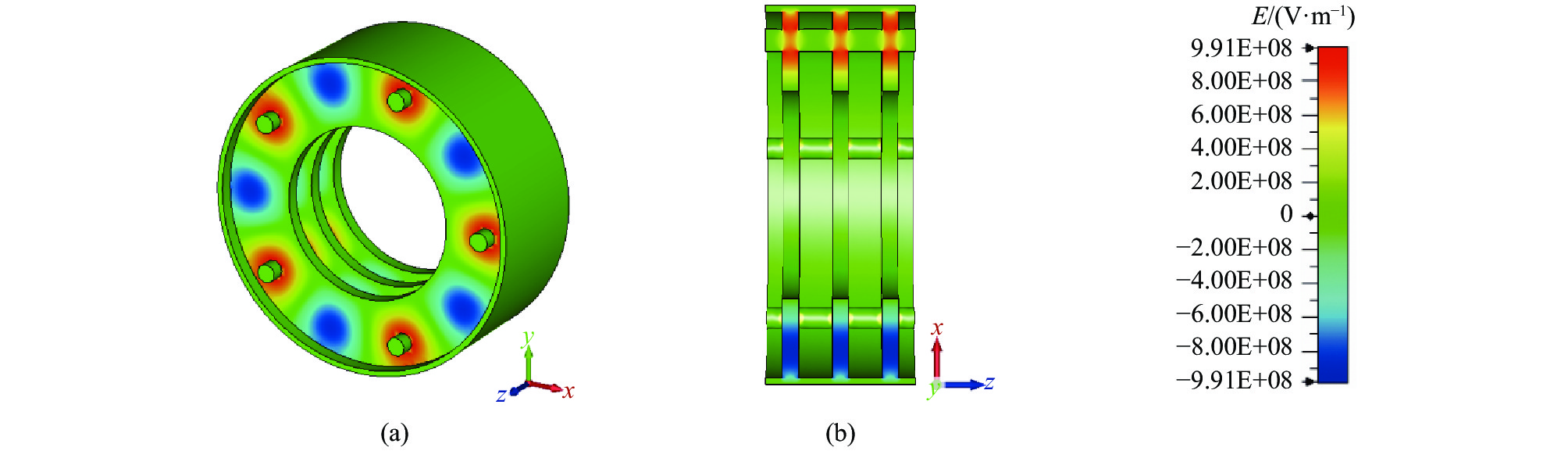
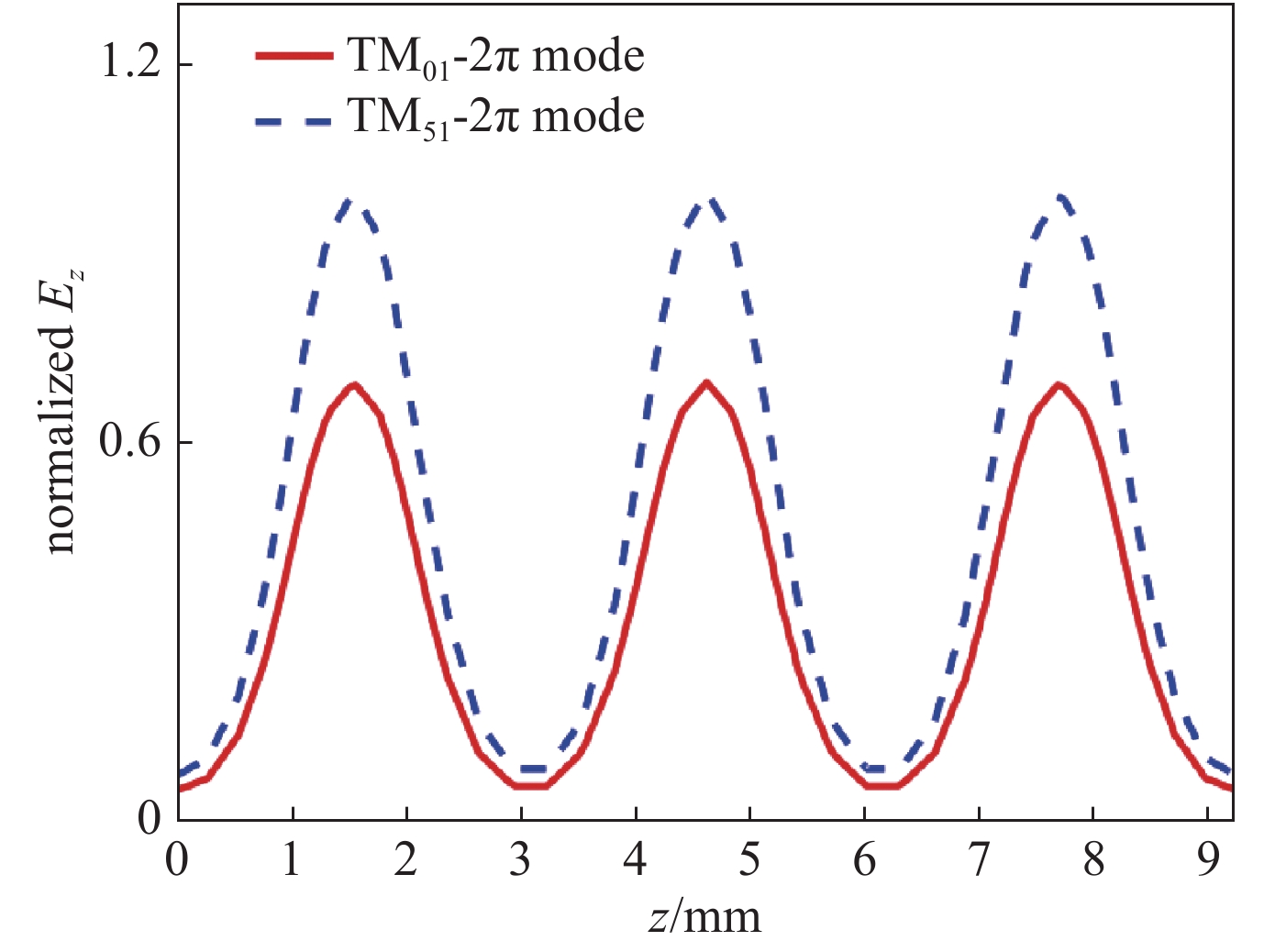
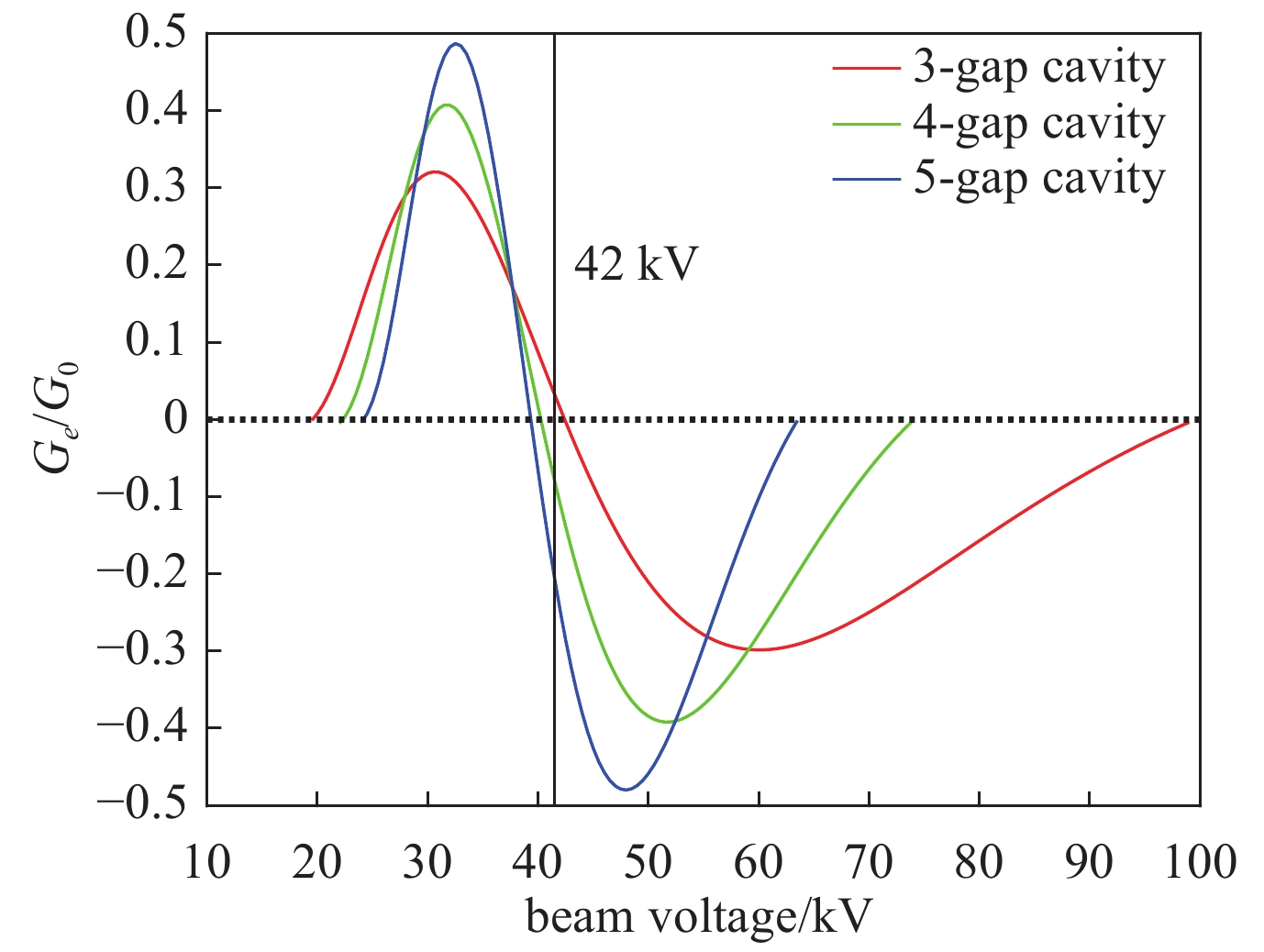
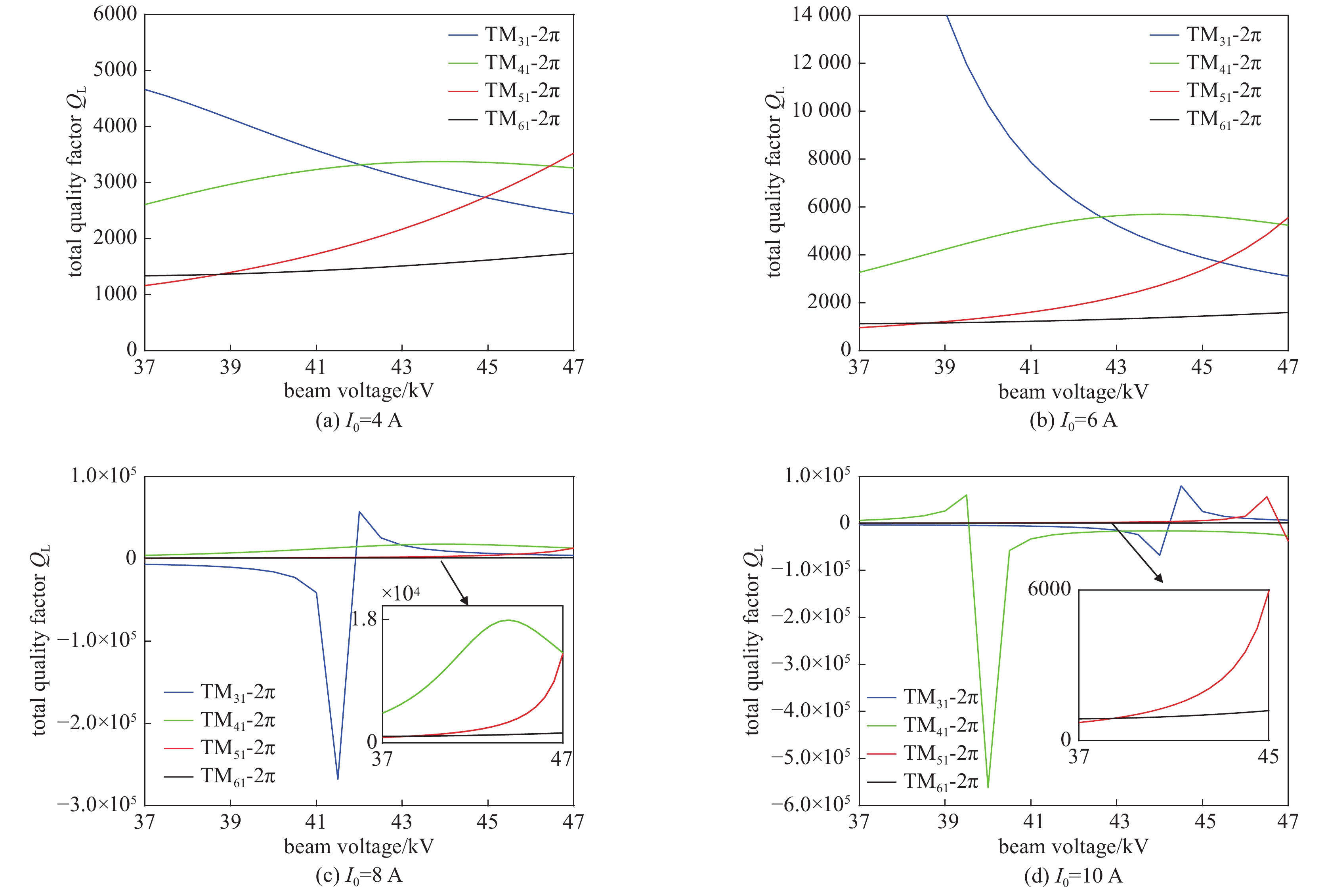
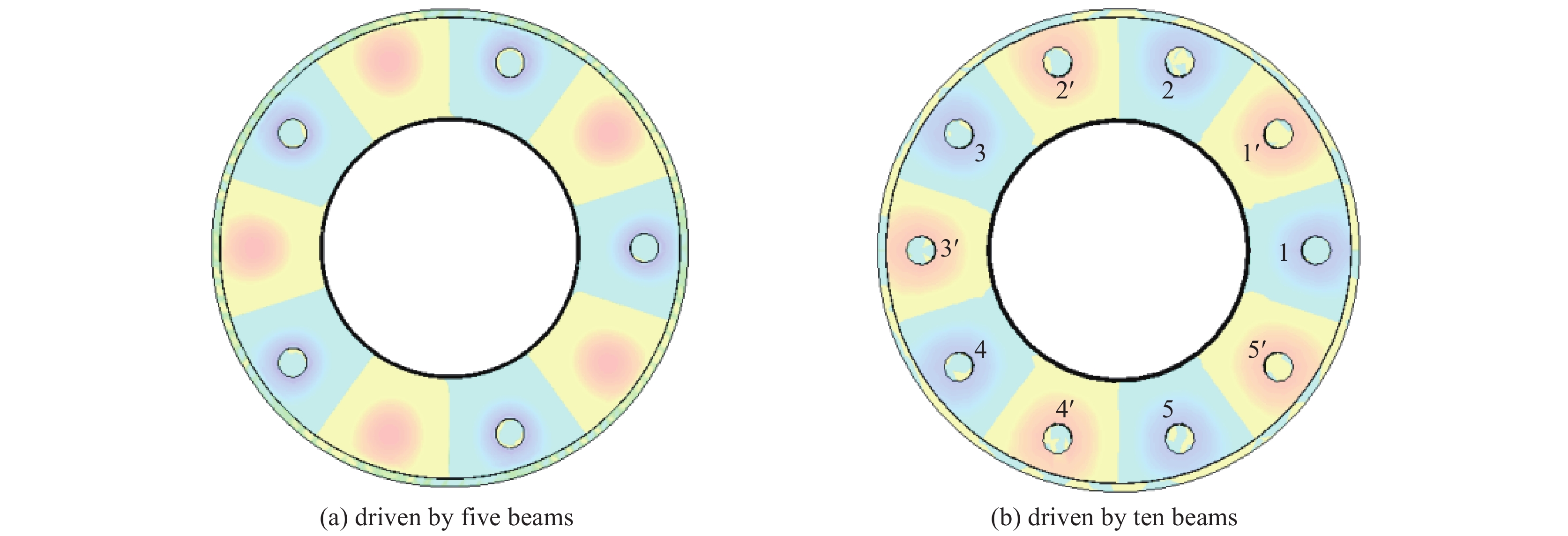
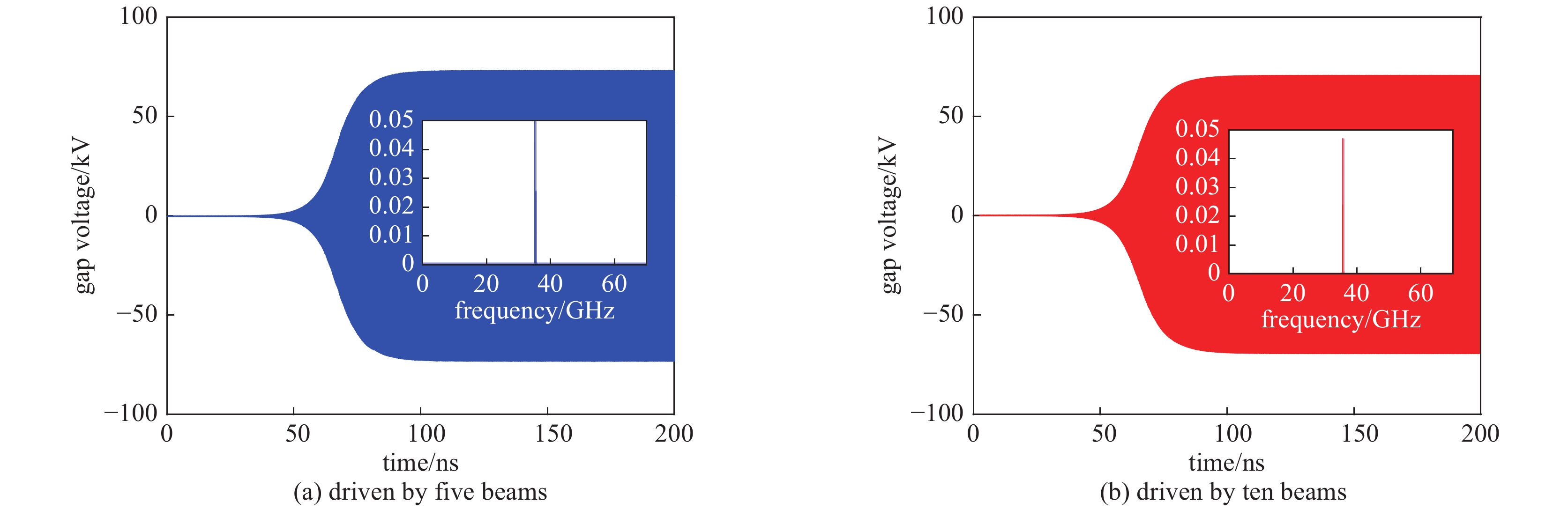
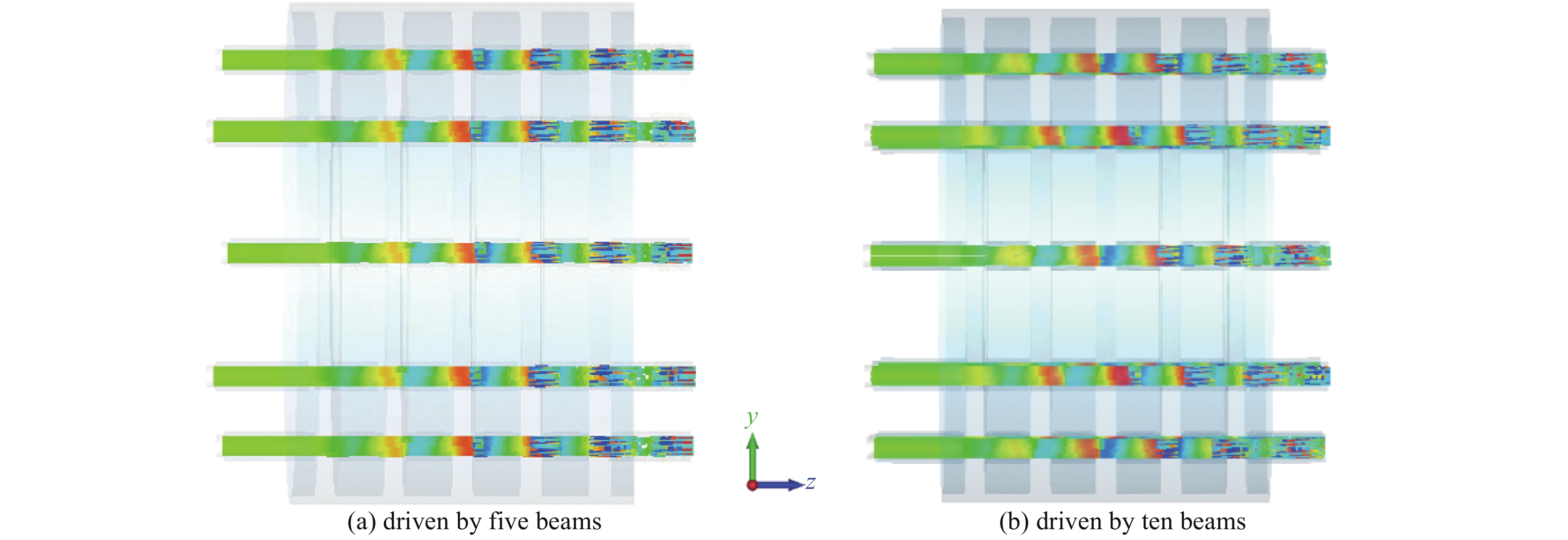
摘要: 提出了一种工作在TM51-2π模式的Ka波段同轴多间隙谐振腔,使用CST本征模求解器研究了此结构的电场分布特性,并分析了基于外侧全通的耦合方式下该结构的冷腔模式特性。在此基础上,通过结合空间电荷波理论和CST三维粒子仿真分析,研究了在多电子注激励下同轴多间隙腔高次模式的起振特性,并分析了此种结构的模式稳定性与注-波互作用特性。研究结果表明:对于工作在Ka波段的TM51-2π模式同轴多间隙腔,采取结构外侧全耦合的方式具有较高的模式稳定性;在此结构中,多电子注不仅会均匀激励起工作模式,也可能非均匀激励起竞争模式;不同于工作在基模的扩展互作用速调管,此种结构的速调管电场极值是分别建立的,因此激励电子注可放置在不同相位的电场极值处;在保持电子注电压、总电流不变的情况下,采取更多电子注的激励方式,需要更小的聚焦磁场。Abstract: This paper proposes a Ka-band coaxial multi-gap cavity operating in the TM51-2π mode. The CST eigenmode solver is used to study the characteristics of the electric field distribution, and the mode characteristics of this cavity have been analyzed based on the all-pass coupling structure at the outer radius. By combining space-charge wave theory and 3-D particle-in-cell (PIC) simulation analysis, this paper studies the start-oscillation characteristics of the high-order mode coaxial multi-gap cavity using the multi-beam excitation method. And it analyzes the mode stability and beam-wave interaction characteristics of the coaxial multi-gap cavity operating in the high-order mode. The results show that the coaxial multi-gap cavity operating in the TM51-2π mode adopting the coupling method at the outer radius possesses high mode stability. In this structure, multiple beams can not only uniformly inspire the operating mode but also non-uniformly inspire the competition mode. Different from the multi-beam extended-interaction klystron (EIK) operating in the fundamental mode, the high-order mode EIK with this structure establishes the gap voltages separately. Therefore, the peak electric fields with different phases can interact with the beams respectively. While keeping the same total beam current and beam voltage, the operating method driven by more beams requires a smaller focusing magnetic field.
-
表 1 工作模式及其相邻模式的频率、品质因数和带宽
Table 1. Frequencies, quality factors and instantaneous bandwidths of the operating mode and its adjacent modes
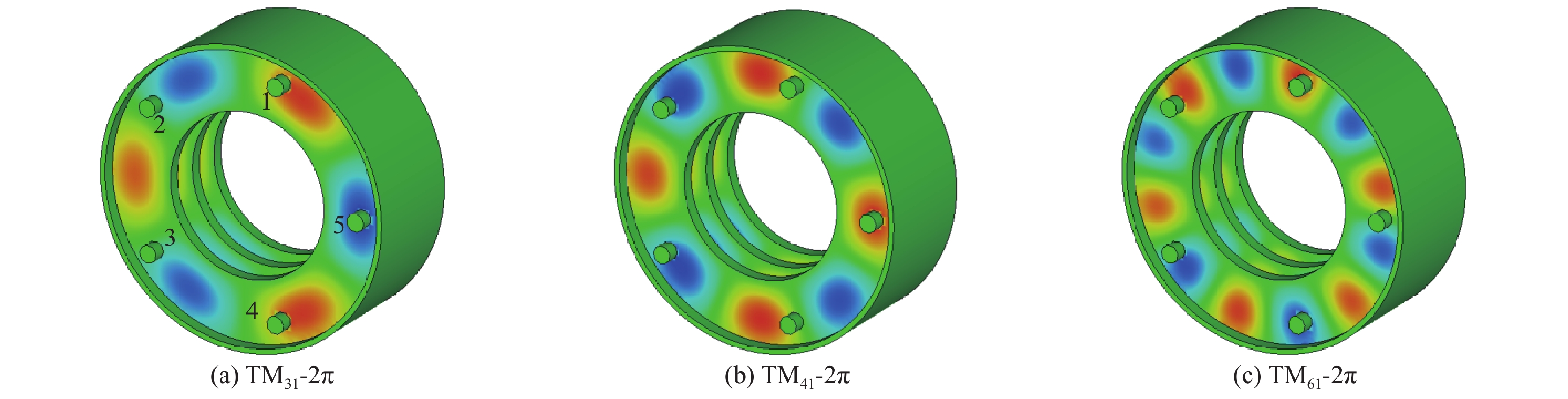
mode f/GHz Q bandwidth/GHz TM31-2π 28.62 1699 0.017 TM31-1/3π 30.46 1675 0.018 TM41-2π 31.58 1850 0.017 TM41-1/3π 33.23 1808 0.018 TM31-2/3π 35.04 1944 0.018 TM51-2π 35.30 2028 0.017 TM51-1/3π 36.74 1963 0.019 TM41-2/3π 37.52 2022 0.019 TM61-2π 38.72 2142 0.018 -
[1] Berry D, Deng H, Dobbs R, et al. Practical aspects of EIK technology[J]. IEEE Trans Electron Devices, 2014, 61(6): 1830-1835. doi: 10.1109/TED.2014.2302741 [2] Pasour J, Wright E, Nguyen K T, et al. Demonstration of a multikilowatt, solenoidally focused sheet beam amplifier at 94 GHz[J]. IEEE Trans Electron Devices, 2014, 61(6): 1630-1636. doi: 10.1109/TED.2013.2295771 [3] Shin YM, Wang J X, Barnett L R, et al. Particle-in-cell simulation analysis of a multicavity W-band sheet beam klystron[J]. IEEE Trans Electron Devices, 2011, 58(1): 251-257. doi: 10.1109/TED.2010.2082544 [4] Nguyen K, Ludeking L, Pasour J, et al. 1.4: Design of a high-gain wideband high-power 220-GHz multiple-beam serpentine TWT[C]// IEEE International Vacuum Electronics Conference. 2010: 23–24. [5] Korolev A N, Zaitsev S A, Golenitskij I I, et al. Traditional and novel vacuum electron devices[J]. IEEE Trans Electron Devices, 2011, 48(12): 2929-2935. doi: 10.1109/16.974731 [6] 丁耀根, 阮存军, 沈斌, 等. X波段同轴腔多注速调管的研究[J]. 电子学报, 2006, 34(s1):2337-2341. (Ding Yaogen, Ruan Cunjun, Shen Bin, et al. Study of a X-band coaxial cavity multi beam klystron[J]. Acta Electronica Sinica, 2006, 34(s1): 2337-2341 [7] Kowalski E J, Shapiro A, Temkin R J. An overmoded W-band coupled-cavity TWT[J]. IEEE Trans Electron Devices, 2015, 62(5): 1609-1616. doi: 10.1109/TED.2015.2407865 [8] Ding Yaogen, Shen Bin, Cao Jing, et al. Research progress on X-band multi-beam klystron[C]//IEEE International Vacuum Electronics Conference. 2008: 421-422. [9] 董玉和. 微波圆柱和同轴腔高阶横磁模式及输出耦合[D]. 北京: 中国科学院电子学研究所, 2006: 21-41.Dong Yuhe. Research on higher order transverse magnetic mode of microwave cylindrical coaxial cavity and its out-coupling[D]. Beijing: Institute of Electronics, Chinese Academy of Sciences, 2006: 21-41 [10] Lü Suye, Zhang Changqing, Wang Shuzhong, et al. Stability analysis of a planar multiple-beam circuit for W-band high-power extended-interaction klystron[J]. IEEE Trans Electron Devices, 2015, 62(9): 3042-3047. doi: 10.1109/TED.2015.2435031 [11] 张克潜, 李德杰. 微波与光电子学中的电磁理论[M]. 2版. 北京: 电子工业出版社, 2001.Zhang Keqian, Li Dejie. Electromagnetic theory for microwave and optoelectronics. 2nd ed. Beijing: Publishing House of Electronics Industry, 2001 [12] 肖宇杰, 林福民. 0.3 THz TM10,1,0模同轴耦合腔链[J]. 强激光与粒子束, 2018, 30:103101. (Xiao Yujie, Lin Fumin. 0.3 THz TM10,1,0 mode coaxial coupled cavity chain[J]. High Power Laser and Particle Beams, 2018, 30: 103101 doi: 10.11884/HPLPB201830.180153 [13] Wang Dongyang, Wang Guangqiang, Wang Jianguo, et al. A high-order mode extended interaction klystron at 0.34 THz[J]. Physics of Plasmas, 2017, 24: 023106. doi: 10.1063/1.4975649 [14] Chodorow M, Wessel-Berg T. A high-efficiency klystron with distributed interaction[J]. IEEE Trans Electron Devices, 1961, 8(1): 44-55. doi: 10.1109/T-ED.1961.14708 [15] Luo Jirun, Cui Jian, Zhu Min, et al. Stability analysis of 2π mode operation in the beam-wave interaction process for a three-gap Hughes-type coupled cavity chain[C]//IEEE International Vacuum Electronics Conference. 2012: 281-282. -





 下载:
下载: