-
氢是元素周期表中最简单的元素，只包含一个核外电子，却拥有非常复杂的高压相图，因而成为现代凝聚态理论、数值模拟方法和高压实验等基础科学研究的重要对象[1-3]。氢还是自然界最丰富的元素，亦是众多天体的重要组成成份[4]，其性质是星体结构、演化、观测等领域长期关注的关键问题[5–6]。氢及同位素更是惯性约束聚变（ICF）[7-9]、国际热核实验堆（ITER）[10]等工程物理设计中的重要材料，特别是在ICF中，因其在内爆、流体动力学不稳定性产生及演化中的决定作用，一直受到特别重视，尤其是最近几年来，随着美国国家点火装置（NIF）[8]研究的深入，持续作为NIF高能密度物理研究的核心对象。这些研究中，氢氘宽区物态方程涉及的物质状态包括固、液、气及等离子体状态[11-13]，在不同的状态下，组成成分包括分子、原子、分子离子、原子离子及电子，属于典型的复杂状态、复杂多粒子体系。一个多世纪以来，氢氘宽区物态方程犹如一颗耀眼的明珠，持续吸引科学家们的注意。科学家们利用多种不断发展完善的理论和实验方法，对氢氘的物态方程及其他相关性质进行了广泛研究[14-72]，文献[32]对其中的大部分理论工作进行了综述分析。本文结合近几年新发表的NIF实验结果[3, 30, 33-34, 55]，对氢氘宽区物态方程进行进一步的综述分析。在文献[32]数据分析与评估基础上，构建了氢氘的宽区物态方程，并利用已有实验和理论结果对氢物态方程进行验证，也给出氘物态方程的主雨贡纽（一次冲击雨贡纽）、二次冲击雨贡纽数据与国外最新实验结果的比较。最后指出了未来需要关注的研究方向。
-
天体问题和ICF研究关心宽区物态方程，特别是在ICF过程中，氘氚燃料经历的热力学范围广，温度从临界温度到上亿℃、密度从临界密度到几kg·cm−3，这种宽热力学区域的变化给实际工程可用的宽区理论物态方程构建带来极大困难。
迄今为止，国内外氢及同位素的宽区物态方程研究大致可分为两类。第一类是采用半经验模型：按不同热力学区域的相结构进行建模并分别计算不同相的物态方程，基于化学图景，计算离化和电离系统的性质，利用实验数据进行定标；对化学组分不是很明确的区域，采用基于物理图景的量子分子动力学（QMD）和直接量子蒙特卡罗（QMC）方法模拟获得理论数据；综合理论、实验和数值模拟结果，形成多模型集成的理论框架，以数据库或解析理论模型表示。第二类则完全基于物理图景，采用QMD和QMC模拟获得宽区域理论数据，以数据库或拟合函数表示。第一类的代表包括美国Kerley等构建的SESAME[16-17]，Saumon等构建的SCvH[19-20]、德国Nettelmann等构建的REOS[18]数据库、前苏联Trunin等构建的宽区物态方程[22]、中国刘海风等构建的WEOS[12]。第二类的代表包括法国Caillabet等基于第一原理数值模拟构建的氢多相物态方程[21]、美国胡素兴等发表的约束路径积分蒙特卡罗（RPIMC）模拟数据库[11]、中国王聪等发表的密度泛函（DFT）数据库[23]。由于覆盖热力学区域的范围宽，并得到了比较充分的实验验证，工程实际应用多采用第一类宽区物态方程，第二类宽区物态方程作为验证和评估数据。
文献[33-34]简要介绍了美国用于行星科学和ICF研究的几个物态方程模型，并将这些物态方程模型的计算结果与Omega激光装置上的最新冲击压缩实验结果进行了对 比，如图1和图2所示。图1展示了1980年以来美国[3, 26, 29, 31, 33, 56]、俄罗斯[28]利用化爆、轻气炮、球面汇聚、磁和激光驱动获得的主雨贡纽实验数据，也展示了SESAME数据库等多个理论模型计算的雨贡纽曲线。图2展示了与图1类似的实验结果和更为丰富的理论雨贡纽曲线，同时也清晰描绘了NIF几个实验装置液氘燃料的一次冲击状态。将众多理论、高精度实验数据放在一起的详细对比尚属首次，文章中有些理论结果或者观点，在过去的资料中从没有出现过。分析认识这些数据，有利于我们了解美国NIF研究的物态方程基础，也可以更好地评判我们自己的工作，为未来ICF理论研究提供强有力的支撑，这也是写作本文的最主要动机。结合图1和图2、文献[33-34]的内容和我们对氢氘物态方程的理解，一些分析判断如下：
图 2 实验与理论模型预测的低温液氘雨贡纽数据比较[34]
Figure 2. Summary of experimental data on the pressure-density compressibility along the cryogenic Hugoniot for D2，along with several EOS model predictions
（1）NIF计划中ICF最常用的物态方程是LEOS1014，也即通常所说SESAME2003[16]。从了解到的情况可知，SESAME2003沿袭了早期1972版本[17]的化学模型理论框架，改进了液体微扰论、分子振动和转动、离化平衡处理方法，采用现代密度泛函理论数值模拟结果和新的实验数据进行了定标，氘物态方程数据库的密度范围为0～100 g/cm3，温度范围为5～108 K，只对有限学术团体公开。
（2）基于QMC和QMD的完全第一原理物态方程数据库，即胡素兴的列表数据不能满足实际问题模拟，文献[34]明确指出其在1000 K以下切换为SESAME1972。
（3）文献[33]将多种理论模型[11, 15-16, 18-21]与最新实验数据进行了对比。在我们看来，这些对比至少存在两点不妥，一是关于Cailiabet模型的应用超出了作者说明的范围[21]，与高压数据作对比并不合理，二是FPEOS2011即胡素兴的数据表温度、密度范围[21]有限，用于图1雨贡纽计算的初始状态不明确。
对宽区物态方程研究而言，雨贡纽曲线是其曲面上最重要的特征线，也是实验和理论互为验证的最关键数据之一。长期以来，氢及同位素氘的雨贡纽是其物态方程研究的核心问题。Zeldovich[71]从基本理论出发，分析给出单原子和双原子理想气体的一次冲击极限压缩比分别为4和6。对实际气体压缩过程而言，理想气体近似并不成立。由于压缩过程中粒子间相互作用增强或粒子内部自由度先后激发，导致实际的一次冲击压缩极限偏离理想值较远[68, 72]。为了研究真实稠密流体氢氘的压缩性质，科学家们探索了多种动静态加载技术和不同层次的物理建模[32, 70-71]。图1和图2展示了一些典型的代表性结果，这些结果的产生时间基本代表了当时的实验和理论研究能力。氘的极限压缩比究竟是4.5还是6，曾经是非常热门的研究课题[32,72]，目前的理论及实验研究已经有明确定论，在4.5附近。
-
构建氢宽区物态方程，建立或选取合适的物理模型是解决宽区物态方程理论描述困难的必经之路。尽管当前实验、数值模拟技术已有长足发展，氢的离解、电离和绝缘体到金属的转变定量描述仍是尚未解决的科学难题[3, 47, 70-71]。在数据库的构建中，弱化对相变及相界附近状态量的定量描述要求，针对氢分子、原子、等离子体状态的统一描述，发展了改进的自由能模型[35-36]。针对粒子类型及相互作用复杂的温稠密状态，通过第一性原理模拟与数据评估选取模型[37-42]。针对冰气共存状态，采用多参数模型[43-45]。
-
化学自由能模型假设物质是由可区分的分子、原子、离子和电子组成，粒子之间具有各种相互作用。通过物理及数值分析方法可获得自由能函数的解析表达式，包括平动能、相互作用能、内部激发能等。各种粒子的平动能计算方法与理想气体相同，其中复合粒子遵守麦克斯韦-玻耳兹曼统计，电子遵守费米-狄拉克统计。带电粒子的库仑能基于点离子近似采用了完全电离等离子体的研究结果。中性复合粒子之间的相互作用能采用液体变分微扰理论处理。带电粒子的有限体积效应采用刚球模型描述。根据化学势平衡条件确定平衡态粒子组分和自由能，并由自由能导出氢的物态方程。为与其他文献自由能模型相区别，以下简称改进的自由能（MFE）模型。
-
Caillabet[21]考虑了氢的固相和液相结构的不同建模及物理极限，利用第一原理分子动力学和耦合量子蒙特卡洛模拟结果标定了模型参数，适用密度范围0.2～5.0 g/cm3、温度高至116 045 K。以下简称第一原理（FP）模型。文献[32]利用多组QMD和QMC模拟结果对其进行了评估，结果表明FP模型在其适用范围内具有较高的置信度。
-
Span[43]以N2为例给出了多参数模型，对N2而言，适用温度范围为63～1000 K，压力低于2.2 GPa。Leachman[44-46]在此基础上，建立了氢氘（Para，orthohydrogen，normal）的多参数模型，基于量子对应态原理和p-ρ-T、饱和蒸汽压、声速、第二维力系数、第三维力系数等多类精密实验数据，经过复杂回归得到了多参数模型数据。实际工程问题中，氢以标准形式存在，本文数据库的构建采用标准氢参数。以下简称此为多参数（MP）模型。文献[69]给出了一种核量子效应修正的方法，这个方法不能准确描述低温、低密度区域氢及同位素的量子效应，以实验为基础的多参数模型则是较好的选择。
-
三个模型的适用区域主要做如下考虑：原模型适用范围、模型之间压强和能量等物理量的衔接。图3给出MFE和MP模型在1000 K以内的压强和能量相对偏差。可见300 K＜T＜1000 K，MFE与MP数据符合较好，即改进的自由能模型可以替代多参数模型；300 K以下大部分区域，MFE和FP相对偏差大多在50%以上，见黑色或灰色区域，即MFE不能描述MP的结果，考虑到MP在该区域的准确性更高，低温下优先选取MP模型。随密度增加，MFE与MP模型呈现明显不同的变化趋势，结合高密度下理论计算与实验结果分析，首先确立了MFE与MP换段的温度、密度区域。
图 3 MFE和MP模型的压强和能量相对偏差
Figure 3. Relative differences of equation of state (EOS) for hydrogen between MFE and MP models
进一步，采用如上方法，确定了MFE和FP模型适用的最佳区域，如图4所示；以MP能量为基准，在密度衔接点处分别对齐不同模型能量；对不同模型密度和温度衔接点附近的能量和压强进行局部光滑化，实现不同物理量的光滑过渡。图5给出密度0.3 g/cm3处光滑处理前后压强和能量的比较情况，多数情况下，光滑前后物理量的相对偏差在±10%以内。
图 4 氢的WEOS模型分区示意图
Figure 4. Constituents of model for hydrogen wide-range EOS (WEOS)
图 5 光滑处理前后压强和能量的对比较
Figure 5. Comparison of equation of state for hydrogen before and after smoothing
按以上方法，实现了对氢宽区域、多状态的物态方程合理描述，获得了温度为20～108 K、密度在10−7～2000 g/cm3范围内的氢宽区物态方程数据库WEOS2018。类比以上过程，构建氘的宽区物态方程。此类物态方程以下简称WEOS。
-
构建的氢宽区物态方程是否能合理描述实验和理论数据、描述的准确程度有多高是数据库应用者关心的实际问题。
为实现尽可能宽区域的描述，胡素兴[11]利用RPIMC方法计算了氘的物态方程数据库，密度、温度范围分别为0.002 g/cm3≤ρ≤1596 g/cm3，1.35 eV≤T≤5.5 keV，简称RPIMC数据库。王聪等人[23]利用QMD和无轨道分子动力学（OFMD）两种模拟方法计算了氢物态方程数据库，密度、温度范围分别为9.82×10−3～1.347×103 g/cm3，1.564×104～5.004441×107 K，简称DFT数据库。这两个数据库均缺104 K以下的数据，不能直接满足ICF等实际问题的模拟需求，文献[34]提到胡素兴的列表数据在1000 K以下切换为SESAME1972，就是这个意思。Nettelmann[18]公开发表的H-REOS3数据库，所用思想与本文类似，即采用分区细化物理建模，综合集成FVT/FVT+，SCvH和Chabrier-Potekhin等多个模型，实现宽区域的描述，密度、温度范围分别为3.0×10−8～1.8×103 g/cm3、60～107 K，简称REOS。
-
WEOS与RPIMC和DFT数据库的压强和能量相对偏差分别见图6、图7。图6可见，T＞105 K范围内，WEOS与RPIMC大部分区域内状态量相对偏差2%以内，在105 K附近及以下，与RPIMC计算结果相对偏差较大；图7 WEOS与DFT数据压强的相对偏差类似，能量的相对偏差在蓝色区域较大，分析是由于DFT数据库模拟采用了QMD和OFMD两种方法，能量零点不同所致。
图 6 WEOS氢数据库与RPIMC数据[11]的压强和能量相对偏差
Figure 6. Relative differences of equation of state for hydrogen between RPIMC and WEOS
图 7 WEOS氢数据库与DFT数据[23]的压强和能量相对偏差
Figure 7. Relative differences of equation of state for hydrogen between DFT and WEOS
-
WEOS与REOS对比如图8所示，结果表明改进的自由能模型能覆盖REOS中FVT/FVT+，SCvH和Chabrier-Potekhin等三个模型，精度相当，有效避免了多模型衔接带来的能量不连续问题，具备更好的普适性。
图 8 氢WEOS数据库与H-REOS3数据库的压强和能量相对偏差
Figure 8. Relative differences of equation of state for hydrogen between REOS and WEOS.
-
利用WEOS和REOS数据库，分别计算了氢的雨贡纽（初态温度20 K，密度0.071 g/cm3）、300 K声速、300 K等温线及冷压曲线，结果如图9～图12所示，可见由于REOS数据点稀疏，雨贡纽和声速存在锐点，WEOS数据连续性更好，由其计算的声速比文献的结果更符合实验[48]。300 K等温线与实验[49–51]、冷压与CEIMC[52]，DFT[53]计算结果相比，WEOS数据相对偏差约在5%以内。图9还画出了更早的液体氢的实验数据[54–55]，可见WEOS可准确描述几个GPa冲击压强下的实验数据。
Loubeyre[30]和Brygoo[55]分别于2012年和2015年发表了在OMEGA装置上的23发液氢的预压缩冲击雨贡纽实验，实验样品初始温度297 K，直接测量样品压强，压强测试不确定度0.03 GPa，然后由室温等温线物态方程计算密度，如表1所示。由表1室温及对应密度，采用WEOS数据库等物态方程计算的对应23个样品压强见表1所示，可见WEOS数据库计算的压强与实验结果相符，与MP相当，相对偏差约2%，REOS相对偏差约10%，FP相对偏差约20%，低密度处FP相对偏差更大一些。雨贡纽反映冲击加载下初态和末态之间的关系，初始状态量的准确计算对高精度数据分析而言，是非常重要的。
表 1 OMEGA装置预压缩氢实验样品初态及不同物态方程计算结果
Table 1. Initioal state of pre-compression hydrogen：experimental data on OMEGA and results from different models
shot ρ0/（104 g·cm−3） p0/GPa p0WEOS/GPa p0MP/GPa p0FP/GPa p0REOS/GPa 34834 881±36 0.31 0.30785 0.30786 0.28581 0.2794 34835 754±46 0.22 0.21811 0.21811 0.26239 0.2003 36174 1216±19 0.70 0.70278 0.70268 0.54969 0.6477 36176 1241±18 0.74 0.74458 0.74452 0.58391 0.6872 38326 576±68 0.13 0.12936 0.12936 0.26881 0.1210 38991 1204±19 0.68 0.68338 0.68334 0.53405 0.6294 38997 644±59 0.16 0.15893 0.15893 0.26314 0.1476 39000 1575±10 1.48 1.51504 1.56795 1.27030 1.4040 41451 1561±11 1.44 1.47493 1.52092 1.23248 1.3660 41458 644±59 0.16 0.15893 0.15893 0.26314 0.1476 43297 869±37 0.30 0.29825 0.29825 0.28216 0.2710 43298 1535±11 1.37 1.40234 1.43708 1.16443 1.2970 47716 644±59 0.16 0.15893 0.15893 0.26314 0.1476 47719 829±40 0.27 0.26800 0.26800 0.27231 0.2444 52250 893±35 0.32 0.31772 0.31772 0.28980 0.2881 53835 869±37 0.30 0.29825 0.29825 0.28216 0.2710 53838 644±59 0.16 0.15893 0.15893 0.26314 0.1476 55003 869±37 0.30 0.29825 0.29825 0.28216 0.2710 56366 1571±10 1.47 1.50350 1.55438 1.25941 1.3930 50377 869±37 0.30 0.29825 0.29825 0.28216 0.2710 53471 644±59 0.16 0.15893 0.15893 0.26314 0.1476 53472 869±37 0.30 0.29825 0.29825 0.28216 0.2710 53478 905±34 0.33 0.32785 0.32785 0.29413 0.2970 利用WEOS数据库，以上述状态为初态，分别计算了初始压强为0.16，0.3，0.7，1.5 GPa的室温预压缩氢的雨贡纽数据，图13和图14分别给出理论p-σ及T-p和实验数据的对比。为使结果更清晰，且画图方便，图中仅画出了0.16，0.3，0.7，1.5 GPa四个压强附近的实验，即初态0.16 GPa的雨贡纽实验包括了初始压强为0.13 GPa的一个数据，1.5 GPa理论数据对应的实验初始压强在1.37～1.48 GPa之间，其他两个初始压力的实验情况类似，同一实验数据的不确定度均取文献中的最大值。实验初始状态见图中文字和颜色所示，图23中的空心[30]符号对应激光压缩实验早期处理结果，实心[55]符号对应对石英基板的预压缩状态进行修正后的结果。压强、密度图同时呈现2012年和2015年的结果，温度、压强图只画出2015年的结果。可见，在实验不确定度范围内，预压缩实验很好地验证了WEOS的计算结果，且修正后的实验结果与WEOS理论结果更相符。相对而言，初态0.16 GPa的雨贡纽实验与理论计算结果偏离较大。实验采用红宝石荧光法测量初始压强，实验初始压强的测试不确定度为0.03 GPa，在低压如0.16 GPa处，相当于压强测量相对偏差约19%，这种偏差是否是造成0.16 GPa理论与实验偏离较大的原因呢？为给出压强不确定性对理论计算结果影响的直观图像，图13中也画出0.13 GPa初始压缩状态的雨贡纽曲线，如虚线所示，虚线与实验数据更接近一些，但是仍然不能解释初态0.16 GPa的雨贡纽实验与理论计算结果偏离较大的原因。这个分析告诉我们，一方面初始压强的测量精度提高对分析实验数据是有利的，另一方面，实验数据分析所用低压初始理论数据或者WEOS理论数据在这个区域仍有提升精度的空间，这是未来值得考虑的问题。图14可见，冲击温度除两个冲击加载压力低于25 GPa的数据外，理论结果与大部分实验相符。
-
由氘的宽区物态方程计算的主雨贡纽和二次冲击雨贡纽压强-压缩比关系如图15和图16所示，并与实验[3, 26, 33, 56]作对比。图15可见，20 GPa以内与高精度的气炮实验[26]结果一致，30～140 GPa与高精度的磁驱动实验[3]结果一致，80～550 GPa与最新的激光实验[33]一致。图16可见，四发二次冲击雨贡纽实验中三发数据在实验不确定度范围内与理论一致，一发例外。Fernandez[33–34]给出了多个国外理论模型[11, 15–16, 18, 20–21, 24]与实验的对比，见图1，同时也分析了理论模型预测的二次冲击数据与实验的对比情况，详见原文图4，认为62 GPa起始的二次冲击理论与实验一致，大于175 GPa的三发实验比RPIMC[11]，LEOS 1013[15]，LEOS 1014[16]，SESAME 5267[20]，FPEOS[21]等多个理论预测结果高约5%～8%。图15和图16给出WEOS理论数据与实验的对比情况，可见除序号为82518（一次冲击204.6 GPa）和82526（一次冲击225.16 GPa，二次冲击742.82 GPa）两发实验外，宽区理论模型预测结果均与实验结果完美吻合，得到了气炮、激光和磁驱实验验证，相比Fernandez[33]用到的Kerley[16]，Sesame 5267[20]，Caillabet[21]，FPEOS[11]等几个模型，本文宽区模型与实验吻合最好。这是个非常令人兴奋的对比结果。液氘的实验数据非常多，但由于实验精度不同，图15中仅画出了目前认为精度最高的四组国外数据，也标上我国黄秀光等[57]的实验结果作为对比。由于实验数据来源比较多，理论与实验数据的对比一定要十分谨慎，数据分析中发现初始密度对结果的影响比较明显，不同实验数据的换算需要关注其标称初始密度。
-
用于宽区物态方程数据库验证的理论和实验温度、密度状态点如图17所示，实验研究充分的区域是实线蓝色方框区域、室温等温线（湖蓝色线）、液氢一次冲击压缩（绿色实线）、室温预压缩氢一次冲击压缩（红色和蓝色实线）附近区域，另有偏离这些区域不太远的少量多次冲击压缩实验。数值模拟状态点见图17中的加号和乘号等符号、零温压强（蓝色三角和粉色实线）所示。WEOS数据与多个模拟及实验数据的对比表明在蓝色虚线所示的区域，多个数值模拟结果与WEOS理论数据之间还存在较大的相对偏差，需要发展新的数值模拟及实验验证方法，在蓝色点线所示的区域，量子效应非常重要，仍缺乏有效的实验印证，理论研究也不够充分。国外资料也已表明NIF已将低温氢氘的问题列为未来十大科学发现实验之一。未来可根据应用情况和实际需求，在这些区域开展更为深入的研究工作。
-
本文综述了国内外氢及同位素氘宽区物态方程研究进展。结合以前的数据评估，构建了氢的宽区域物态方程数据库WEOS，数据库适用的温度、密度范围分别为20～108 K，10−7～2000 g/cm3。数据库得到多个研究小组的理论与实验结果验证。采用类似方法构建了氘的宽区域物态方程，结果表明新构建的氘WEOS与气炮、激光、磁驱等实验的吻合度比国外现有文献模型更好，可作为ICF等理论研究精密数据使用。
致 谢 氢氘宽区物态方程构建直接用到了多参数模型、第一原理模型，特别致谢来自美国爱达荷大学应用热力学研究中心的Leachman教授，来自华盛顿大学能源实验室的Richardson教授和来自法国原子能武器实验室CEA的Caillabet教授的工作。氢的物态方程研究具有很长的历史，谢谢为此付出努力的各国先辈们。
Progress on wide-range equation of state for hydrogen and deuterium
-
摘要: 氢是自然界最丰富的元素，是天体物理和惯性约束聚变（ICF）研究的重要对象。简要综述了国内外氢及氘宽区物态方程研究进展，特别评述了OMEGA激光装置上的最新冲击压缩 实验和理论模型的对比分析情况。在以往数据分析评估基础上，利用改进的化学自由能模型、第一原理数值模拟结果及多参数物态方程模型，构建了氢的宽区物态方程，适用温度、密度范围分别为20～108 K，10−7～2000 g/cm3。与已有多类实验如冲击压缩实验、静高压等温线实验、声速等实验结果对比表明，新构建的氢宽区物态方程具有较高的置信度，为天体物理、惯性约束聚变、国际热核实验堆等工程物理设计提供高精度的支撑数据。氢宽区物态方程的构建及验证方法亦可适用于其同位素氘，该方法构建的氘宽区物态方程与2019年最新发表的主雨贡纽、二次冲击雨贡纽数据的吻合程度明显优于当前国外模型。指出了未来研究需要关注的状态区域。Abstract: Hydrogen is the most abundant element in nature and an important object of astrophysics and ICF research. This paper briefly presents an overview of the research progress in wide-range equation of state and especially comments assessment of the most recent shock compression experiments on Omega laser facility and the theoretical models. Based on the previous work, the wide-range equation of state of hydrogen is constructed by using the improved chemical free energy model, the first-principle numerical simulation results and the multi-parameter equation of state model, which is applicable in the temperature range of 20−108 K and the density range of 10−7−2000 g/cm3. Compared with experimental results, such as those of shock compression experiment, static high pressure isotherm experiment and sound velocity experiment, the newly-constructed wide-range equation of state for hydrogen has high confidence and provides high precision data for astrophysics, inertial confinement fusion, international thermonuclear experimental reactor and other engineering physics designs. The construction and validation method of the hydrogen wide-range equation of state can also be applied to its isotope deuterium. In comparison with current models published abroad, the deuterium wide-range equation of state constructed by this method is in better agreement with the experimental data of principal and secondary Hugoniot published in 2019. This paper also points out the temperature-density regimesthat need attention in future research.
-
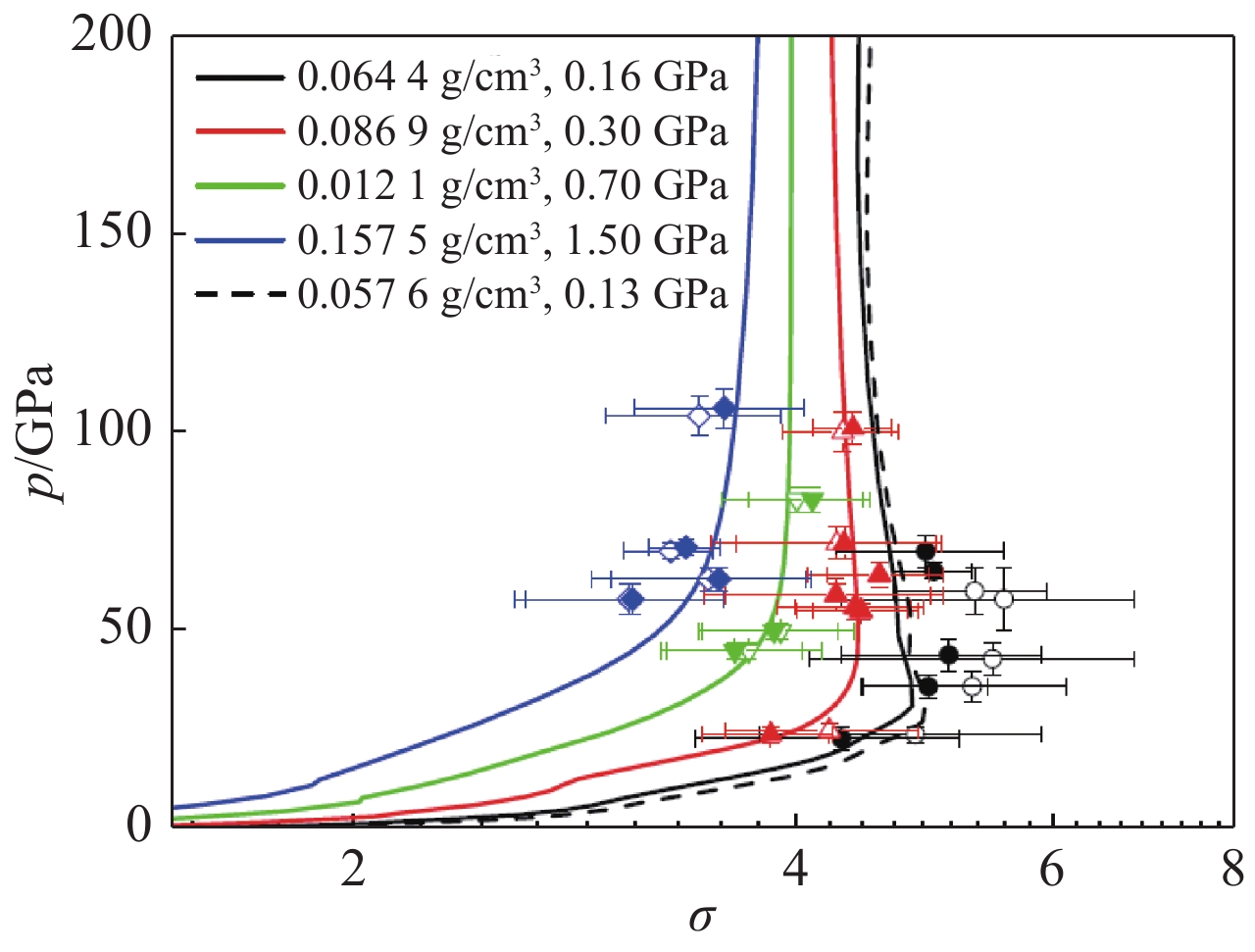
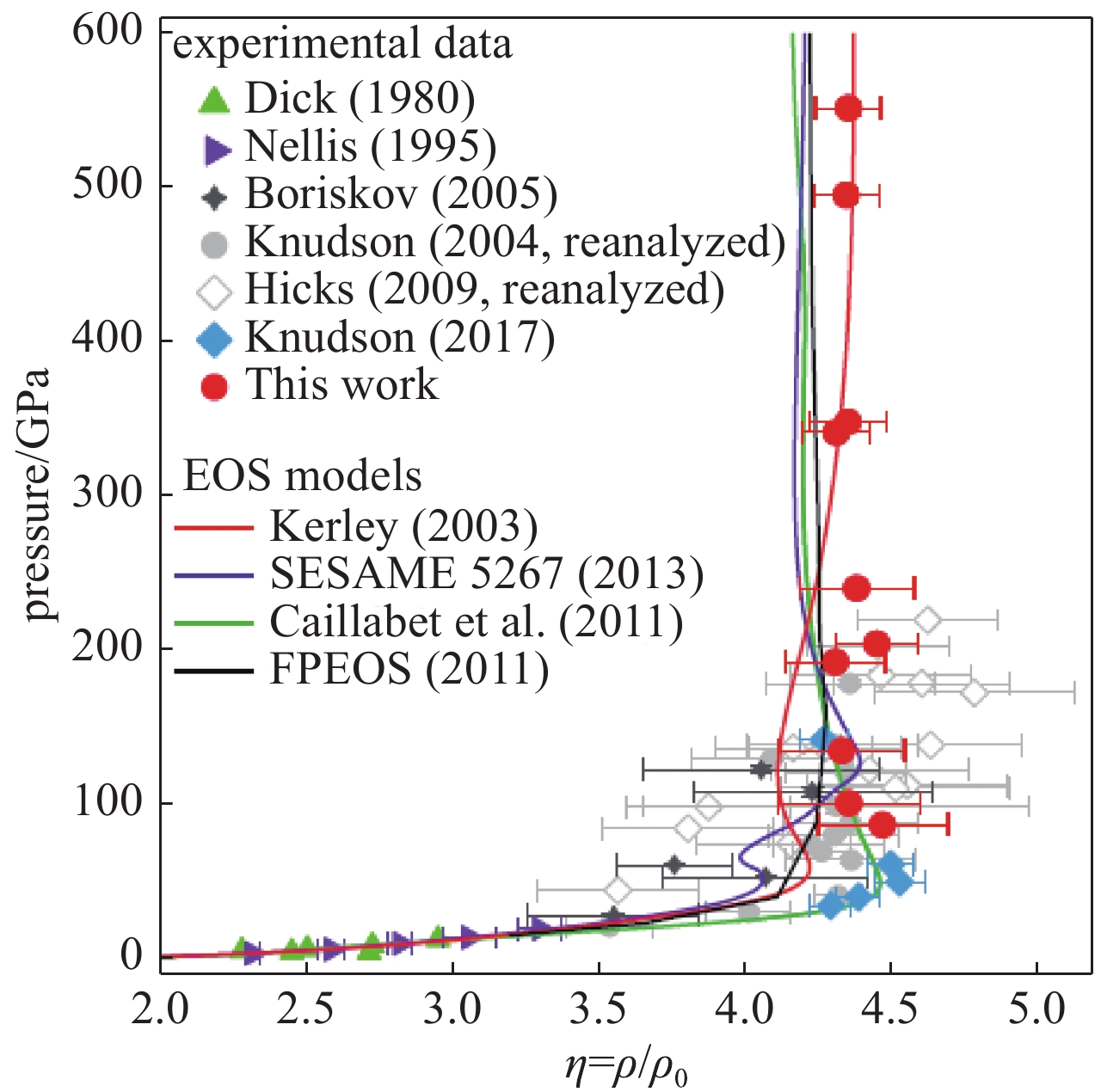
图 2 实验与理论模型预测的低温液氘雨贡纽数据比较[34]
Figure 2. Summary of experimental data on the pressure-density compressibility along the cryogenic Hugoniot for D2，along with several EOS model predictions
图 3 MFE和MP模型的压强和能量相对偏差
Figure 3. Relative differences of equation of state (EOS) for hydrogen between MFE and MP models
图 5 光滑处理前后压强和能量的对比较
Figure 5. Comparison of equation of state for hydrogen before and after smoothing
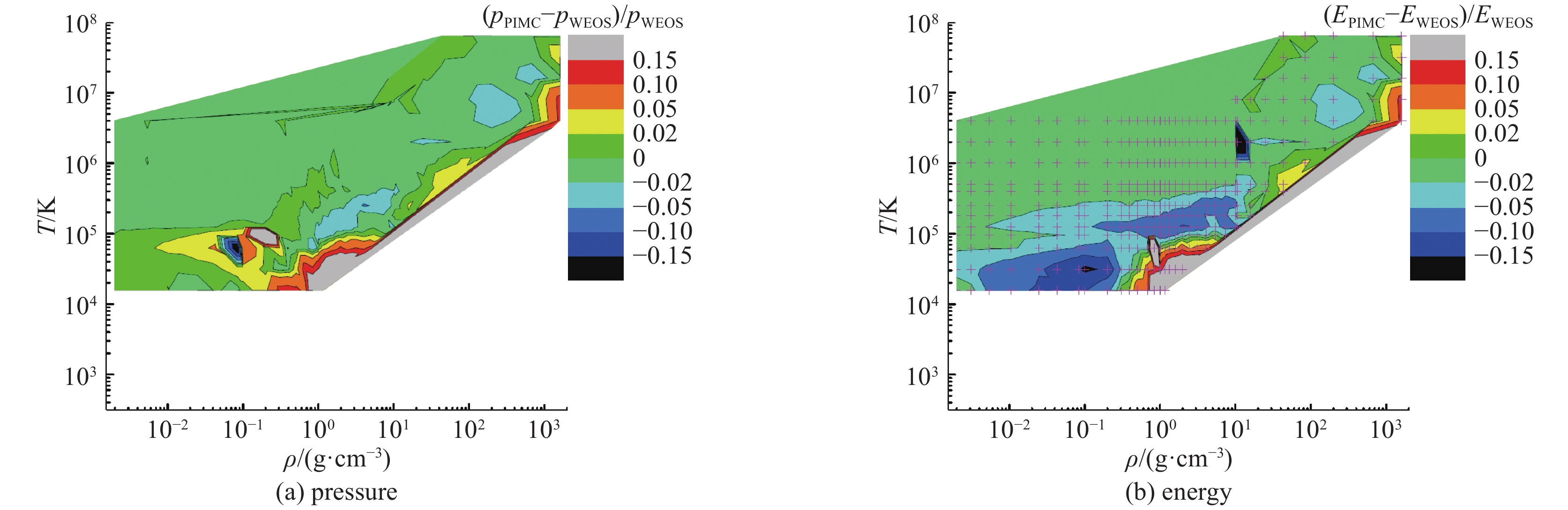
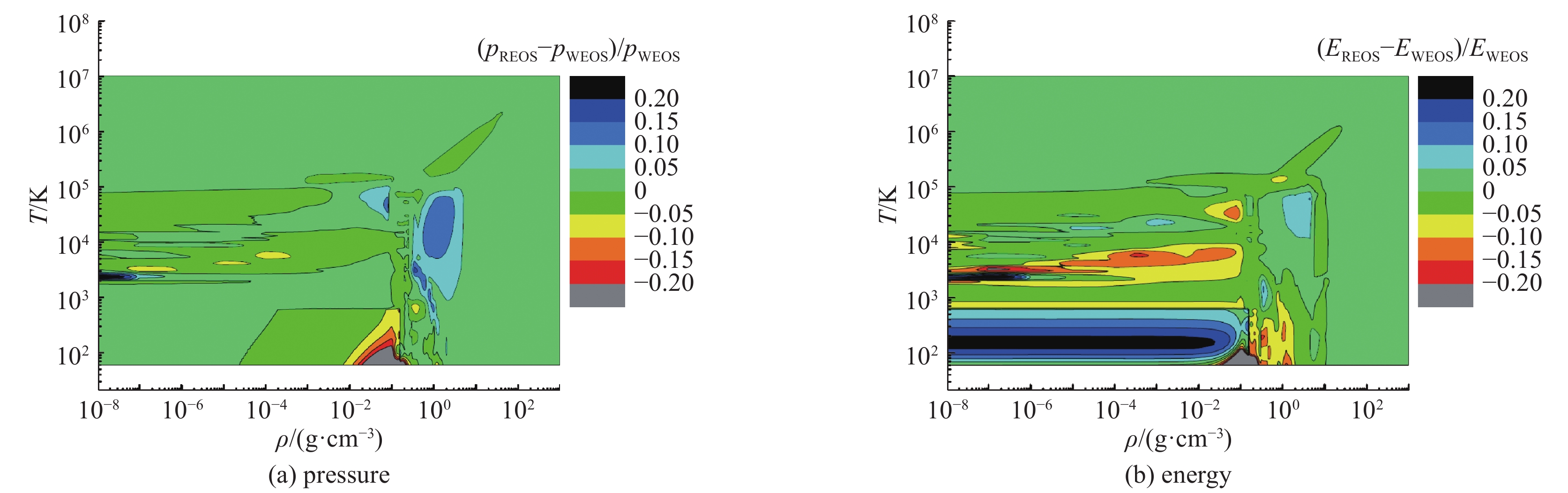
图 6 WEOS氢数据库与RPIMC数据[11]的压强和能量相对偏差
Figure 6. Relative differences of equation of state for hydrogen between RPIMC and WEOS
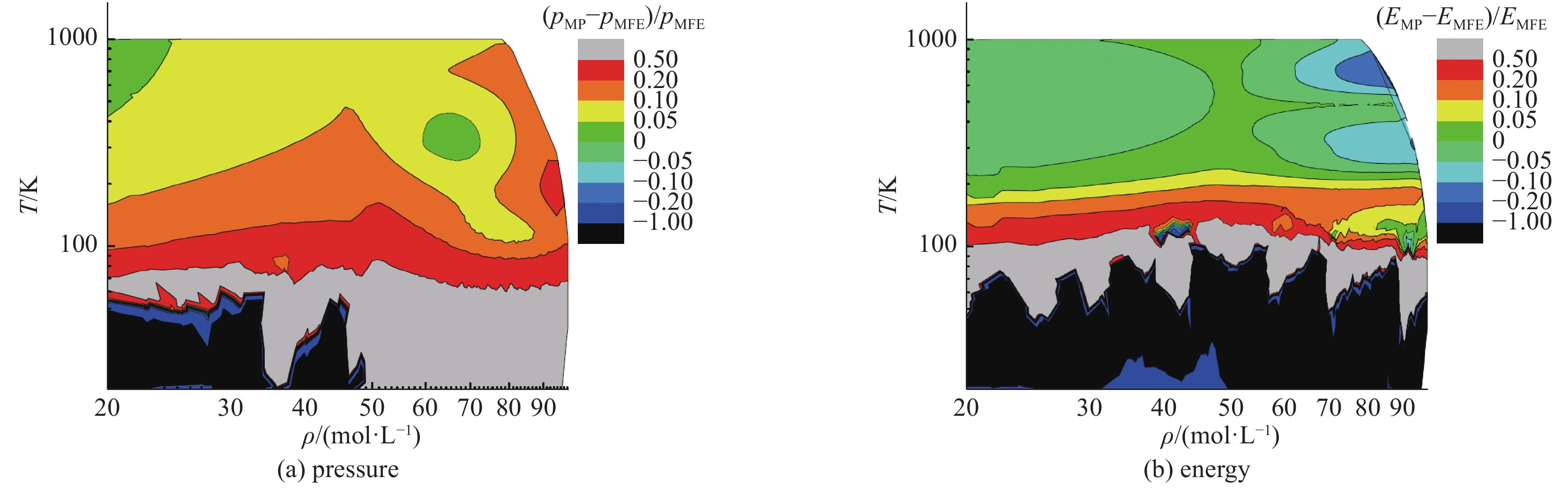
图 7 WEOS氢数据库与DFT数据[23]的压强和能量相对偏差
Figure 7. Relative differences of equation of state for hydrogen between DFT and WEOS
图 8 氢WEOS数据库与H-REOS3数据库的压强和能量相对偏差
Figure 8. Relative differences of equation of state for hydrogen between REOS and WEOS.
表 1 OMEGA装置预压缩氢实验样品初态及不同物态方程计算结果
Table 1. Initioal state of pre-compression hydrogen：experimental data on OMEGA and results from different models
shot ρ0/（104 g·cm−3） p0/GPa p0WEOS/GPa p0MP/GPa p0FP/GPa p0REOS/GPa 34834 881±36 0.31 0.30785 0.30786 0.28581 0.2794 34835 754±46 0.22 0.21811 0.21811 0.26239 0.2003 36174 1216±19 0.70 0.70278 0.70268 0.54969 0.6477 36176 1241±18 0.74 0.74458 0.74452 0.58391 0.6872 38326 576±68 0.13 0.12936 0.12936 0.26881 0.1210 38991 1204±19 0.68 0.68338 0.68334 0.53405 0.6294 38997 644±59 0.16 0.15893 0.15893 0.26314 0.1476 39000 1575±10 1.48 1.51504 1.56795 1.27030 1.4040 41451 1561±11 1.44 1.47493 1.52092 1.23248 1.3660 41458 644±59 0.16 0.15893 0.15893 0.26314 0.1476 43297 869±37 0.30 0.29825 0.29825 0.28216 0.2710 43298 1535±11 1.37 1.40234 1.43708 1.16443 1.2970 47716 644±59 0.16 0.15893 0.15893 0.26314 0.1476 47719 829±40 0.27 0.26800 0.26800 0.27231 0.2444 52250 893±35 0.32 0.31772 0.31772 0.28980 0.2881 53835 869±37 0.30 0.29825 0.29825 0.28216 0.2710 53838 644±59 0.16 0.15893 0.15893 0.26314 0.1476 55003 869±37 0.30 0.29825 0.29825 0.28216 0.2710 56366 1571±10 1.47 1.50350 1.55438 1.25941 1.3930 50377 869±37 0.30 0.29825 0.29825 0.28216 0.2710 53471 644±59 0.16 0.15893 0.15893 0.26314 0.1476 53472 869±37 0.30 0.29825 0.29825 0.28216 0.2710 53478 905±34 0.33 0.32785 0.32785 0.29413 0.2970 
下载: 导出CSV
-
[1] McMahon J M, Morales M A, Pierleoni C, et al. The properties of hydrogen and helium under extreme conditions[J]. Rev Mod Phys, 2012, 84: 1607. doi: 10.1103/RevModPhys.84.1607 [2] Azadi S, Foulkesw M C. Fate of density functional theory in the study of high-pressure solid hydrogen[J]. Phys Rev B, 2013, 88: 014115. doi: 10.1103/PhysRevB.88.014115 [3] Knudson M D, Desjarlais M P. High-precision shock wave measurements of deuterium: evaluation of exchange correlation functions at the molecular-to-atomic transition[J]. Phys Rev Lett, 2017, 118: 035501. doi: 10.1103/PhysRevLett.118.035501 [4] Stevenson D J. Interiors of the giant planets[J]. Annu Rev Earth Planet Sci, 1982, 10: 257-295. doi: 10.1146/annurev.ea.10.050182.001353 [5] Hubbard W B, Militzer B. A preliminary Jupiter model[J]. The Astrophysical J, 2016, 820(1): 80. doi: 10.3847/0004-637X/820/1/80 [6] Wahl S M, Hubbard W B, Militzer B, et al. Comparing Jupiter interior structure models to Juno gravity measurements and the role of a dilute core[J]. Geophys Res Lett, 2017, 44(10): 4649. doi: 10.1002/2017GL073160 [7] Da Silva L B, Celliers P, Collins G W, et al. Absolute equation of state measurements on shocked liquid deuterium up to 200 GPa (2 Mbar)[J]. Phys Rev Lett, 1997, 78: 483-486. doi: 10.1103/PhysRevLett.78.483 [8] Meezan N B, Edwards M J, Hurricane O A, et al. Indirect drive ignition at the National Ignition Facility[J]. Plasma Phys Controlled Fusion, 2017, 59: 014021. doi: 10.1088/0741-3335/59/1/014021 [9] Lindl J D, Amendt P, Berger R L, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility[J]. Phys Plasmas, 2004, 11: 339. doi: 10.1063/1.1578638 [10] Noh J, Fulgueras A M, Sebastian L J, et al. Estimation of thermodynamic properties of hydrogen isotopes and modeling of hydrogen isotope systems using Aspen Plus simulator[J]. Journal of Industrial and Engineering Chemistry, 2017, 46: 1-8. doi: 10.1016/j.jiec.2016.07.053 [11] Hu S, Militzer B, Goncharov V, et al. First-principles equation-of-state table of deuterium for inertial confinement fusion applications[J]. Phys Rev B, 2011, 84: 224109. doi: 10.1103/PhysRevB.84.224109 [12] Liu H F, Song H F, Zhang Q L, et al. Validation for equation of state in wide regime: Copper as prototype[J]. Matter and Radiation at Extremes, 2016, 1: 123-131. doi: 10.1016/j.mre.2016.03.002 [13] Becker A, Lorenzen W, Fortney J J, et al. Ab initio equations of state for hydrogen (H-REOS.3) and helium (He-REOS.3) and their implications for the interior of brown dwarfs[J]. Astrophys J Supp Ser, 2014, 215: 21. doi: 10.1088/0067-0049/215/2/21 [14] Morales M A, Benedict L X, Clark D S, et al. Ab initio calculations of the equation of state of hydrogen in a regime relevant for inertial fusion applications[J]. High Energy Density Phys, 2012, 8: 5-12. doi: 10.1016/j.hedp.2011.09.002 [15] More R M, Warren K H, Young D A, et al. A new quotidian equation of state (QEOS) for hot dense matter[J]. Phys Fluids, 1988, 31: 3059. doi: 10.1063/1.866963 [16] Kerley G I. Equations of state for hydrogen and deuterium[R]. SAND2003-3613, 2003. [17] Kerley G I. A theoretical equation of state for deuterium[R]. LA-4776, 1972. [18] Nettelmann N, Becker A, Holst B, et al. Jupiter models with improved ab initio hydrogen equation of state (H-REOS.2)[J]. Astrophys J, 2012, 750: 52. doi: 10.1088/0004-637X/750/1/52 [19] Saumon D. A new tabular EOS for hydrogen isotopes[J] AIP Conf Proc,2007, 955: 101. [20] Saumon D. Update to SCvH95 using statistical mechanics to produce a fluid hydrogen free energy[R]. LA-UR-13-20032, 2012. [21] Caillabet L, Mazevet S, Loubeyre P. Multiphase equation of state of hydrogen from ab initio calculations in the range 0.2 to 5 g/cc up to 10 eV[J]. Phys Rev B, 2011, 83: 094101. doi: 10.1103/PhysRevB.83.094101 [22] Trunin R F, Urlin V D, Medvedev A B. Dynamic compression of hydrogen isotopes at megabar pressures[J]. Physics –Uspekhi, 2010, 53(6): 577-593. doi: 10.3367/UFNe.0180.201006d.0605 [23] Wang C, Zhang P. Wide range equation of state for fluid hydrogen from density function theory[J]. Phys Plasmas, 2013, 20: 092703. doi: 10.1063/1.4821839 [24] Correa A A, Benedict L X, Young D A, et al. First-principles multiphase equation of state of carbon under extreme conditions[J]. Phys Rev B, 2008, 78: 024101. [25] Hu S X, Goncharov V N, Boehly T R, et al. Impact of first-principles properties of deuterium-tritium on inertial confinement fusion target designs[J]. Phys Plasmas, 2015, 22: 056304. doi: 10.1063/1.4917477 [26] Nellis W J, Mitchell A C, van Thiel M, et al. Equation-of-state data for molecular hydrogen and deuterium at shock pressures in the range 2-76 GPa (20-760 kbar)[J]. J Chem Phys, 1983, 79: 1480. doi: 10.1063/1.445938 [27] Knudson M D, Hanson D H, Bailey J E, et al. Equation of state measurements in liquid deuterium to 70 GPa[J]. Phys Rev Lett, 2001, 87: 225501. doi: 10.1103/PhysRevLett.87.225501 [28] Boriskov G V, Bykov A I, Il'kaev R I, et al. Shock compression of liquid deuterium up to 109 GPa[J]. Phys Rev B, 2005, 71: 092104. doi: 10.1103/PhysRevB.71.092104 [29] Hicks D G, Boehly T R, Celliers P M, et al. Laser-driven single shock compression of fluid deuterium from 45 to 220 GPa[J]. Phys Rev B, 2009, 79: 014112. doi: 10.1103/PhysRevB.79.014112 [30] Loubeyre P, Brygoo S, Eggert J H, et al. Extended data set for the equation of state of warm dense hydrogen isotopes[J]. Phys Rev B, 2012, 86: 144115. doi: 10.1103/PhysRevB.86.144115 [31] Dick R D, Kerley G I. Shock compression data for liquids Ⅱ–Condensed hydrogen and deuterium[J]. J Chem Phys, 1980, 73: 5264. doi: 10.1063/1.439955 [32] 刘海风, 张弓木, 张其黎, 等. 氢氘物态方程研究进展[J]. 高压物理学报, 2018, 32:050101. (Liu Haifeng, Zhang Gongmu, Zhang Qili, et al. Progress on equation of state of hydrogen and deuterium[J]. Chinese Journal of High Pressure Physics, 2018, 32: 050101 [33] Fernandez-Pañella A, Millot M, Fratandon D E, et al. Shock compression of liquid deuterium up to 1 TPa[J]. Phys Rev Lett, 2019, 122: 255702. doi: 10.1103/PhysRevLett.122.255702 [34] Fratanduono D E, Millot M, Fernandez Pañella A, et al. Measurement of the sound speed in dense fluid deuterium along the cryogenic liquid Hugoniot[J]. Phys Plasmas, 2019, 26: 012710. doi: 10.1063/1.5053994 [35] 李琼, 刘海风, 张弓木, 等. 模拟退火算法在化学自由能模型中的应用[J]. 计算物理, 2019, 36(3):259-264. (Li Qiong, Liu Haifeng, Zhang Gongmu, et al. Application of simulated annealing method in chemical free energy model[J]. Chinese Journal of Computational Physics, 2019, 36(3): 259-264 [36] 李琼, 刘海风, 张弓木. 基于化学自由能模型的氢的状态方程与压致离化研究[R]. GFI-0607-04, 2017. Li Qiong, Liu Haifeng, Zhang Gongmu. The equation of state and pressure dissociation of hydrogen from the chemical free energy model[R]. GFI-0607-04, 2017 [37] 刘海风, 张广才. 液氘的分子动力学研究[R]. GF02-035-01, 2002. Liu Haifeng, Zhang Guangcai. The simulation of molecular dynamic for liquid deuterium[R]. GF02-035-01, 2002 [38] 张其黎, 张弓木, 刘海风. 氢、氘状态方程第一原理分子动力学方法研究[R]. GFI-0412-01, 2012. Zhang Qili, Zhang Gongmu, Liu Haifeng. The first principle molecular dynamics study the equation of states for hydrogen and deuterium[R]. GFI-0412-01, 2012 [39] 张其黎, 刘海风, 张弓木. 氘氦混合物状态方程研究[R]. GFI-0412-02, 2012. Zhang Qili, Liu Haifeng, Zhang Gongmu. The study of the equation of states for deuterium and helium mixture. GFI-0412-02, 2012 [40] 张其黎, 刘海风, 李琼, 等. 氢状态方程的路径积分蒙特卡洛研究[J]. 计算物理, 2019, 36(4):379-385. (Zhang QiLi, Liu Haifeng, Li Qiong, et al. Equations of state of hydrogen studied by path integral monte carlo method[J]. Chinese Journal of computational physicse, 2019, 36(4): 379-385 [41] 张其黎. 氢状态方程的理论模型研究[R]. GFI-0611-04, 2018. Zhang Qili. The study of theory models of the equation of states for hydrogen[R], GFI-0611-04, 2018 [42] 张其黎, 马桂存, 刘海风. 液氘的QEOS状态方程研究[R]. GFI-0089-01, 2009. Zhang Qili, Ma Guicun, Liu Haifeng, The quotidian equation of state (QEOS) for liquid deuterium[R]. GFI-0089-01, 2009 [43] Span R, Lemmon E W, Jacobsen R T, et al. A reference equation of state for the thermodynamic properties of nitrogen for temperatures from 63.151 to 1000 K and pressures to 2200 MPa[J]. J Phys Chem Ref Data, 2000, 29: 1361. doi: 10.1063/1.1349047 [44] Leachman J W, Jacobsen R T, Penoncello S G, et al. Fundamental equations of state for parahydrogen, normal hydrogen, and orthohydrogen[J]. J Phys Chem Ref Data, 2006, 38(3): 721-748. [45] Richardson A, Leachman J W, Lemmon E W. Fundamental equation of state for deuterium[J]. J Phys Chem Ref Data, 2013, 43(1): 013103. [46] Richardson I A, Leachman J W, Lemmon E W. Erratum: ‘‘Fundamental equation of state for deuterium’’[J]. J Phys Chem Ref Data, 2018, 47: 049901. doi: 10.1063/1.5016519 [47] 耿华运, 孙毅. 氢的高压奇异结构与金属化[J]. 高压物理学报, 2018, 32:020101. (Geng Huayun, Sun Yi. On the novel structure and metallization of hydrogen under high pressure[J]. Chinese Journal of High Pressure Physics, 2018, 32: 020101 [48] Duffy T S, Vos W L, Zha C S, et al. Sound velocities in dense hydrogen and the interior of Jupiter[J]. Science, 1994, 263: 1590. doi: 10.1126/science.263.5153.1590 [49] Hemley R J, Mao H K. Equation of state of solid hrdrogen and deuterium from single-crystal X-ray diffraction to 26.5 GPa[J]. Phys Rev B, 1990, 42: 106458. [50] Loubeyre P, LeToullec R, Häusermann D, et al. X-ray diffraction and equation of state of hydrogen at megabar pressures[J]. Nature, 1996, 383: 702. doi: 10.1038/383702a0 [51] Hemley R J, Mao H K, Goncharov A F, et al. Synchrotron infrared spectroscopy to 0.15 eV of H2 and D2 at megabar pressures[J]. Phys Rev Lett, 1996, 76: 1667. doi: 10.1103/PhysRevLett.76.1667 [52] Rillo G, Morales M A, Ceperley D M, et al. Coupled electron-ion Monte Carlo simulation of hydrogen molecular crystals[J]. Journal of Chemical Physics, 2018, 148: 102314. doi: 10.1063/1.5001387 [53] Geng H Y, Song H X, Li J F, et al. High-pressure behavior of dense hydrogen up to 3.5 TPa from density functional theory calculations[J]. J Appl Phys, 2012, 111: 063510. doi: 10.1063/1.3694793 [54] Van Thiel M, Alder B J. Shock compression of liquid hydrogen[J]. Molecular Physics, 1966, 10(5): 427-435. doi: 10.1080/00268976600100551 [55] Brygoo S, Millot M, Loubeyre P, et al. Analysis of laser shock experiments on precompressed samples using a quartz reference and application to warm dense hydrogen and helium[J]. Journal of Applied Physics, 2015, 118: 195901. doi: 10.1063/1.4935295 [56] Knudson M D, Hanson D L, Bailey J E, et al. Principal Hugoniot, reverberating wave, and mechanical reshock measurements of liquid deuterium to 400 GPa using plate impact techniques[J]. Phys Rev B, 2004, 69: 144209. doi: 10.1103/PhysRevB.69.144209 [57] 贾果, 黄秀光, 谢志勇, 等. 液氘状态方程实验数据测量[J]. 物理学报, 2015, 64:166401. (Jia Guo, Huang Xiuguang, Xie Zhiyong, et al. Experimental measurement of liquid deuterium equation of state data[J]. Acta Physica Sinica, 2015, 64: 166401 doi: 10.7498/aps.64.166401 [58] Militzer B, Ceperley D M. Path integral Monte Carlo simulation of the low-density hydrogen plasma[J]. Phys Rev E, 1996, 63: 066404. [59] Collins L A, Bickham S R, Kress J D. Dynamical and optical properties of warm dense hydrogen[J]. Phys Rev B, 2001, 63: 184110. doi: 10.1103/PhysRevB.63.184110 [60] Morales M A, Pierleoni C , Ceperley D M. Equation of state of metallic hydrogen from coupled electron-ion Monte Carlo simulations[J]. Phys Rev E, 2010, 81: 021202. [61] Pierleoni C, Ceperley D M, Holzmann M. Coupled electron-ion Monte Carlo calculations of dense metallic hydrogen[J]. Phys Rev Lett, 2004, 93: 146402. doi: 10.1103/PhysRevLett.93.146402 [62] Filinov V S, Bonitz M, Ebeling W, et al. Thermodynamics of hot dense H-plasmas: path integral Monte Carlo simulations and analytical approximations[J]. Plasma Phys Control Fusion, 2001, 43: 743-759. doi: 10.1088/0741-3335/43/6/301 [63] Sano T, Ozaki N, Sakaiya T, et al. Laser-shock compression and Hugoniot measurements of liquid hydrogen to 55 GPa[J]. Phys Rev B, 2011, 83: 054117. doi: 10.1103/PhysRevB.83.054117 [64] Holmes N C, Ross M, Nellis W J. Temperature measurements and dissociation of shock-compressed liquid deuterium and hydrogen[J]. Phys Rev B, 1995, 52: 15835. doi: 10.1103/PhysRevB.52.15835 [65] Brody E B, Shimizu H, Mao H K, et al. Acoustic velocity and refractive index of fluid hydrogen and deuterium at high pressures[J]. J Appl Phys, 1981, 52: 3583. doi: 10.1063/1.329141 [66] Shimizu H, Brody E M, Mao H K, et al. Brillouin measurements of solid n-H2 and n-D2 to 200 kbar at room temperature[J]. Phys Rev Lett, 1981, 47: 128. doi: 10.1103/PhysRevLett.47.128 [67] 何以广, 王钊, 汤秀章. 低Z流体的单次冲击波压缩极限[J]. 强激光与粒子束, 2010, 22(10):2432-2436. (He Yiguang, Wang Zhao, Tang Xiuzhang. Single-shock compression limit of low-Z fluids[J]. High Power Laser and Particle Beams, 2010, 22(10): 2432-2436 doi: 10.3788/HPLPB20102210.2432 [68] 王聪, 贺贤土, 张平. 氢及其同位素宽区状态方程的核量子效应[J]. 强激光与粒子束, 2015, 27:032008. (Wang Cong, He Xiantu, Zhang Ping. Quantum nuclear effects in the wide range equations of states for hydrogen and its isotopes[J]. High Power Laser and Particle Beams, 2015, 27: 032008 doi: 10.11884/HPLPB201527.032008 [69] Gregoryanz E, Ji Cheng, Dalladay-Simpson P, et al. Everything you always wanted to know about metallic hydrogen but were afraid to ask[J]. Matter and Radiation at Extremes, 2020, 5: 038101. doi: 10.1063/5.0002104 [70] Ji Cheng, Li Bing, Liu Wenjun, et al. Crystallography of low Z material at ultrahigh pressure: Case study on solid hydrogen[J]. Matter and Radiation at Extremes, 2020, 5: 038401. doi: 10.1063/5.0003288 [71] Zeldovich Y B, Raizer Y R. Physics of shock waves and high temperature hydrodynamic phenomena[M]. Cambridge: Cambridge University Press, 1966. [72] Nellis W J. Shock compression of deuterium near 100 GPa pressures[J]. Phys Rev Lett, 2002, 89: 165502. doi: 10.1103/PhysRevLett.89.165502 -
点击查看大图
图(17) / 表 (1)
计量
- 文章访问数: 163
- HTML全文浏览量: 92
- PDF下载量: 24
- 被引次数: 0
