Development and application of the theoretical models for stimulated scattering processes
-
摘要: 在激光间接驱动的惯性约束聚变(ICF)中,高强度激光与低密度等离子体发生相互作用,会激发两种受激散射过程:受激布里渊散射和受激拉曼散射。它们会损失激光能量、破坏辐射场对称性、产生超热电子,从而危害聚变点火过程。因此,理解受激散射的物理过程并找到抑制其发展的有效方法,是ICF研究中重点关注的问题。介绍了中国激光聚变研究团队为研究受激散射过程而发展的多个理论模型,以及这些模型在实验数据分析中的具体应用。这些理论模型与实验研究一起,为提升受激散射过程的物理理解发挥了重要作用。Abstract: In laser indirect-drive inertial confinement fusion (ICF), the interaction of high-intensity laser and under-dense plasmas will excite two stimulated scattering processes: stimulated Brillouin scattering (SBS) and stimulated Raman scattering (SRS). These processes are detrimental to ignition since they consume laser energy, break symmetry of the X-ray radiation, and produce energetic electrons. Therefore, comprehending the basic physics of the stimulated scattering processes and hence finding effective approaches to suppress them are great concerns in ICF research. This article introduces several theoretical models developed by Chinese researchers for studying stimulated scattering processes, as well as their applications in analysis of experimental data. These theoretical models, together with the experiments, play important roles in improving the physical understanding of the stimulated scattering processes.
-
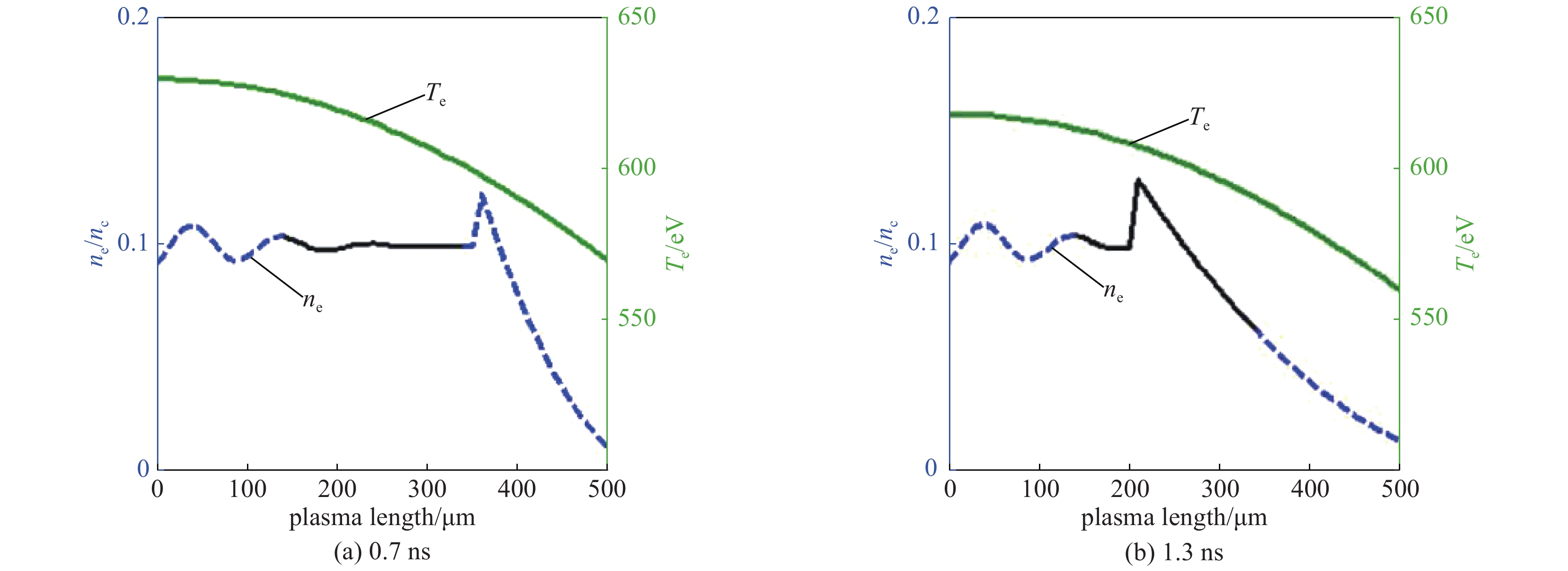
图 1 气袋靶实验中,电子密度和温度在不同时刻的空间分布(图片来自于参考文献[45])
Figure 1. Electron density and temperature profiles in a gasbag target at different times
图 2 实验诊断的SRS条纹谱和计算得到的SRS增益因子(图片来自于参考文献[45])
Figure 2. Experimentally measured stimulated Brillouin scattering (SRS) streak spectrum and calculated gain factor of stimulated Raman scattering (SRS)
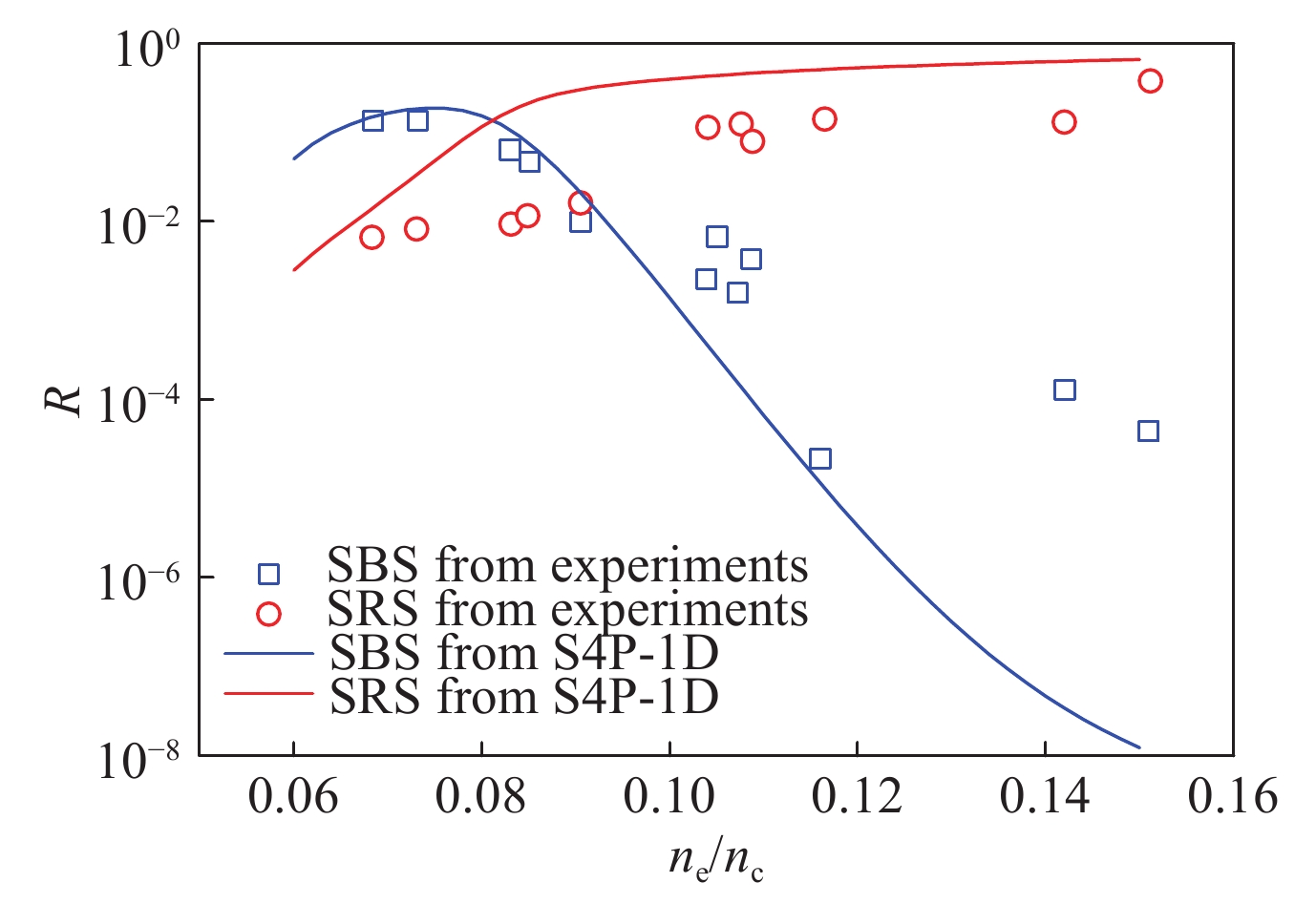
图 3 气袋靶实验中SBS和SRS散射光份额随电子密度的变化规律(图片来自于参考文献[56])
Figure 3. Reflectivities of SBS and SRS as functions of electron density from gasbag experiments
图 4 不同电子密度下的SBS和SRS线性增益因子(图片来自于参考文献[56])
Figure 4. Linear gains of SBS and SRS at different electron densities
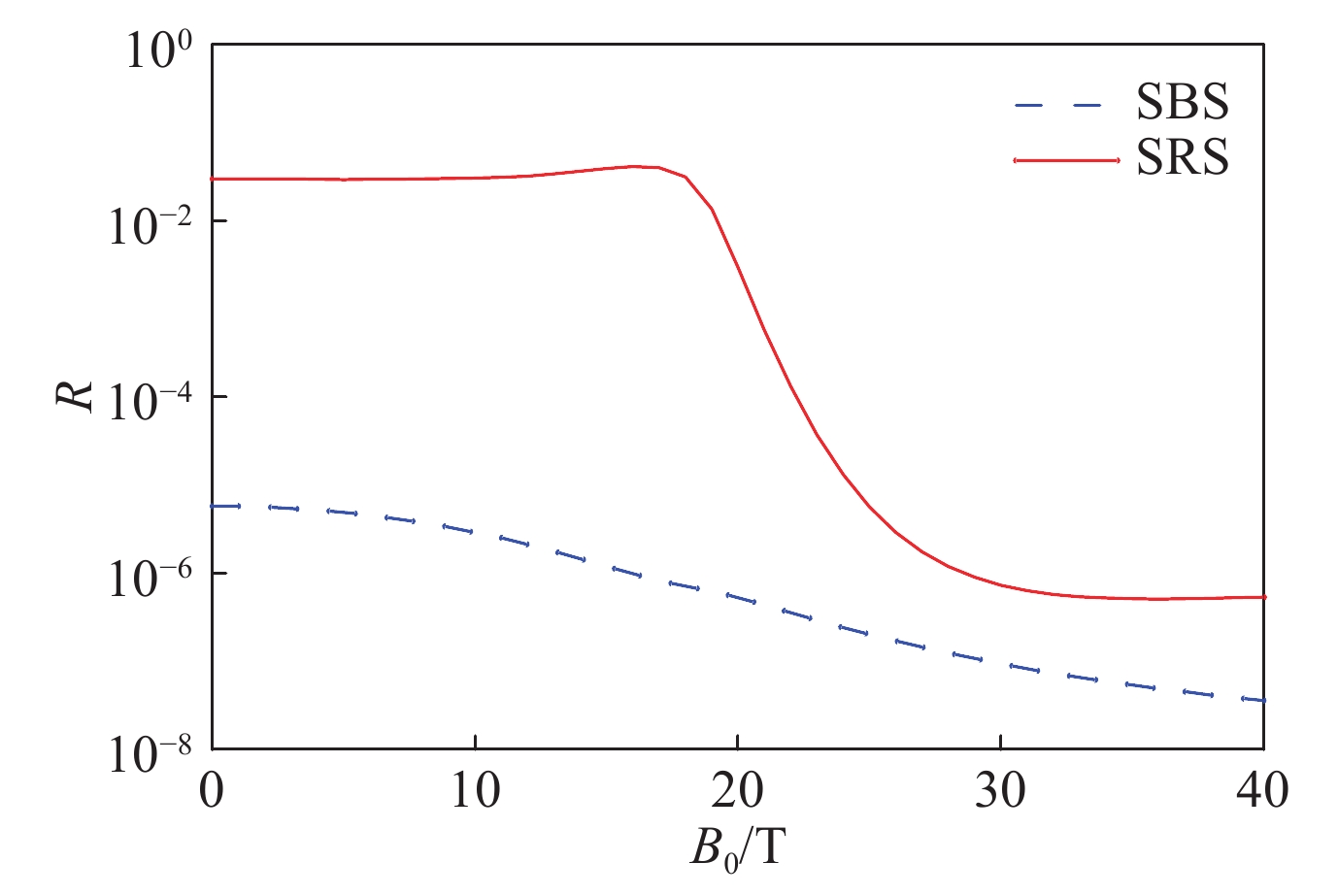
图 5 SBS和SRS散射光份额随外加磁场强度的变化曲线(图片来自于参考文献[57])
Figure 5. Reflectivities of SBS and SRS as functions of the intensity of external magnetic field
图 6 SBS光谱(图片来自于参考文献[48])
Figure 6. SBS spectra
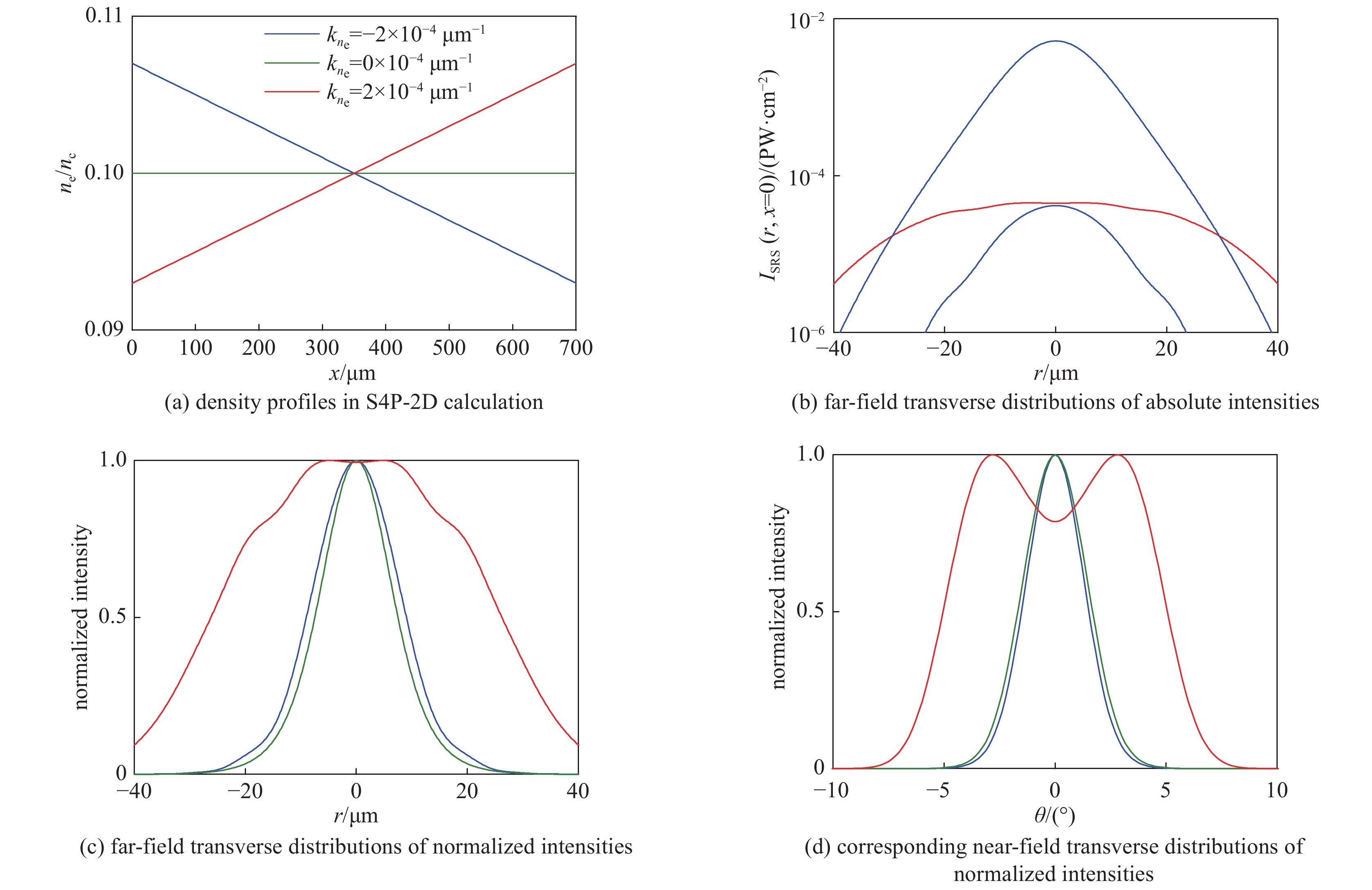
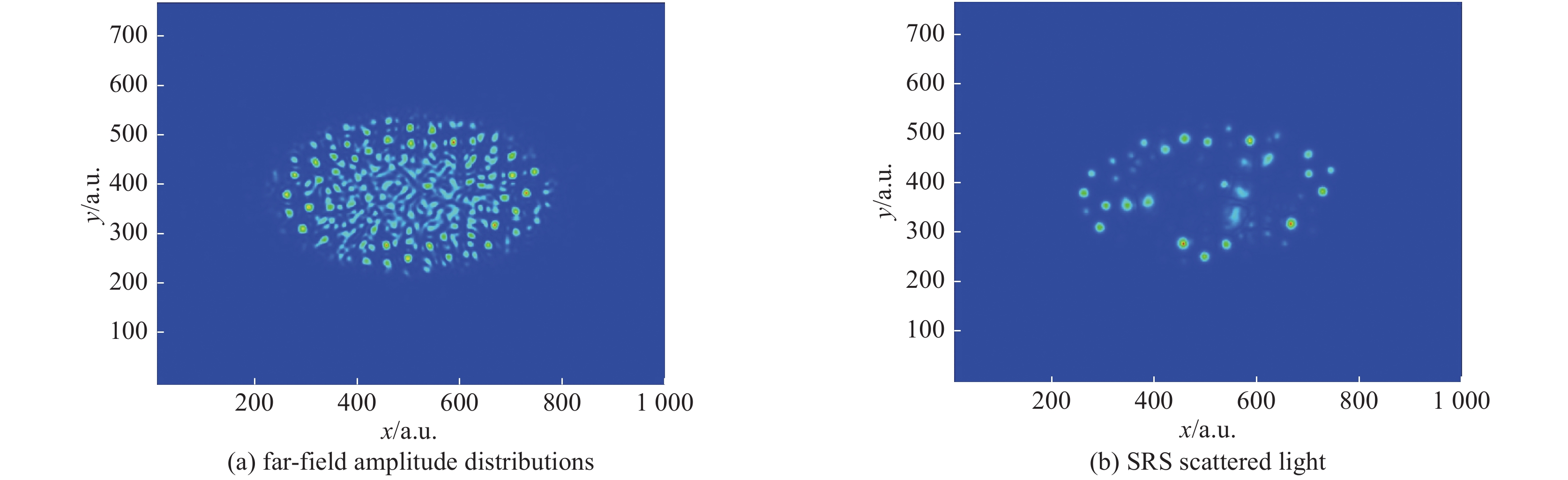
图 8 使用CPP的激光及其SRS散射光的振幅远场分布(图片来自于参考文献[54])
Figure 8. Far-field amplitude distributions of an incident laser with CPP and its SRS scattered light
-
[1] Lindl J. Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain[J]. Physics of Plasmas, 1995, 2(11): 3933-4024. doi: 10.1063/1.871025 [2] Lindl J, Amendt P, Berger R L, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility[J]. Physics of Plasmas, 2004, 11(2): 339-491. doi: 10.1063/1.1578638 [3] Kruer W L. The physics of laser plasma interactions[M]. Redwood: Addison-Wesley, 1988. [4] Tang C L. Saturation and spectral characteristics of the Stokes emission in the stimulated Brillouin process[J]. Journal of Applied Physics, 1966, 37(8): 2945-2955. doi: 10.1063/1.1703144 [5] Labaune C, Baldis H A, Bauer B S. Time-resolved measurements of secondary Langmuir waves produced by the Langmuir decay instability in a laser-produced plasma[J]. Physics of Plasmas, 1998, 5(1): 234-242. doi: 10.1063/1.872692 [6] Depierreux S, Labaune C, Fuchs J, et al. Langmuir decay instability cascade in laser-plasma experiments[J]. Physical Review Letters, 2002, 89: 045001. doi: 10.1103/PhysRevLett.89.045001 [7] Bandulet H C, Labaune C, Lewis K, et al. Thomson-scattering study of the subharmonic decay of ion-acoustic waves driven by the Brillouin instability[J]. Physical Review Letters, 2004, 93: 035002. doi: 10.1103/PhysRevLett.93.035002 [8] Niemann C, Glenzer S H, Knight J, et al. Observation of the parametric two-ion decay instability with Thomson scattering[J]. Physical Review Letters, 2004, 93: 045004. doi: 10.1103/PhysRevLett.93.045004 [9] Morales G J, O’neil T M. Nonlinear frequency-shift of an electron-plasma wave[J]. Physical Review Letters, 1972, 28(7): 417-420. doi: 10.1103/PhysRevLett.28.417 [10] Giacone R E, Vu H X. Nonlinear kinetic simulations of stimulated Brillouin scattering[J]. Physics of Plasmas, 1998, 5(5): 1455-1460. doi: 10.1063/1.872803 [11] Froula D H, Divol L, Glenzer S H. Measurements of nonlinear growth of ion-acoustic waves in two-ion-species plasmas with Thomson scattering[J]. Physical Review Letters, 2002, 88: 105003. doi: 10.1103/PhysRevLett.88.105003 [12] Divol L, Berger R L, Cohen B I, et al. Modeling the nonlinear saturation of stimulated Brillouin backscatter in laser heated plasmas[J]. Physics of Plasmas, 2003, 10(5): 1822-1828. doi: 10.1063/1.1557055 [13] 李志超. 大尺度激光等离子体相互作用的实验研究[D]. 合肥: 中国科学技术大学, 2011: 12-14.Li Zhichao. Experimental research on large-scale laser-plasma interactions[D]. Hefei: University of Science and Technology of China, 2011: 12-14 [14] 龚韬. 激光间接驱动惯性约束聚变中受激散射过程的理论和实验研究[D]. 合肥: 中国科学技术大学, 2015: 52-58.Gong Tao. Theoretical and experimental study on the stimulated scattering in laser indirect-drive inertial confinement fusion[D]. Hefei: University of Science and Technology of China, 2015: 52-58 [15] Meezan N B, Berger R L, Divol L, et al. Role of hydrodynamics simulations in laser-plasma interaction predictive capability[J]. Physics of Plasmas, 2007, 14: 056304. doi: 10.1063/1.2710782 [16] Froula D H, Divol L, Meezan N B, et al. Ideal laser-beam propagation through high-temperature ignition hohlraum plasmas[J]. Physical Review Letters, 2007, 98: 085001. doi: 10.1103/PhysRevLett.98.085001 [17] Froula D H, Divol L, Meezan N B, et al. Laser beam propagation through inertial confinement fusion hohlraum plasmas[J]. Physics of Plasmas, 2007, 14: 055705. doi: 10.1063/1.2515054 [18] Hinkel D E, Callahan D A, Langdon A B, et al. Analyses of laser-plasma interactions in National Ignition Facility ignition targets[J]. Physics of Plasmas, 2008, 15: 056314. doi: 10.1063/1.2901127 [19] Neumayer P, Berger R L, Callahan D, et al. Energetics of multiple-ion species hohlraum plasmas[J]. Physics of Plasmas, 2008, 15: 056307. doi: 10.1063/1.2890126 [20] Hinkel D E, Rosen M D, Williams E A, et al. Stimulated Raman scatter analyses of experiments conducted at the National Ignition Facility[J]. Physics of Plasmas, 2011, 18: 056312. doi: 10.1063/1.3577836 [21] Neumayer P, Berger R L, Divol L, et al. Suppression of stimulated Brillouin scattering by increased Landau damping in multiple-ion-species hohlraum plasmas[J]. Physical Review Letters, 2008, 100: 105001. doi: 10.1103/PhysRevLett.100.105001 [22] Froula D H, Divol L, London R A, et al. Pushing the limits of plasma length in inertial-fusion laser-plasma interaction experiments[J]. Physical Review Letters, 2008, 100: 015002. doi: 10.1103/PhysRevLett.100.015002 [23] Rosenbluth M N. Parametric instabilities in inhomogeneous media[J]. Physical Review Letters, 1972, 29(9): 565-567. doi: 10.1103/PhysRevLett.29.565 [24] Liu C S, Rosenbluth M N, White R B. Raman and Brillouin-scattering of electromagnetic-waves in inhomogeneous plasmas[J]. Physics of Fluids, 1974, 17(6): 1211-1219. doi: 10.1063/1.1694867 [25] Ramani A, Max C E. Stimulated Brillouin-scattering in an inhomogeneous-plasma with broad-bandwidth thermal noise[J]. Physics of Fluids, 1983, 26(4): 1079-1102. doi: 10.1063/1.864220 [26] Berger R L, Williams E A, Simon A. Effect of plasma noise spectrum on stimulated scattering in inhomogeneous-plasma[J]. Physics of Fluids B, 1989, 1(2): 414-421. doi: 10.1063/1.859155 [27] Mounaix P, Pesme D, Casanova M. Nonlinear reflectivity of an inhomogeneous plasma in the strongly damped regime[J]. Physical Review E, 1997, 55(4): 4653-4664. doi: 10.1103/PhysRevE.55.4653 [28] Berger R L, Still C H, Williams E A, et al. On the dominant and subdominant behavior of stimulated Raman and Brillouin scattering driven by nonuniform laser beams[J]. Physics of Plasmas, 1998, 5(12): 4337-4356. doi: 10.1063/1.873171 [29] Strozzi D J, Williams E A, Hinkel D E, et al. Ray-based calculations of backscatter in laser fusion targets[J]. Physics of Plasmas, 2008, 15: 102703. doi: 10.1063/1.2992522 [30] Strozzi D J, Bailey D S, Michel P, et al. Interplay of laser-plasma interactions and inertial fusion hydrodynamics[J]. Physical Review Letters, 2017, 118: 025002. doi: 10.1103/PhysRevLett.118.025002 [31] Hall G N, Jones O S, Strozzi D J, et al. The relationship between gas fill density and hohlraum drive performance at the National Ignition Facility[J]. Physics of Plasmas, 2017, 24: 052706. doi: 10.1063/1.4983142 [32] Sodha M S, Sharma R P, Kaushik S C. Interaction of intense laser beams with plasma waves: Stimulated Raman scattering[J]. Journal of Applied Physics, 1976, 47(8): 3518-3523. doi: 10.1063/1.323194 [33] Sodha M S, Umesh G, Sharma R P. Enhanced Brillouin scattering of a Gaussian laser beam from a plasma[J]. Journal of Applied Physics, 1979, 50(7): 4678-4684. doi: 10.1063/1.326577 [34] Sharma R P, Vyas A, Singh R K. Effect of laser beam filamentation on coexisting stimulated Raman and Brillouin scattering[J]. Physics of Plasmas, 2013, 20: 102108. doi: 10.1063/1.4824738 [35] Vyas A, Singh R K, Sharma R P. Combined effect of relativistic and ponderomotive filamentation on coexisting stimulated Raman and Brillouin scattering[J]. Physics of Plasmas, 2014, 21: 112113. doi: 10.1063/1.4902107 [36] Amin M R, Capjack C E, Frycz P, et al. Two-dimensional simulations of stimulated Brillouin-scattering in laser-produced plasmas[J]. Physical Review Letters, 1993, 71(1): 81-84. doi: 10.1103/PhysRevLett.71.81 [37] Amin M R, Capjack C E, Frycz P, et al. Two-dimensional studies of stimulated Brillouin scattering, filamentation, and self-focusing instabilities of laser light in plasmas[J]. Physics of Fluids B, 1993, 5(10): 3748-3764. doi: 10.1063/1.860845 [38] Divol L, Berger R L, Meezan N B, et al. Three-dimensional modeling of stimulated Brillouin scattering in ignition-scale experiments[J]. Physical Review Letters, 2008, 100: 255001. doi: 10.1103/PhysRevLett.100.255001 [39] Divol L, Berger R L, Meezan N B, et al. Three-dimensional modeling of laser-plasma interaction: Benchmarking our predictive modeling tools versus experiments[J]. Physics of Plasmas, 2008, 15: 056313. doi: 10.1063/1.2844361 [40] Berger R L, Suter L J, Divol L, et al. Beyond the gain exponent: Effect of damping, scale length, and speckle length on stimulated scatter[J]. Physical Review E, 2015, 91: 031103. doi: 10.1103/PhysRevE.91.031103 [41] Berger R L, Thomas C A, Baker K L, et al. Stimulated backscatter of laser light from BigFoot hohlraums on the National Ignition Facility[J]. Physics of Plasmas, 2019, 26: 012709. doi: 10.1063/1.5079234 [42] 李志超, 张小丁, 杨冬, 等. 神光Ⅲ原型受激拉曼与受激布里渊散射份额测量[J]. 强激光与粒子束, 2010, 22(8):1891-1895. (Li Zhichao, Zhang Xiaoding, Yang Dong, et al. Energy fraction measurements of stimulated Brillouin scattering and stimulated Raman scattering on Shenguang-III prototype laser facility[J]. High Power Laser and Particle Beams, 2010, 22(8): 1891-1895 doi: 10.3788/HPLPB20102208.1891 [43] Li Zhichao, Zheng Jian, Ding Yongkun, et al. Generation and characterization of millimeter-scale plasmas for the research of laser plasma interactions on Shenguang-III prototype[J]. Chinese Physics B, 2010, 19:125202. [44] LiZhichao, Zheng Jian, Jiang Xiaohua, et al. Methods of generation and detailed characterization of millimeter-scale plasmas using a gasbag target[J]. Chinese Physics Letters, 2011, 28: 125202. doi: 10.1088/0256-307X/28/12/125202 [45] Li Zhichao, Zheng Jian, Jiang Xiaohua, et al. Interaction of 0.53 μm laser pulse with millimeter-scale plasmas generated by gasbag target[J]. Physics of Plasmas, 2012, 19: 062703. doi: 10.1063/1.4729332 [46] Hao Liang, Zhao Yiqing, Yang Dong, et al. Analysis of stimulated Raman backscatter and stimulated Brillouin backscatter in experiments performed on SG-III prototype facility with a spectral analysis code[J]. Physics of Plasmas, 2014, 21: 072705. doi: 10.1063/1.4890019 [47] 杨冬, 李志超, 李三伟, 等. 间接驱动惯性约束聚变中的激光等离子体不稳定性[J]. 中国科学: 物理学 力学 天文学, 2018, 48:065203. (Yang Dong, Li Zhichao, Li Sanwei, et al. Laser plasma instability in indirect-drive inertial confinement fusion[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2018, 48: 065203 [48] Hao Liang, Yang Dong, Li Xin, et al. Investigation on laser plasma instability of the outer ring beams on SGIII laser facility[J]. AIP Advances, 2019, 9: 095201. doi: 10.1063/1.5087936 [49] Gong Tao, Hao Liang, Li Zhichao, et al. Recent research progress of laser plasma interactions in Shenguang laser facilities[J]. Matter and Radiation at Extremes, 2019, 4: 055202. doi: 10.1063/1.5092446 [50] Hao L, Liu Z J, Hu X Y, et al. Competition between the stimulated Raman and Brillouin scattering under the strong damping condition[J]. Laser and Particle Beams, 2013, 31(2): 203-209. doi: 10.1017/S0263034613000074 [51] Hao L, Hu X Y, Zheng C Y, et al. Study of crossed-beam energy transfer process with large crossing angle in three-dimension[J]. Laser and Particle Beams, 2016, 34(2): 270-275. doi: 10.1017/S0263034616000082 [52] Liu Z J, Zhu S P, Cao L H, et al. Enhancement of backward Raman scattering by electron-ion collisions[J]. Physics of Plasmas, 2009, 16: 112703. doi: 10.1063/1.3258839 [53] 刘占军, 郝亮, 项江, 等. 激光聚变中受激布里渊散射的混合模拟研究[J]. 物理学报, 2012, 61:115202. (Liu Zhanjun, Hao Liang, Xiang Jiang, et al. Hybrid simulation of stimulated Brillouin scattering in laser fusions[J]. Acta Physica Sinica, 2012, 61: 115202 doi: 10.7498/aps.61.115202 [54] Liu Z J, Li B, Hu X Y, et al. The light diffraction effect on stimulated Raman scattering[J]. Physics of Plasmas, 2016, 23: 022705. doi: 10.1063/1.4941967 [55] Hu Xiaoyan, Hao Liang, Liu Zhanjun, et al. The development of laser-plasma interaction program LAP3D on thousands of processors[J]. AIP Advances, 2015, 5: 087174. doi: 10.1063/1.4929775 [56] Gong Tao, Li Zhichao, Zhao Bin, et al. Noise sources and competition between stimulated Brillouin and Raman scattering: A one-dimensional steady-state approach[J]. Physics of Plasmas, 2013, 20: 092702. doi: 10.1063/1.4821827 [57] Gong Tao, ZhengJian, Li Zhichao, et al. Mitigating stimulated scattering processes in gas-filled hohlraums via external magnetic fields[J]. Physics of Plasmas, 2015, 22: 092706. doi: 10.1063/1.4931077 [58] Gong Tao, Zheng Jian, Li Zhichao, et al. Frequency mismatch in stimulated scattering processes: An important factor for the transverse distribution of scattered light[J]. Physics of Plasmas, 2016, 23: 063303. doi: 10.1063/1.4954391 [59] Hao L, Yan R, Li J, et al. Nonlinear fluid simulation study of stimulated Raman and Brillouin scatterings in shock ignition[J]. Physics of Plasmas, 2017, 24: 062709. doi: 10.1063/1.4989702 [60] Drake J F, Kaw P K, Lee Y C, et al. Parametric-instabilities of electromagnetic-waves in plasmas[J]. Physics of Fluids, 1974, 17(4): 778-785. doi: 10.1063/1.1694789 [61] Alexandrov A, Bogdankevich L, Rukhadze A. Principles of plasma electrodynamics[M]. Berlin: Springer-Verlag, 1984. [62] Montgomery D S, Afeyan B B, Cobble J A, et al. Evidence of plasma fluctuations and their effect on the growth of stimulated Brillouin and stimulated Raman scattering in laser plasmas[J]. Physics of Plasmas, 1998, 5(5): 1973-1980. doi: 10.1063/1.872868 [63] Tikhonchuk V T, Huller S, Mounaix P. Effect of the speckle self-focusing on the stationary stimulated Brillouin scattering reflectivity from a randomized laser beam in an inhomogeneous plasma[J]. Physics of Plasmas, 1997, 4(12): 4369-4381. doi: 10.1063/1.872599 -




 下载:
下载: