Review of hydrodynamic instabilities in inertial confinement fusion implosions
-
摘要: 激光聚变有望一劳永逸地解决人类的能源问题,因而受到国际社会的普遍重视,一直是国际研究的前沿热点。目前实现激光惯性约束聚变所面临的最大科学障碍(属于内禀困难)是对内爆过程中高能量密度流体力学不稳定性引起的非线性流动的有效控制,对其研究涵盖高能量密度物理、等离子体物理、流体力学、计算科学、强冲击物理和高压原子物理等多个学科,同时还要具备大规模多物理多尺度多介质流动的数值模拟能力和高功率大型激光装置等研究条件。作为新兴研究课题,高能量密度非线性流动问题充满了各种新奇的现象亟待探索。此外,流体力学不稳定性及其引起的湍流混合,还是天体物理现象(如星系碰撞与合并、恒星演化、原始恒星的形成以及超新星爆炸)中的重要过程,涉及天体物理的一些核心研究内容。本文首先综述了高能量密度非线性流动研究的现状和进展,梳理了其中的挑战和机遇。然后介绍了传统中心点火激光聚变内爆过程发生的主要流体力学不稳定性,在大量分解和综合物理研究基础上,凝练出了目前制约美国国家点火装置(NIF)内爆性能的主要流体不稳定性问题。接下来,总结了国外激光聚变流体不稳定性实验物理的研究概况。最后,展示了内爆物理团队近些年在激光聚变内爆流体不稳定性基础性问题方面的主要研究进展。该团队一直从事激光聚变内爆非线性流动研究与控制,以及聚变靶物理研究与设计,注重理论探索和实验研究相结合,近年来在内爆重要流体力学不稳定性问题的解析理论、数值模拟和激光装置实验设计与数据分析等方面取得了一系列重要成果,有力地推动了该研究方向在国内的发展。Abstract: Laser fusion, likely the ultimate solution to the crisis of human energy, is highly valued by the international community and has always been the focus of international research. It turns out that the biggest scientific obstacle of laser fusion is the effective control of the high-energy-density nonlinear flows during implosions. The research of high-energy-density nonlinear flows covers many different fields, such as high-energy-density physics, plasma physics, fluid mechanics, computing science, strong impact physics, and high pressure atomic physics. Meanwhile, the capability of multi-material and multi-scale numerical simulations as well as large laser facility with high output power is also needed. As an emerging research field, it is full of all kinds of novel phenomena to be explored. In addition, hydrodynamic instabilities and the subsequent turbulent mixing in high-energy-density flows, are also important processes in astrophysical phenomena (e.g., galaxy collision and merging, stellar evolution, formation of protostars and supernova explosion) and involve with the core content of astrophysics. This paper reviews, firstly the status and progress, as well as the challenges and opportunities of high-energy-density nonlinear flows research. Secondly, it introduces hydrodynamic instabilities during implosions in central ignition laser fusion, among which, key factors related to the bottleneck of implosion performance of the National Ignition Facility (NIF) in the United States are condensed. Next, it summarizes the development of hydrodynamic instability experiments in laser fusion abroad. Finally, it lists some key achievements on the fundamental issues of hydrodynamic instabilities by the laser fusion implosion physics team in China over the last three years. This team has been engaged in the research and control of nonlinear flows in laser fusion implosions, as well as the research and design of target physics. A lot of improvements have been made in recent years on the theoretical analysis and numerical simulation of outstanding issues for hydrodynamic instabilities in laser fusion implosions, and the design and analysis of experiments on large lasers, which greatly promoted the development of this research direction in China.
-
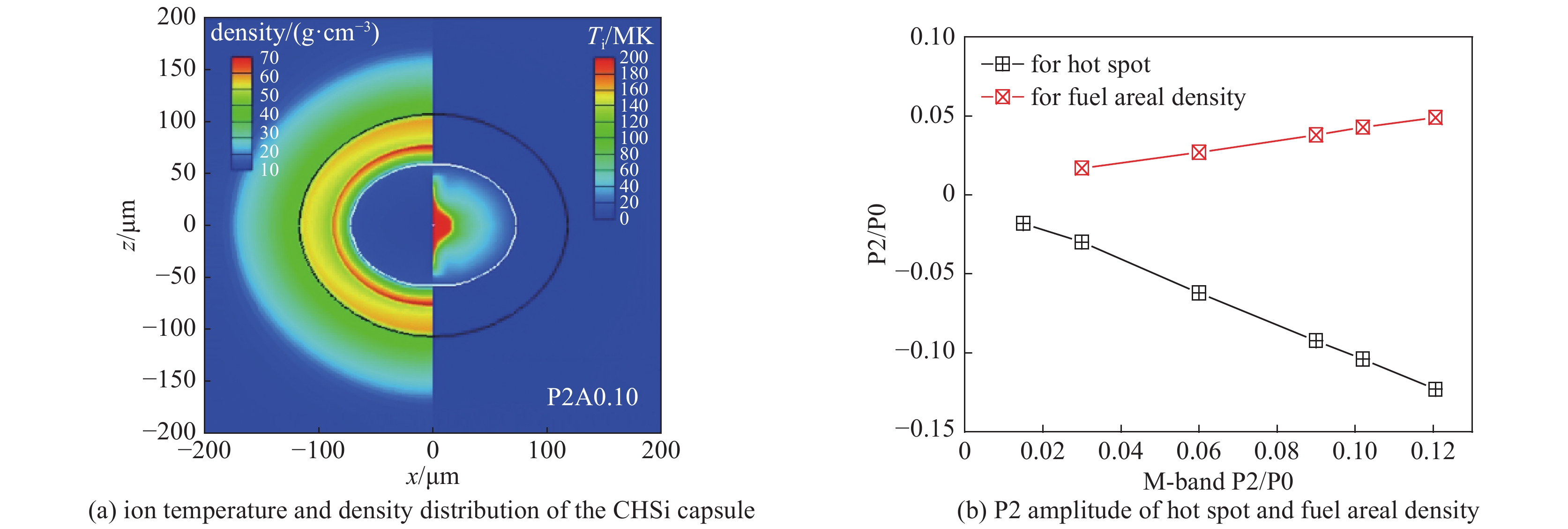
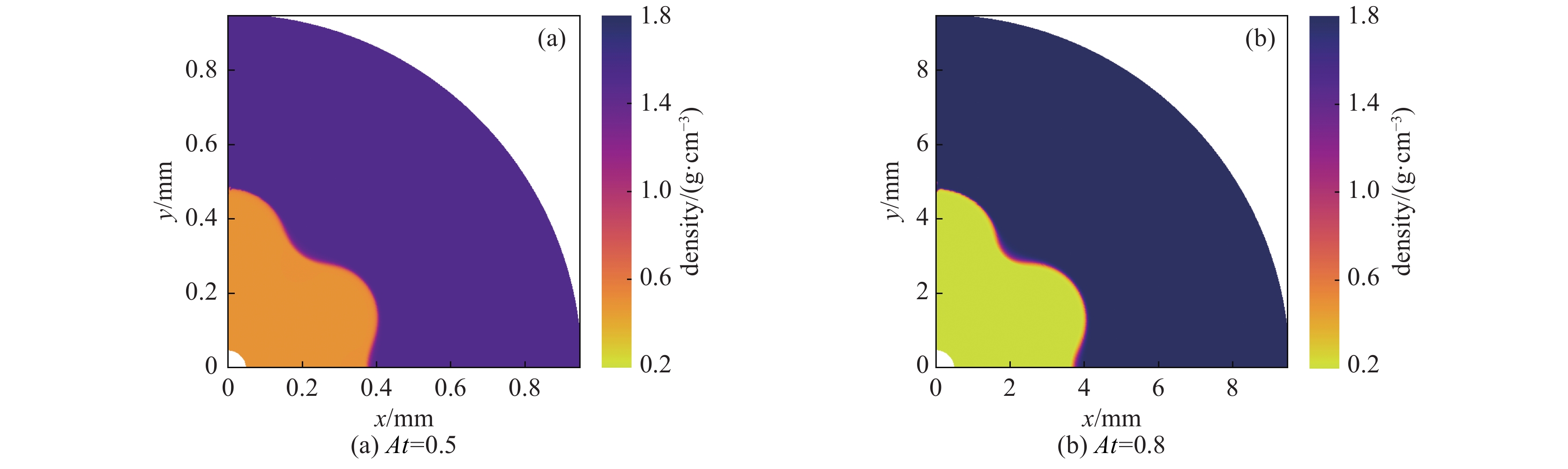
图 12 P2不对称的M带辐射流驱动下靶丸的温度密度分布和靶丸形变随M带P2不对称幅度的变化关系
Figure 12. Ion temperature (right panel) and density (left panel) distribution of the CHSi capsule at the time of peak implosion velocity driven by X-ray drive in figure 11(b) but with P2 asymmetric gold M-band flux
图 13 模拟得到的靶丸核性能(中子产额与一维模拟结果之比,YO1D)随辐射源中M带P2不对称性幅度的变化关系, 黑线对应谱积分的总辐射流对称的情况,红线对应低能段(<1.8 keV)辐射流保持对称的情况,黑色方块和红色菱形分别代表两种情况下YOC降为一半时所对应的悬崖位置
Figure 13. Simulated capsule performance (yield over 1D performance or clean,YO1D) varying with the gold M-band flux asymmetry applied upon the initial capsule surface. The black line corresponds to the situation where total flux is kept symmetric,while the red line corresponds to the other situation where only soft X-ray (<1.8 keV) of the drive is kept symmetric
图 14 两个靶丸壳层飞至相同位置时的温度和金M带辐射流的径向分布;掺Ge靶(蓝线)、掺Si靶(绿线)和纯几何匀滑作用下(红线)的金M带辐射流的P2不对称扰动幅度a2/a0(烧蚀面位置约300 μm,纯CH和掺杂层之间的界面位置在约650 μm处)
Figure 14. Radial distribution of 4π-averaged radiation temperature and gold M-band flux and P2 amplitude of gold M-band flux. Green lines are for the Si-doped capsule and blue lines for the Ge-doped capsule
图 16 HDC靶在P4不对称驱动源下DT/HDC物质界面的形变过程,图(a)为物质界面半径随时间的变化,图(b)为物质界面形变的P2分量(绿线)和P4分量(红线),实线和虚线分别是正、负P4扰动源的结果
Figure 16. The P0 (blue line (a)),P2 (green lines (b)),and P4 (red lines (b)) amplitudes of the fuel/ablator interface of an imploding HDC capsule driven by P4 perturbed X-ray drive. The dashed lines are the corresponding P2 (green) and P4 (red) distortion for a negatively P4 perturbed X-ray drive
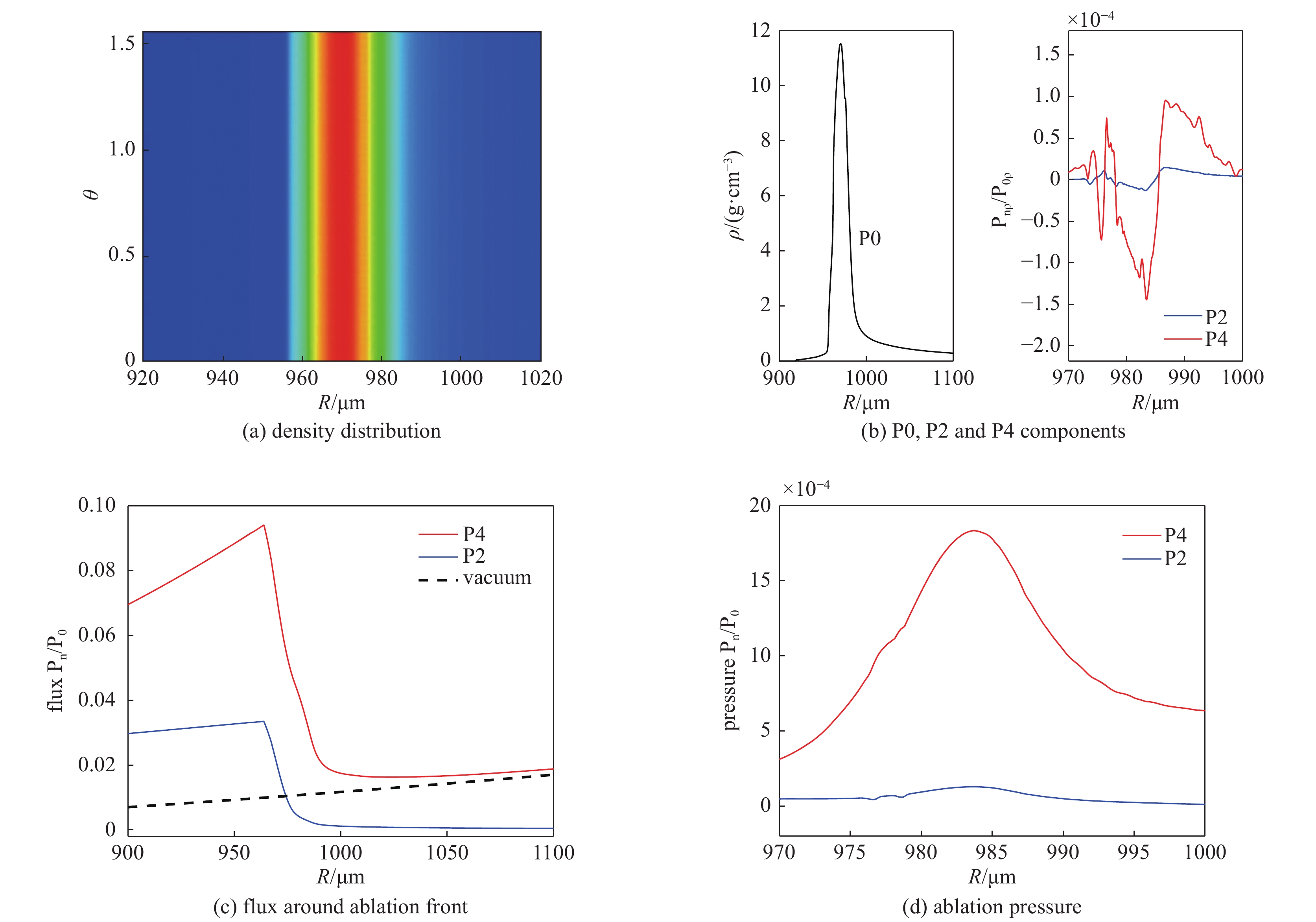
图 17 HDC靶丸在辐射源加P4扰动0.2 ns之后的靶丸响应。(a)为极坐标系中密度的二维分布;(b)黑线是密度分布勒让德展开的零阶量,红线和蓝线分别是P4和P2分量;(c)是烧蚀面附近辐射入流各界分量的分布,红线和蓝线分别是P4,P2分量,黑线是几何匀滑因子;(d)烧蚀压的P4和P2扰动
Figure 17. HDC capsule response to the P4 perturbed X-ray drive. (a) Density distribution in polar axis;(b) the black line shows the P0 component of the shell density,while the red and the blue lines show the P4 and P2 components,respectively;(c) the P2 and the P4 components of the ablating X-ray flux,the black dashed line shows the geometry smoothing factor for P4 asymmetric inward flux;(d) the P4 and the P2 components of the ablation pressure
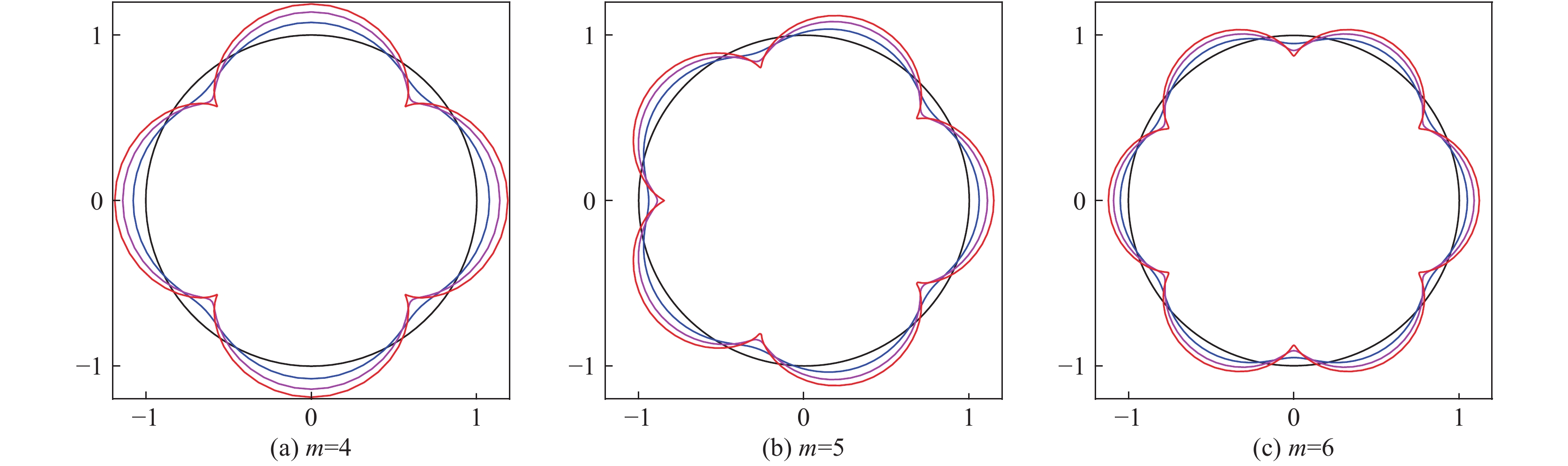
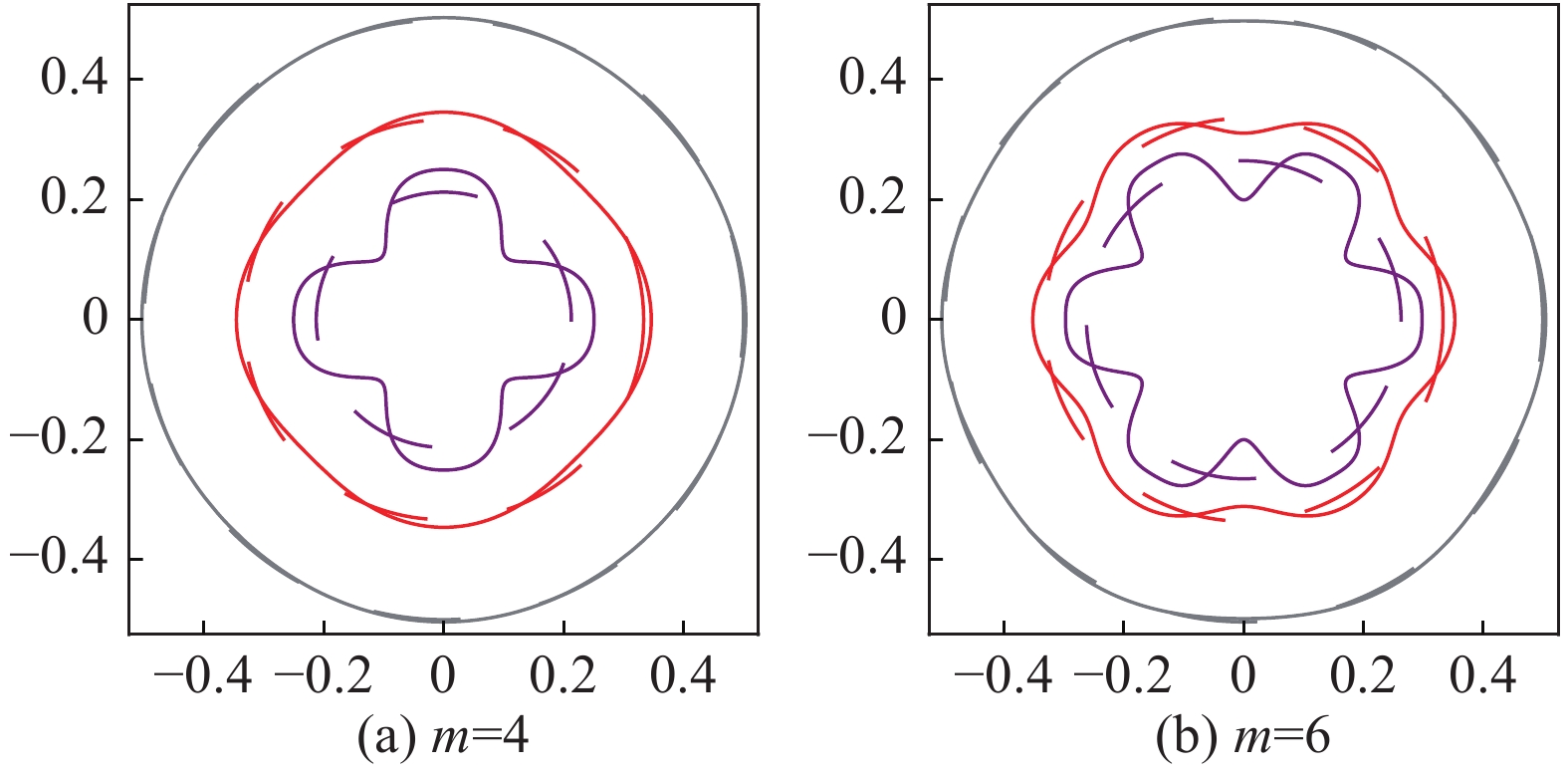
图 24 柱壳层单模扰动在γt=4.0,5.0和5.8的位置,模数(a)m=4,(b)m=5,和(c)m=6. 参数:g=1,r0=1,λ0=2πr0/m和η0=0.001λ0
Figure 24. Temporal evolution of the cylindrical shell position with the initial single-mode perturbation for (a) m=4,(b) m=5, and (c) m=6 at γt=4.0,5.0 and 5.8. The parameters are g=1,r0=1,λ0=2πr0/m and η0=0.001λ0
图 25 (a)比较壳层模型由数值计算的线性增长率与线性化、经典形式和Mikaelian理论结果,参数:g=1和r0=1;(b)比较壳层模型、线性理论和WNL模型的气泡-尖钉幅值的演化,参数:m=4和η0/r0=0.016
Figure 25. (a) Comparison of the linear growth rate obtained from the numerical solutions and linearized result of thin shell model,classical formula and Mikaelian’s theory. The parameters are g=1 and r0=1.(b) Comparison of the averaged amplitudes of bubble and spike obtained from the thin shell model,linear theory and WNL model. The parameters are m=4 and η0/r0=0.016
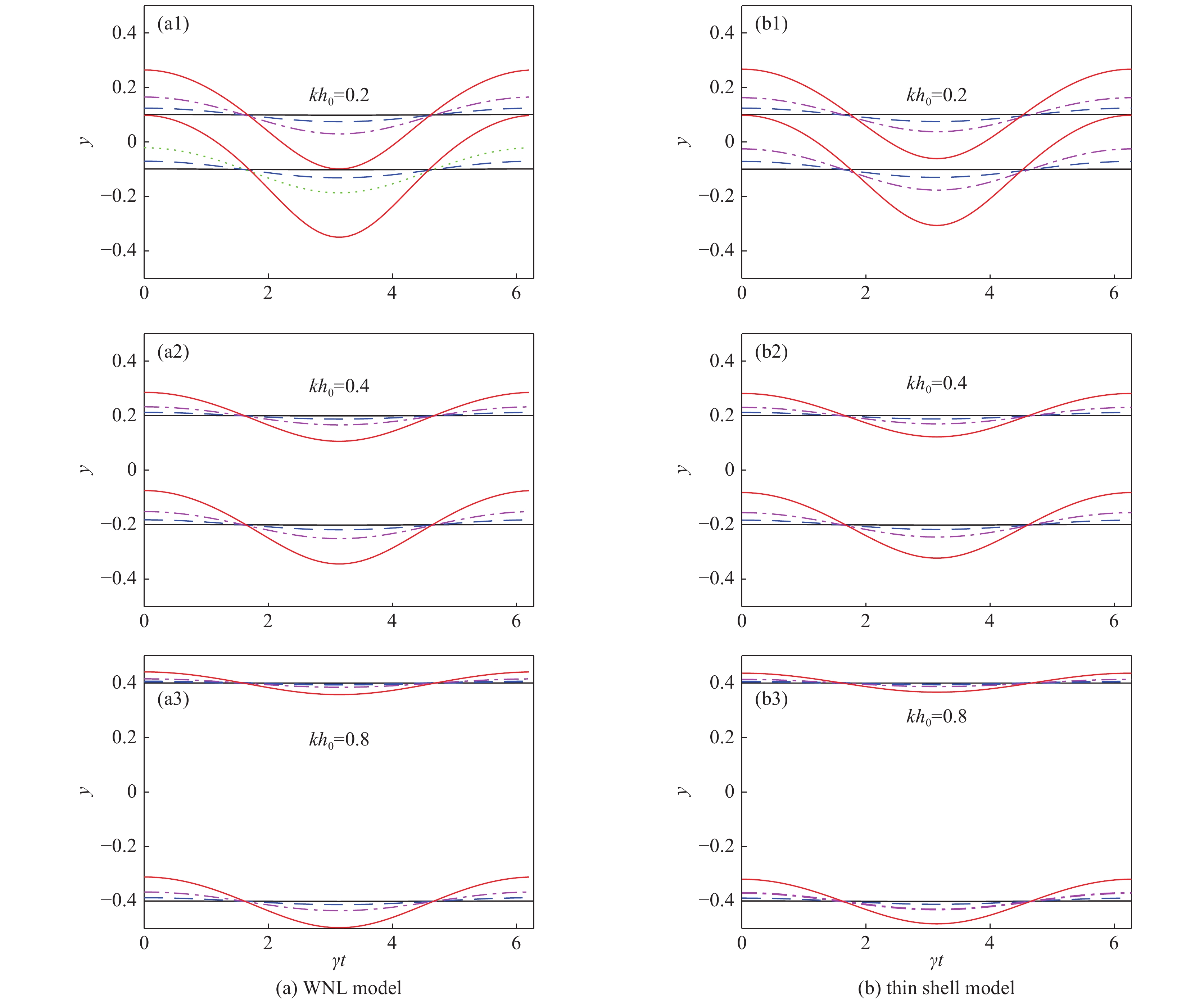
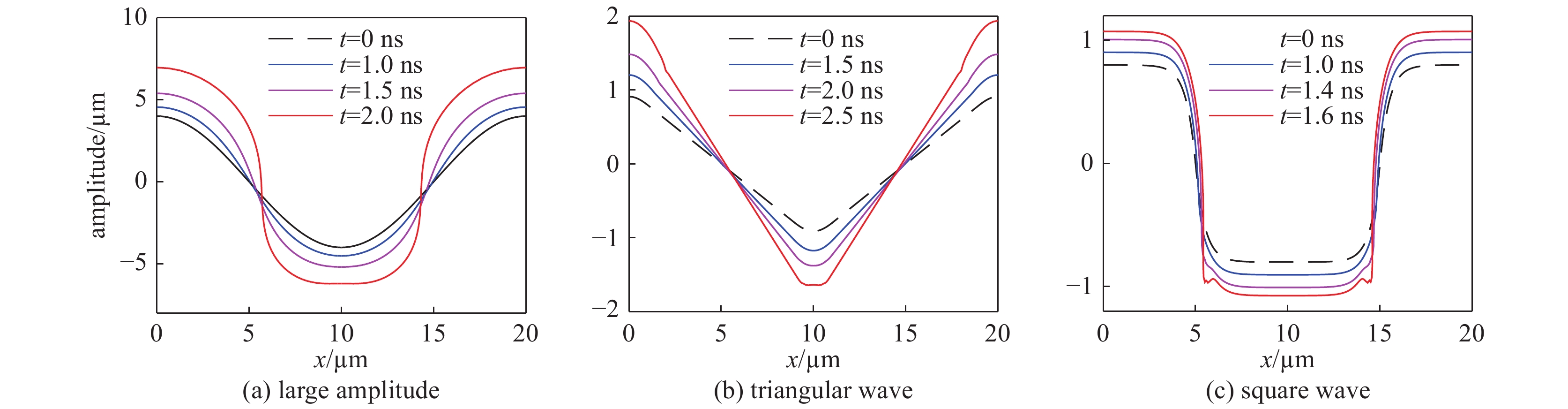
图 26 壳层模型应用于(a)初始大幅值、(b)高斯波形和(c)方波在不同时间的扰动界面。参数:g=1,r0=1,(a)η0=0.15λ0,(b)η0=0.05λ0,and(c)η0=0.2λ0
Figure 26. Cylindrical shell positions for (a) the initial large amplitude,(b) Gaussian type perturbation and (c) square perturbation at different time. The parameters are g=1,r0=1,(a) η0=0.15λ0,(b) η0=0.05λ0,and (c) η0=0.2λ0 respectively
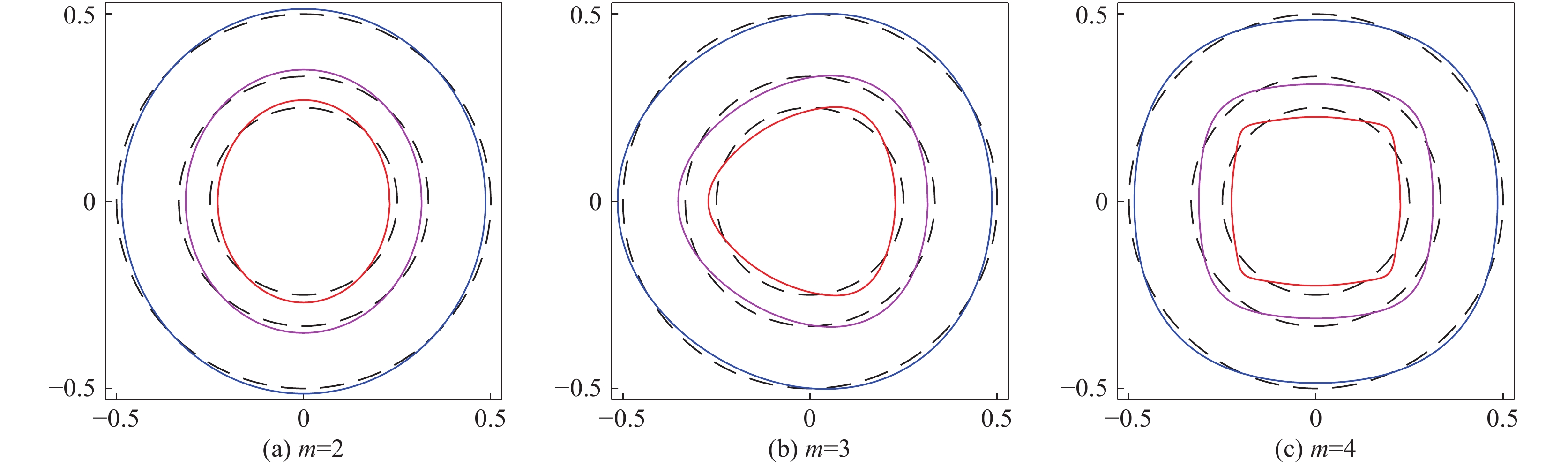
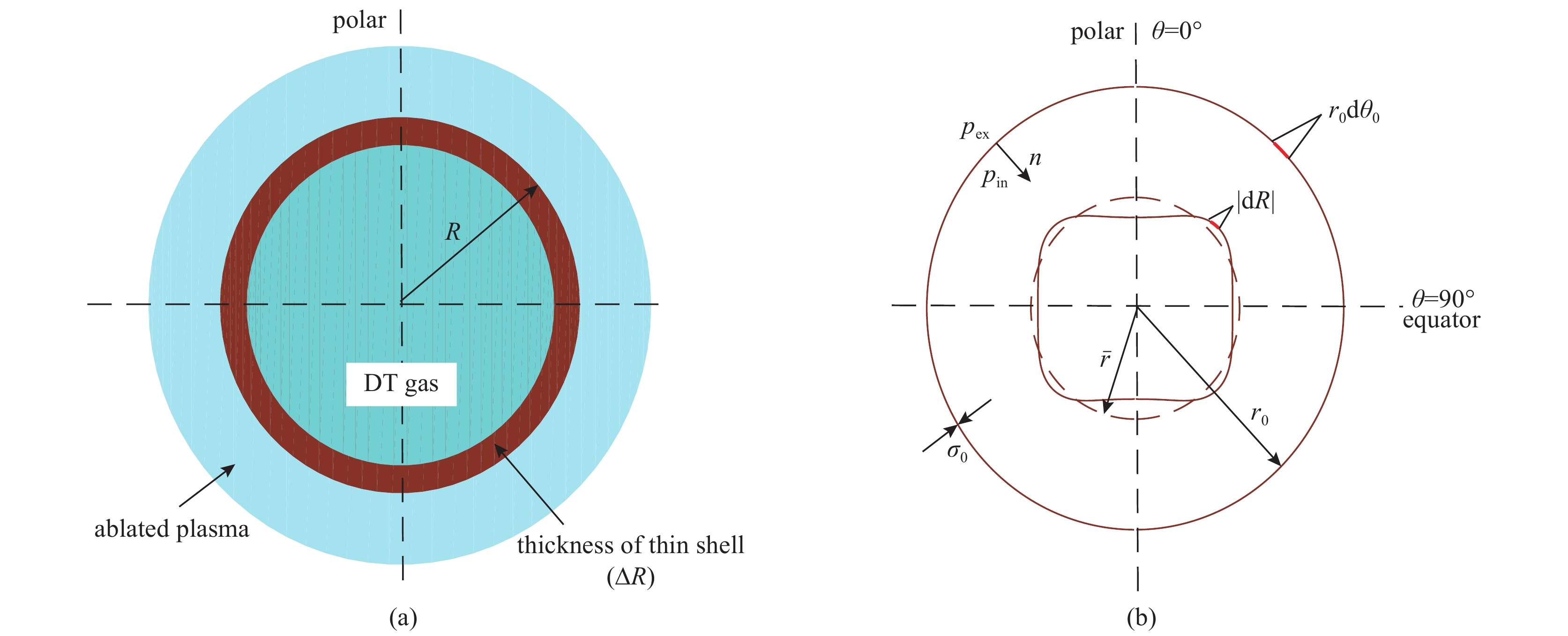
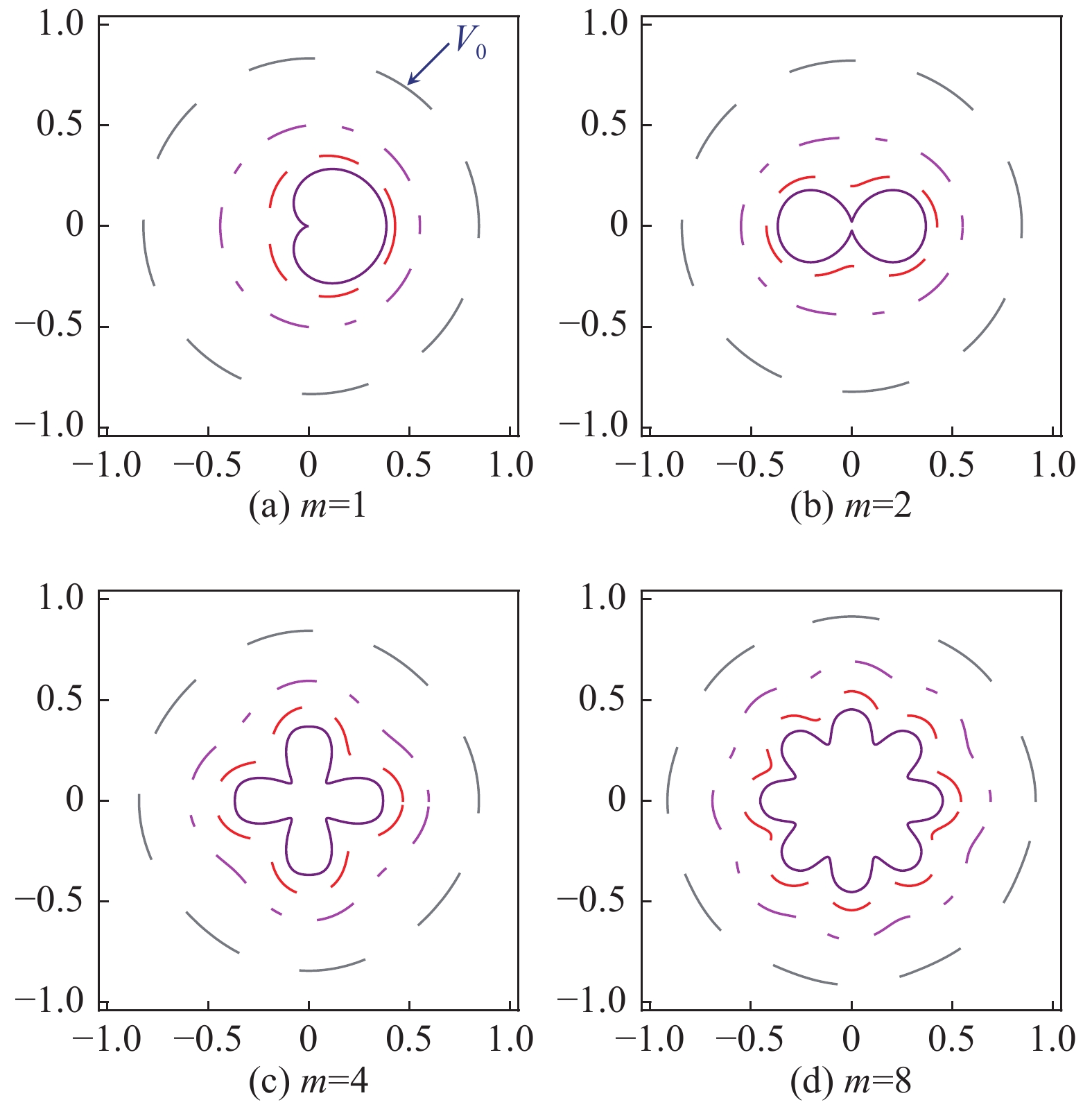
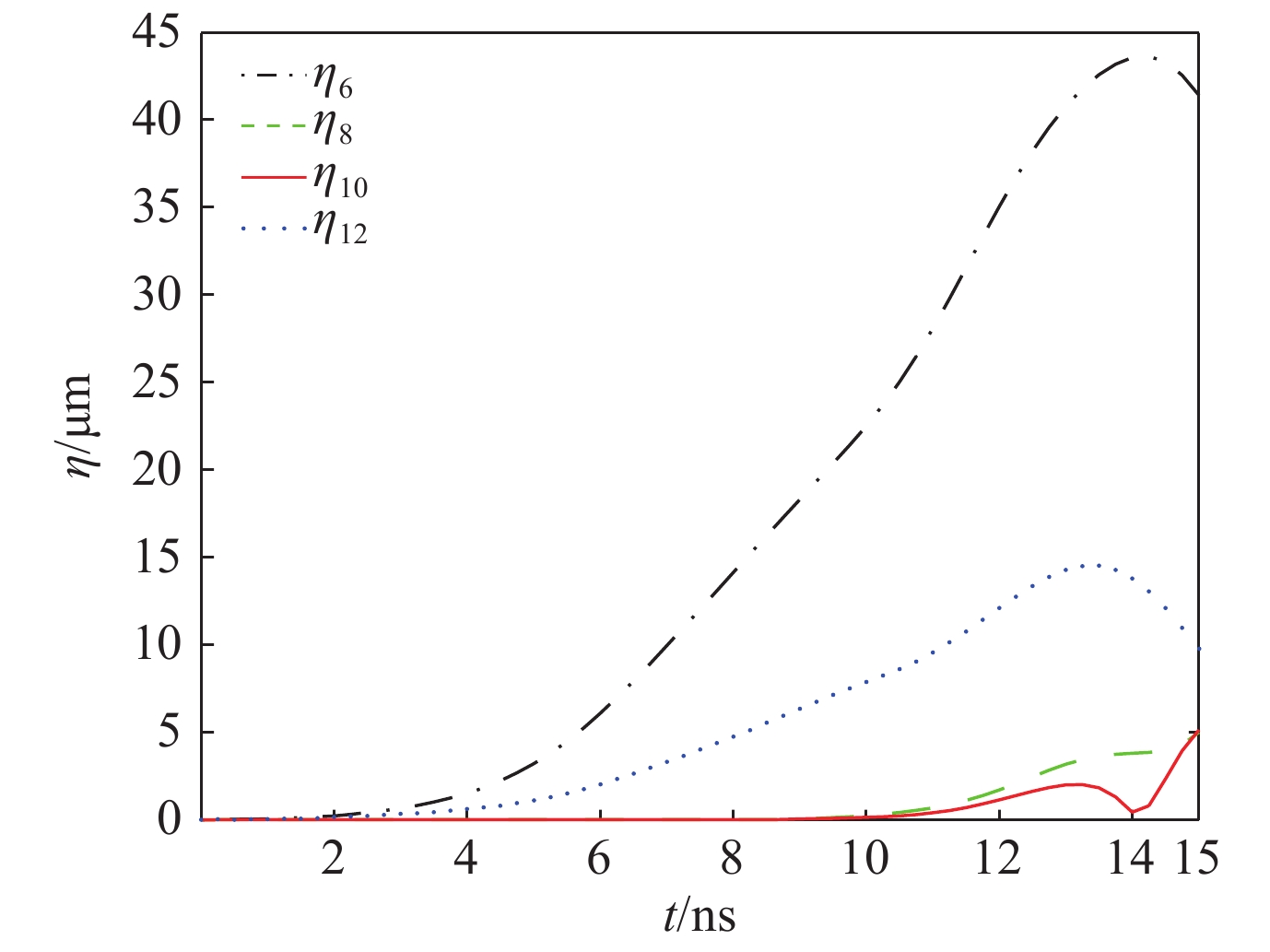
图 27 柱壳层受单模态驱动不对称性(a)m=2,(b)m=3和(c)m=4在收缩比CR为2,3和4时的形变。参数:r0=1,p0=1,σ0=1和空间调制比例A0=0.03
Figure 27. Temporal evolution of the cylindrical thin shell positions for the drive asymmetry with the single-mode spatial modulation (a) m=2, (b) m=3 and (c) m=4 when convergence ratio is 2,3,and 4. The parameters are r0=1,p0=1,σ0=1,and A0=0.03
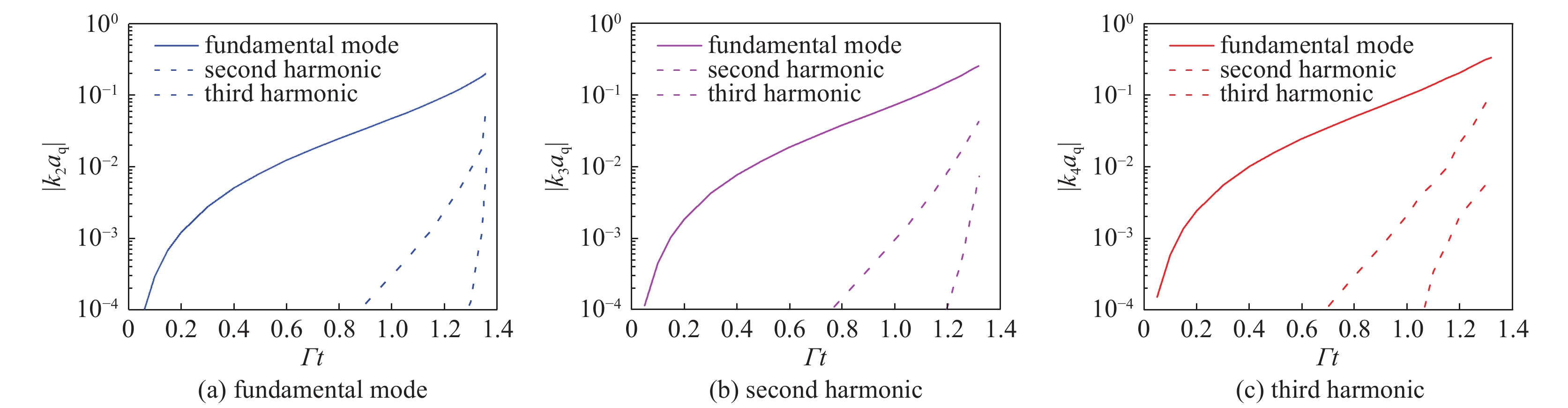
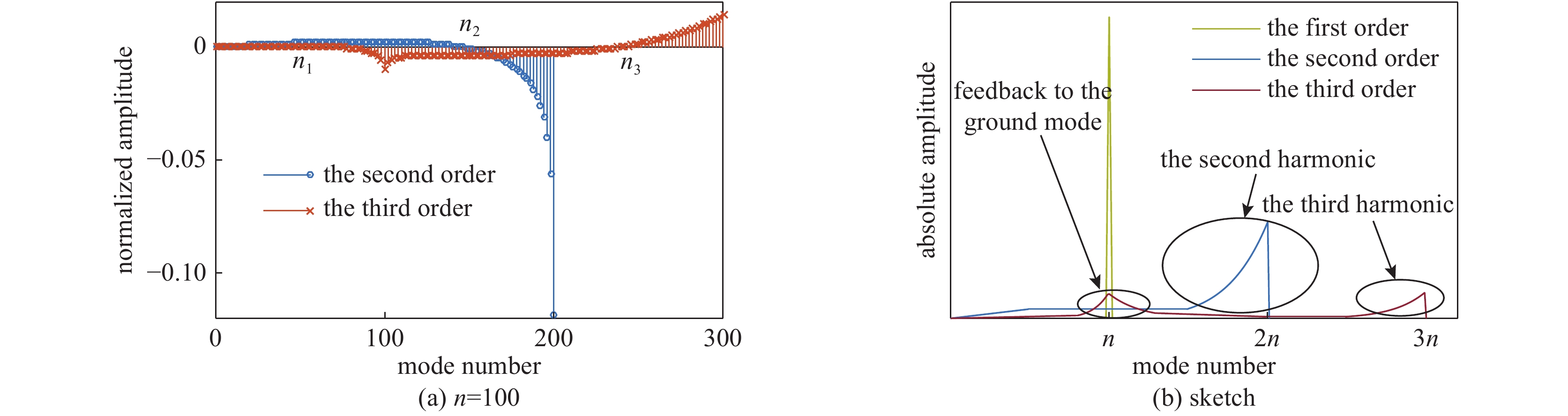
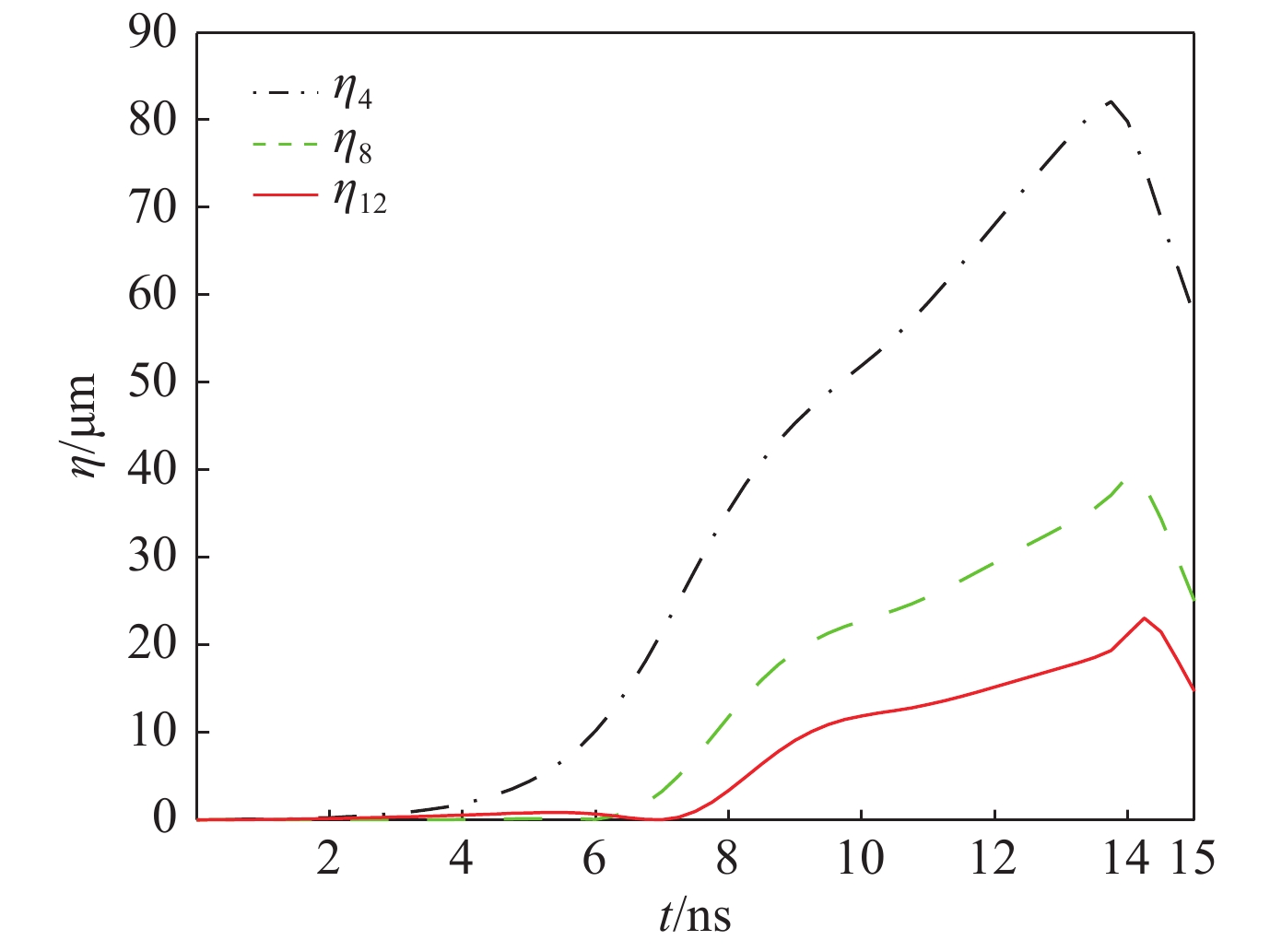
图 28 柱几何驱动不对称性中壳层形变的基模、二次谐波和三次谐波的演化。参数同图27。
Figure 28. Temporal evolution of normalized amplitudes of the fundamental mode,second harmonic and third harmonic of the cylindrical thin shell for the drive asymmetry with single-mode spatial modulation respectively. The parameters are the same as the data of Fig.27
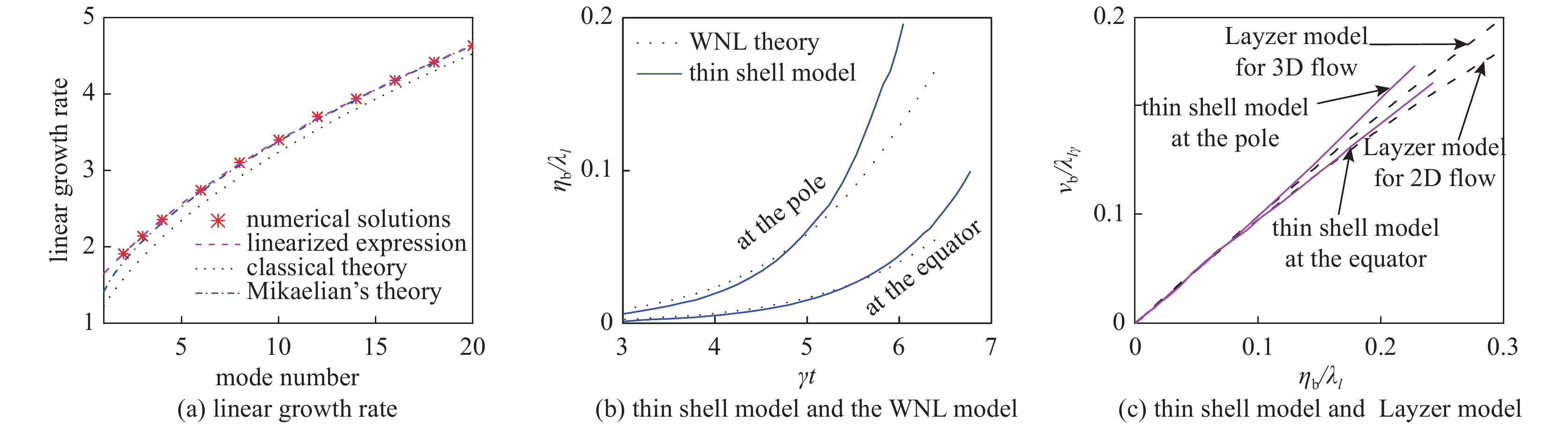
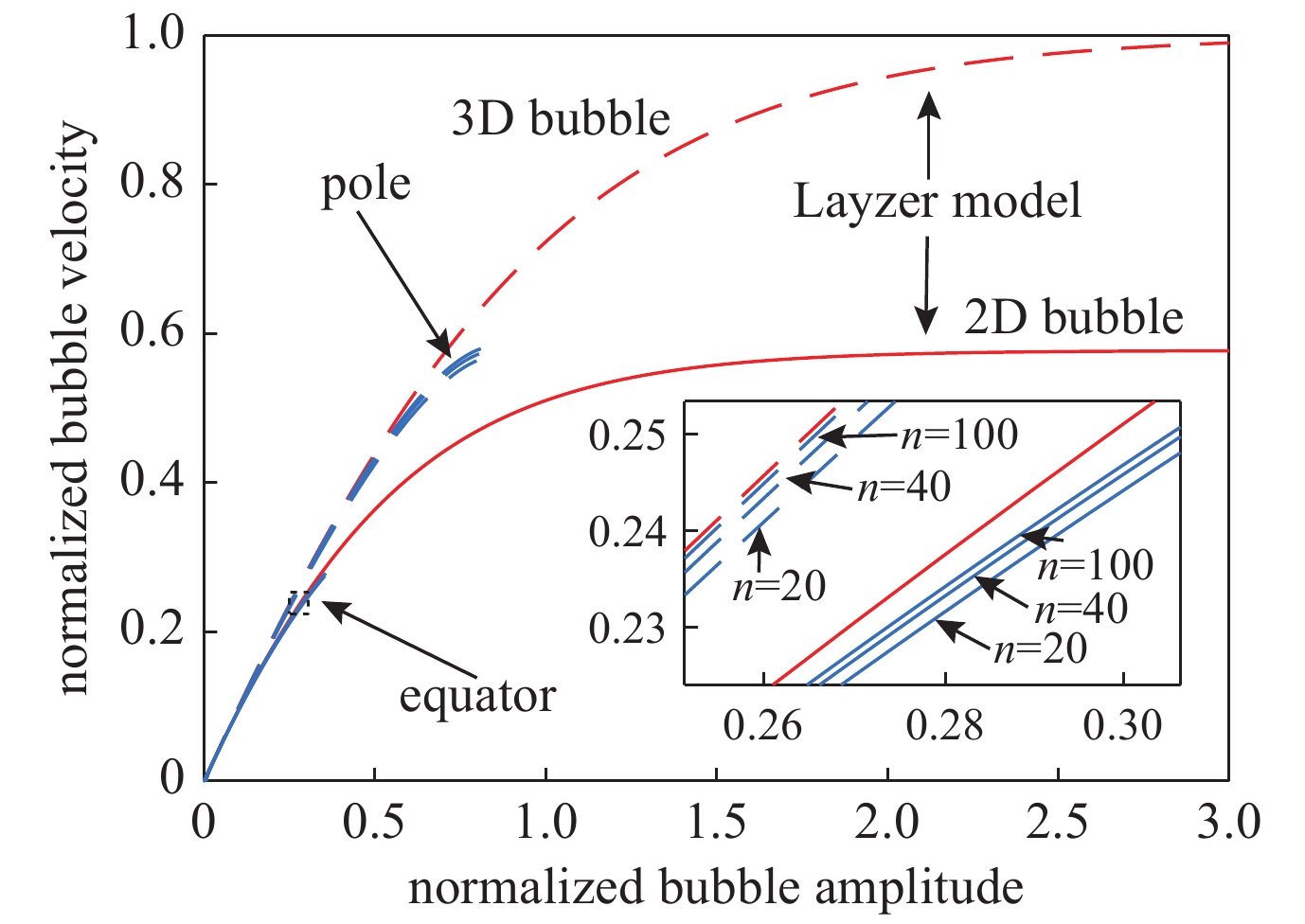
图 30 (a)比较壳层模型由数值计算的线性增长率与线性化、经典理论和Mikaelian理论结果;(b)比较壳层模型和WNL模型在极轴和赤道处的幅值演化;(c)比较壳层模型和Layzer模型在赤道和极轴处的气泡速度。参数g=1,r0=1,and A0=0.001λ1
Figure 30. (a) Comparison of the linear growth rate obtained from the numerical solutions and linearized results of thin shell model,classical theory and Mikaelian’s theory. (b) Comparison of the perturbed amplitude of the thin shell model with that of the WNL model for the initial perturbation at the d equator,respectively. (c) Comparison of the bubble velocities of the pole and equator obtained from the thin shell model and those from Layzer model for 3D axisymmetries bubble and 2D bubble. The parameters are g=1,r0=1,and A0=0.001λ1
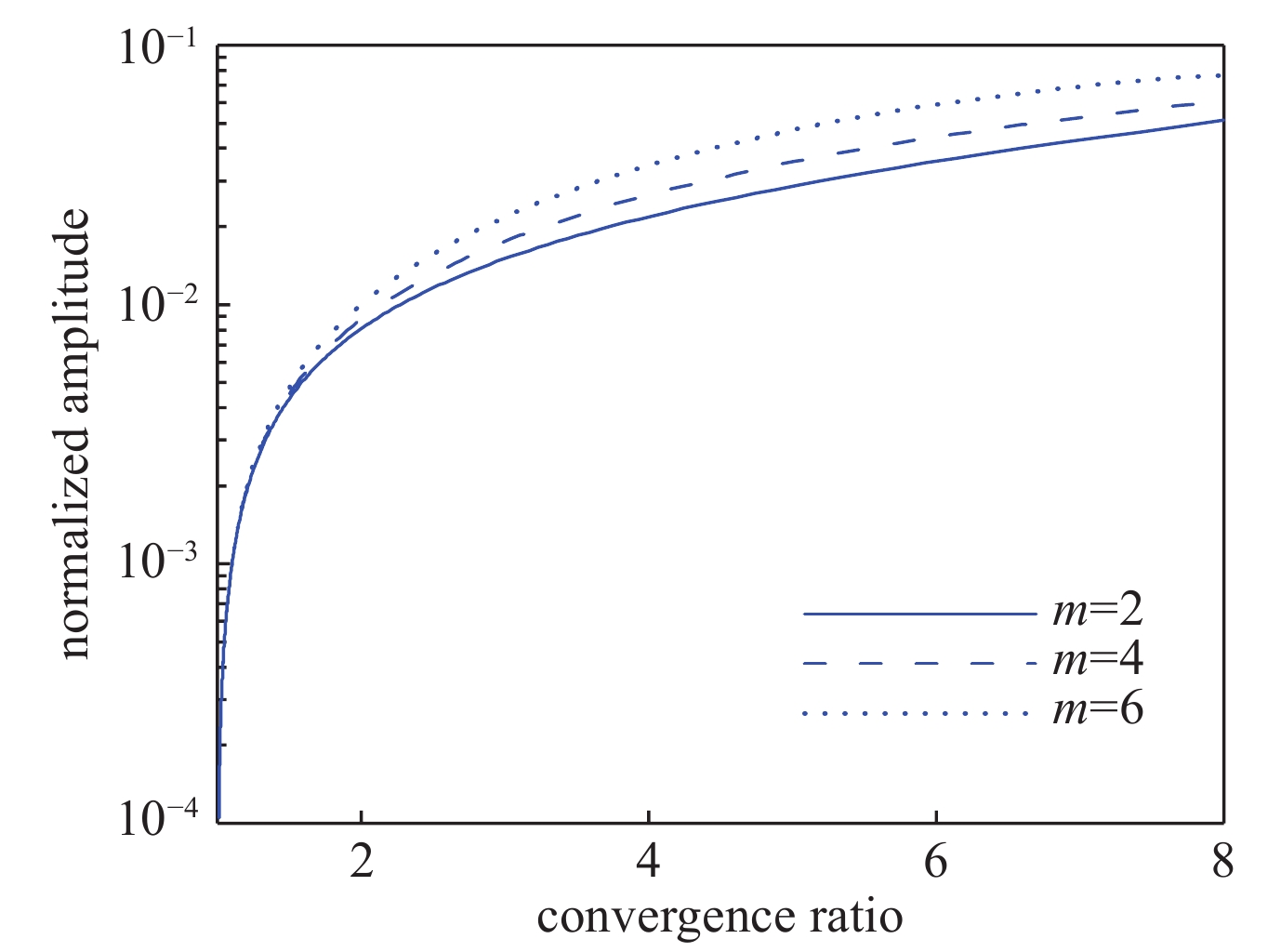
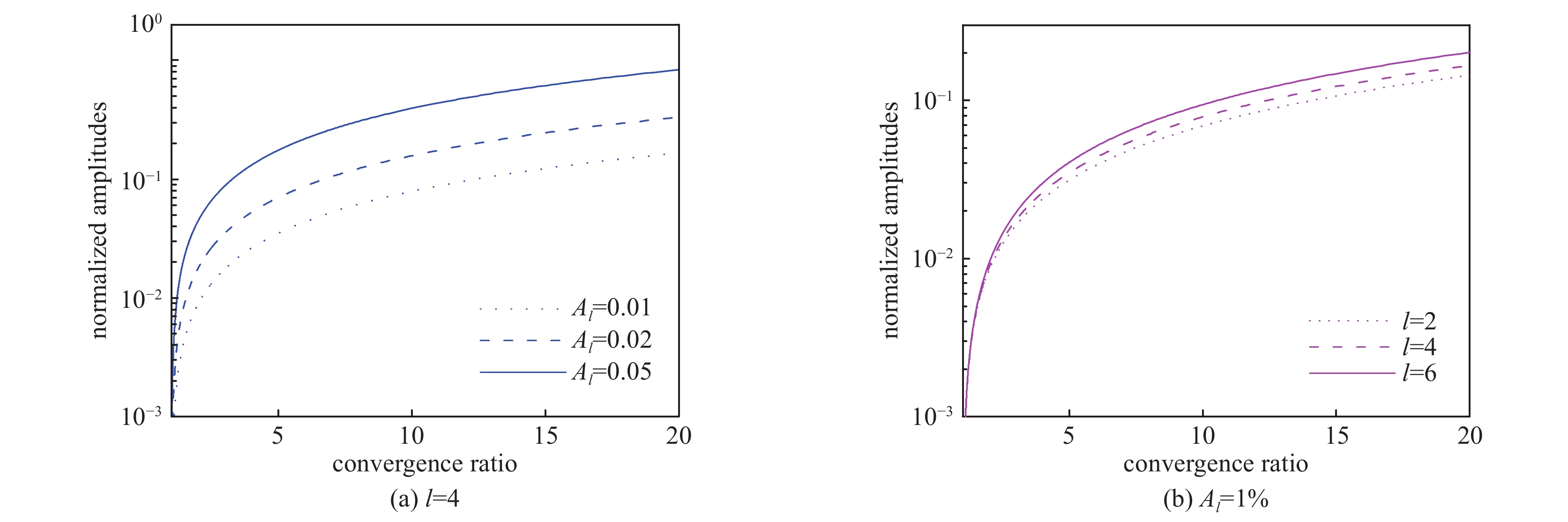
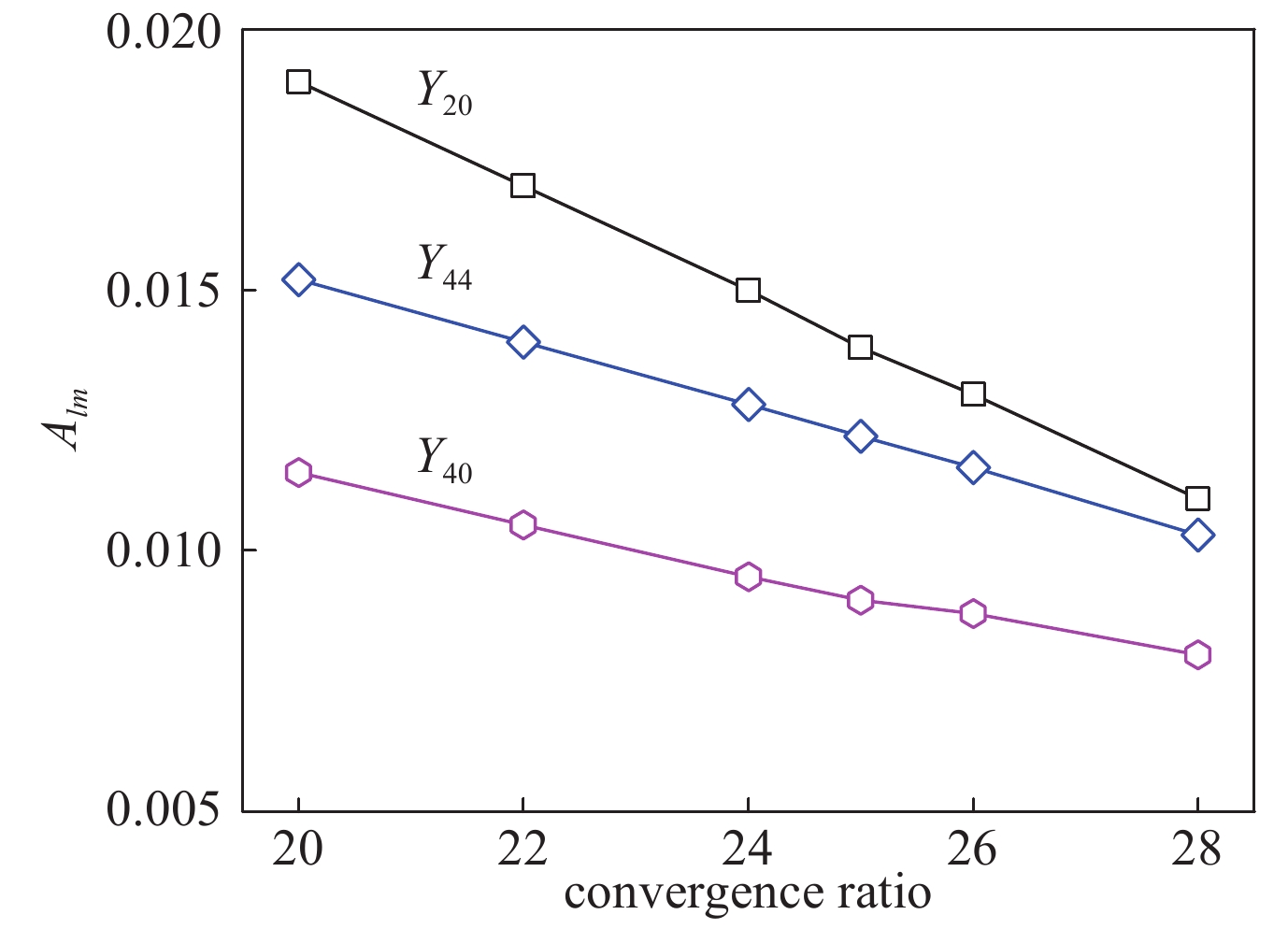
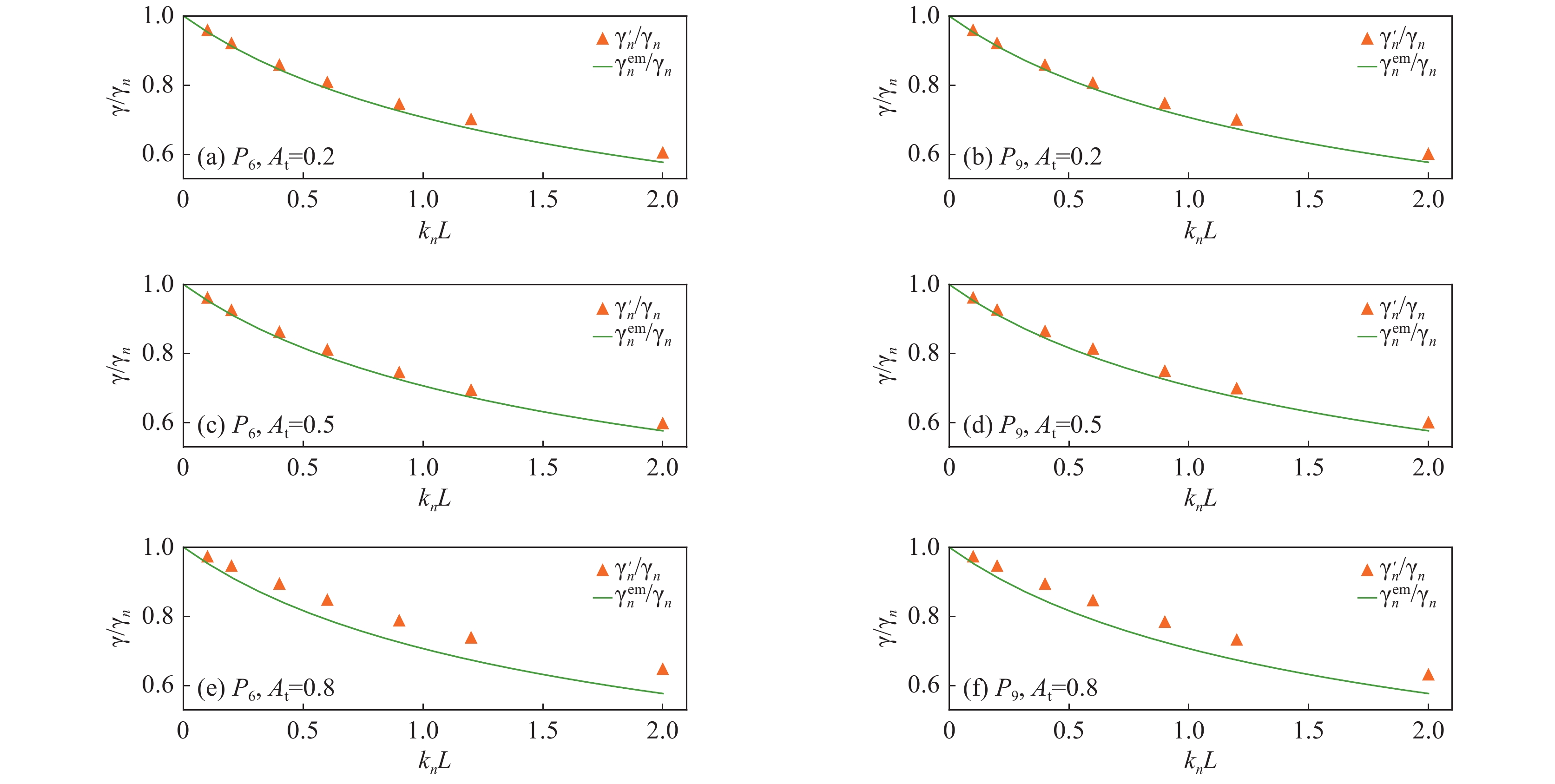
图 33 壳层线性幅值随收缩比的关系,(a)相同模数l=4时的不同空间调制比例和(b)相同空间调制比例Al=1%时不同调制模数。参数:r0=870 μm,σ0=21.8955 g/μm and
${\bar p_{{\rm{in0}}}}$ =10 GPaFigure 33. Variation of the normalized linear amplitudes in the radial direction with the convergence ratio for (a) the spatial modulation ratio with l=4 and (b) the spatial modulation mode with Al
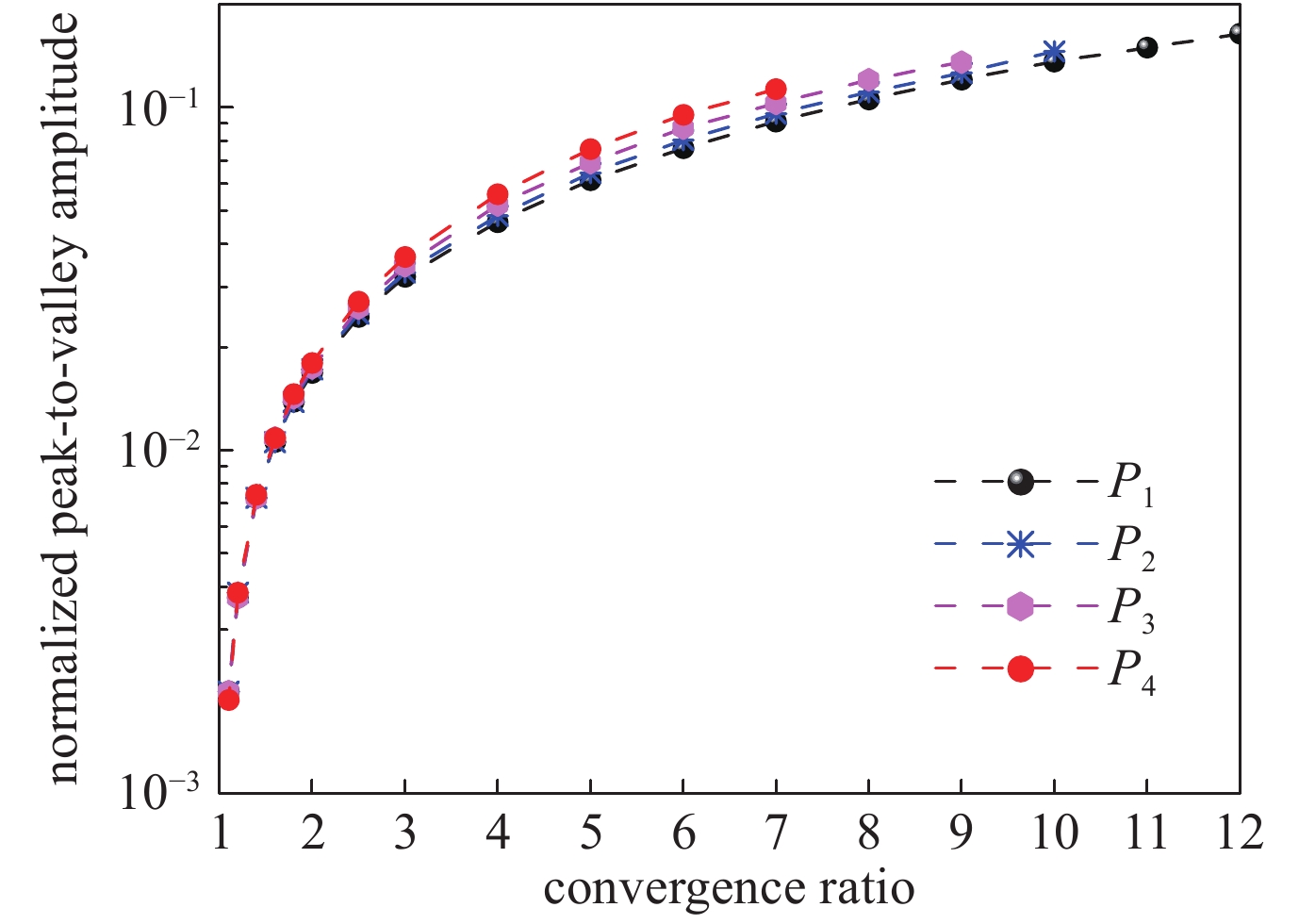
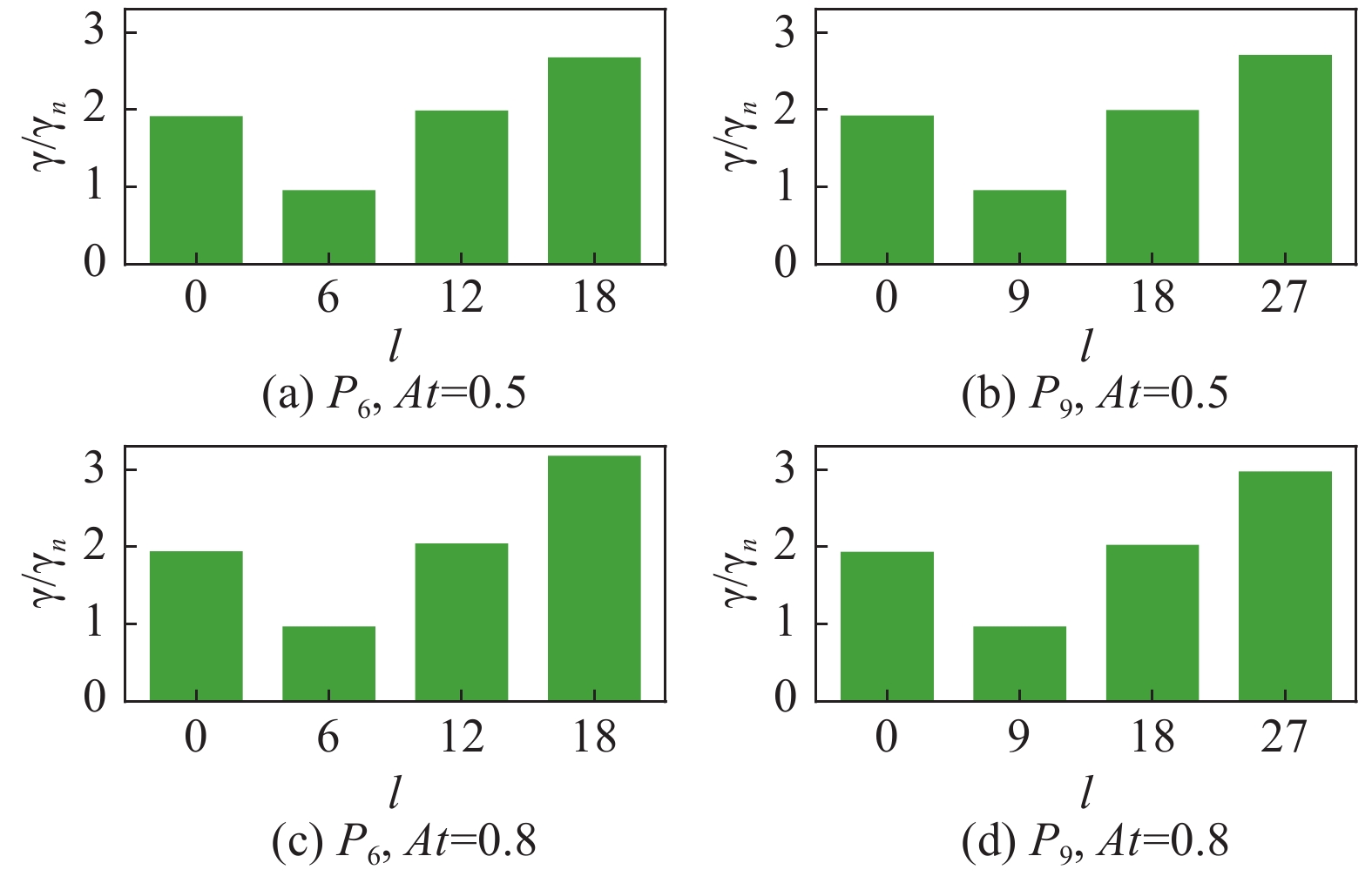
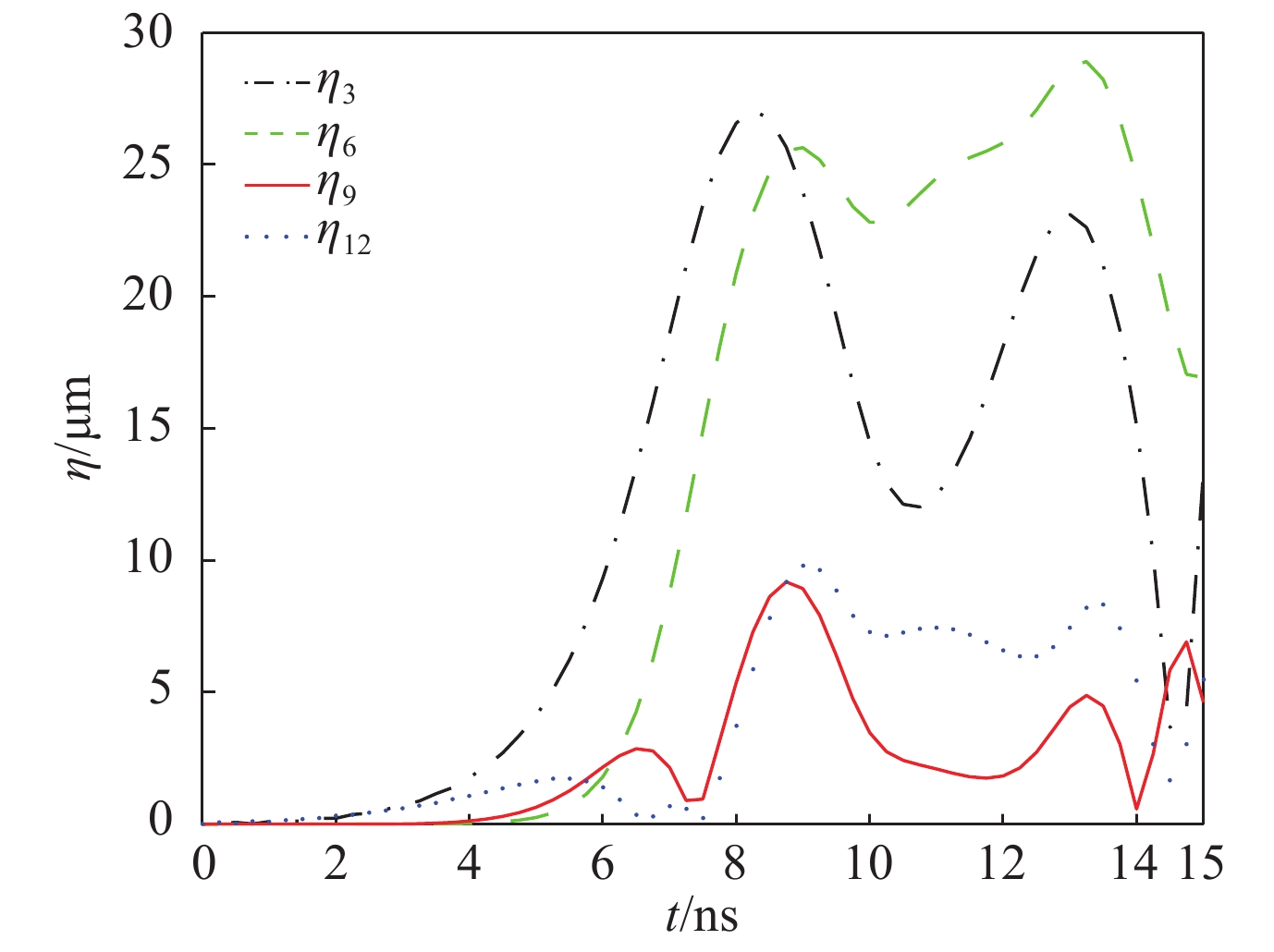
=1%. The parameters are r0=870 μm,σ0=21.8955 g/μm and ${\bar p_{{\rm{in0}}}}$ =10 GPa图 34 壳层波峰-波谷幅值在低阶模驱动不对称满足
${A_1} = 3{A_2}/4 = {A_3} = 5{A_2}/7$ 的演化。参数:${r_0}$ =870 μm, σ0=21.8955 g/μm,${\bar p_{{\rm{in0}}}}$ =10 GPa和A4=1%Figure 34. Temporal evolution of normalized peak-to-valley amplitudesfor the low-mode drive asymmetry with
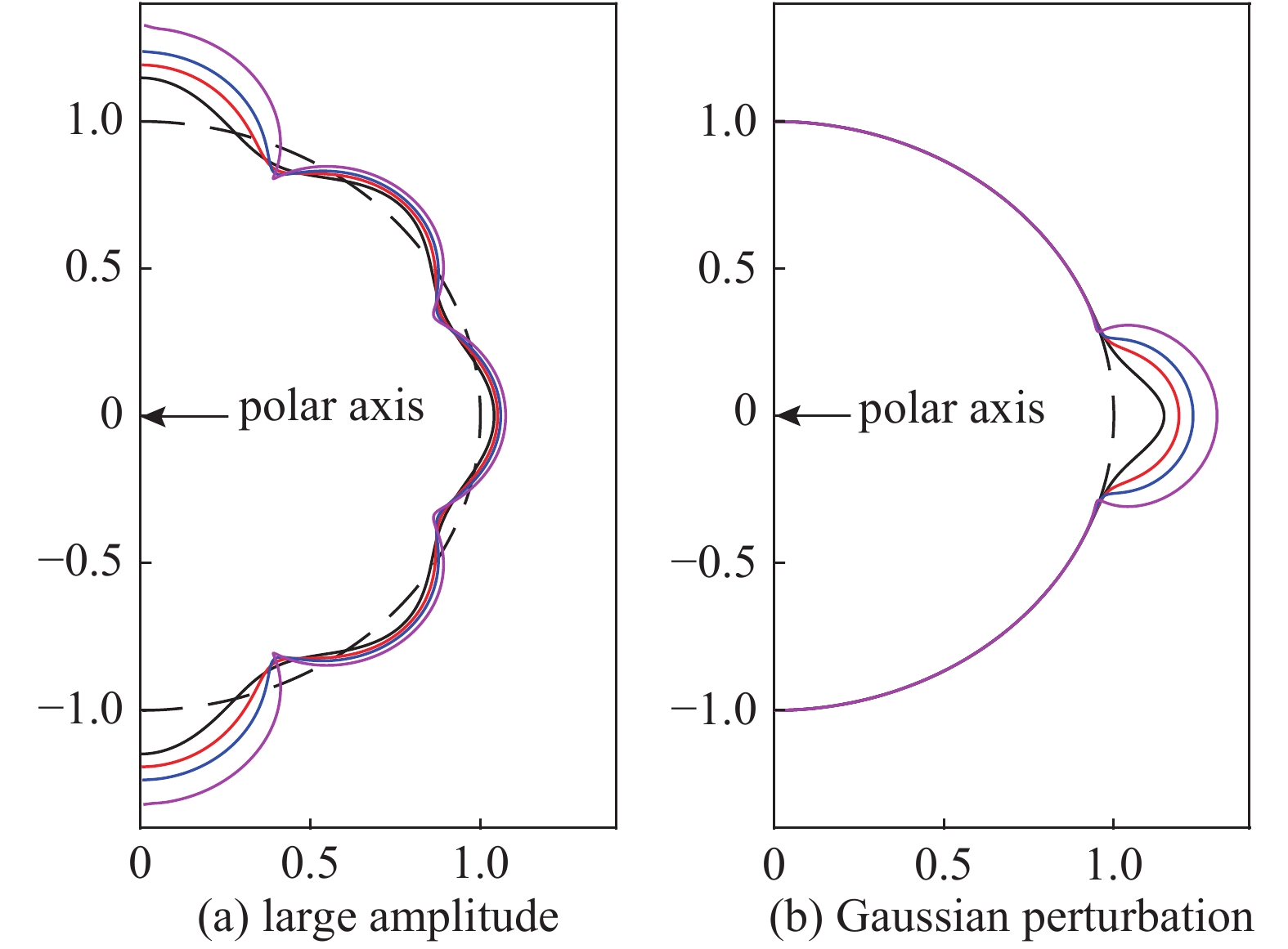
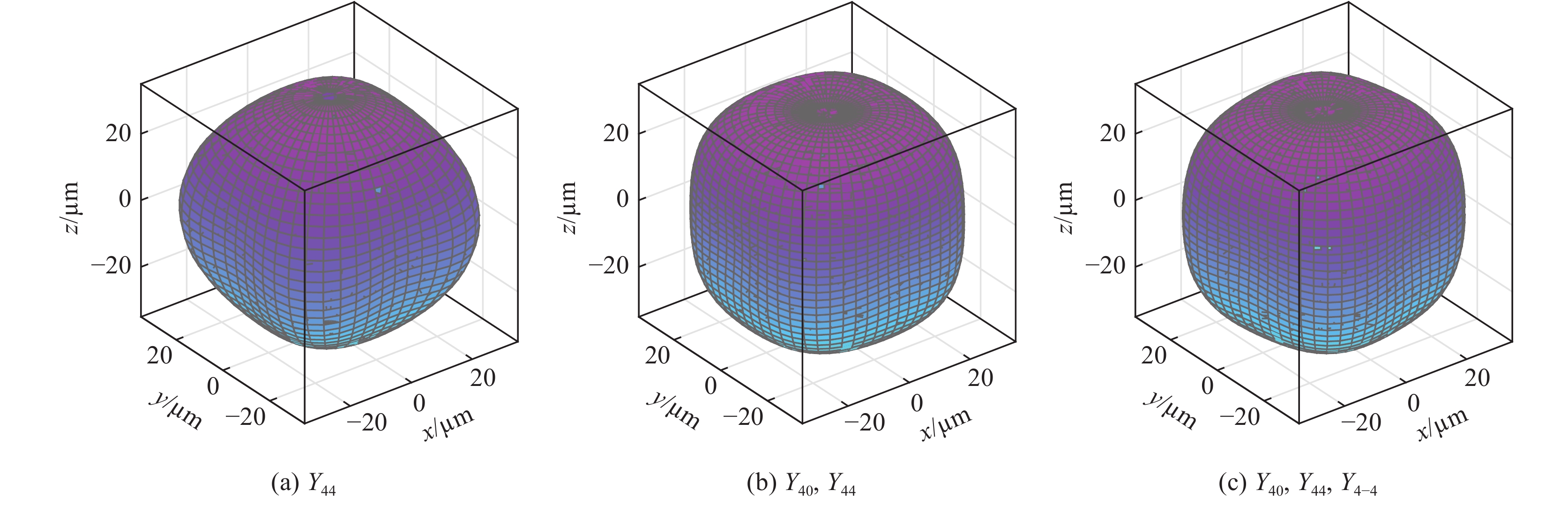
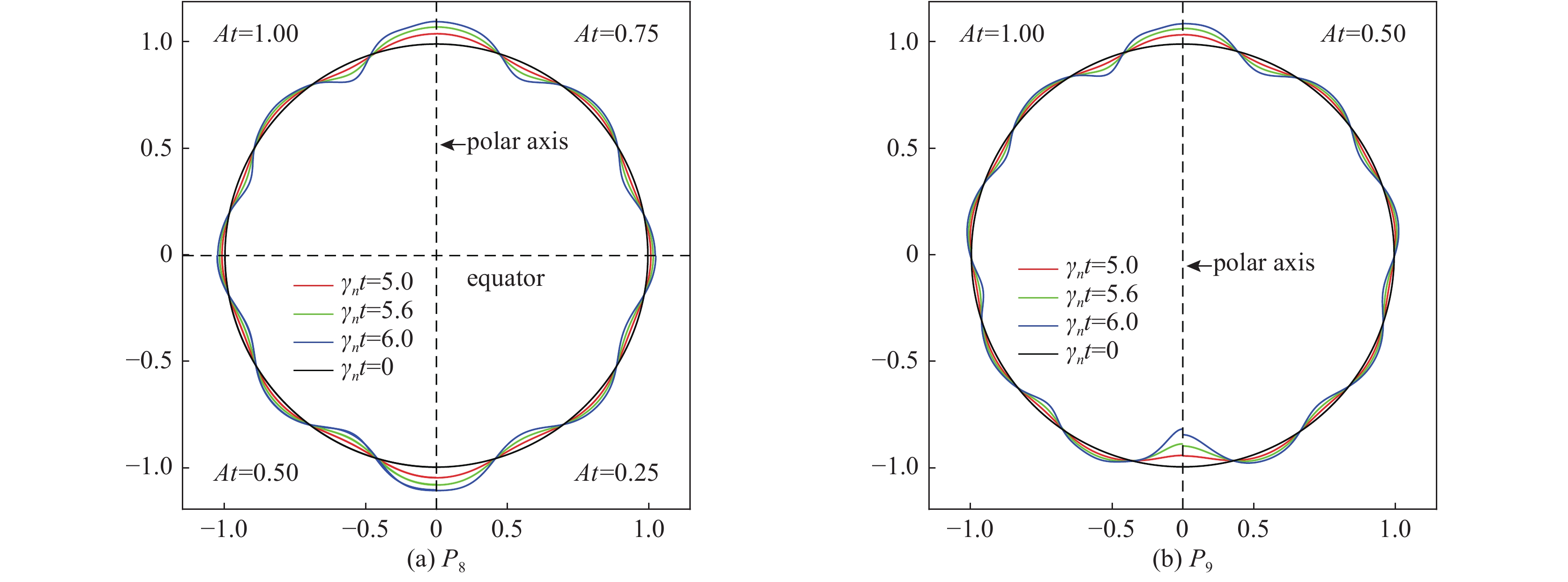
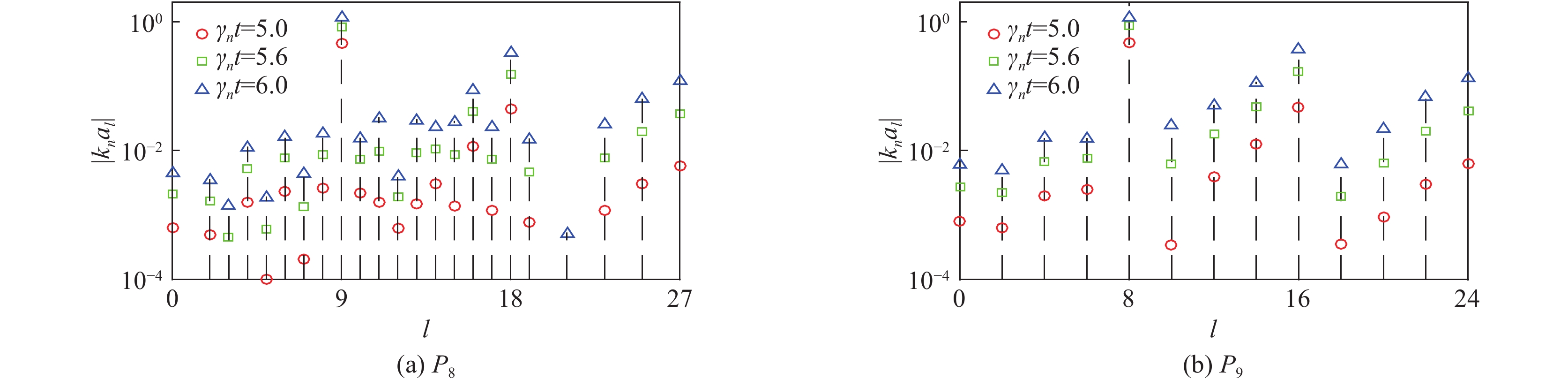
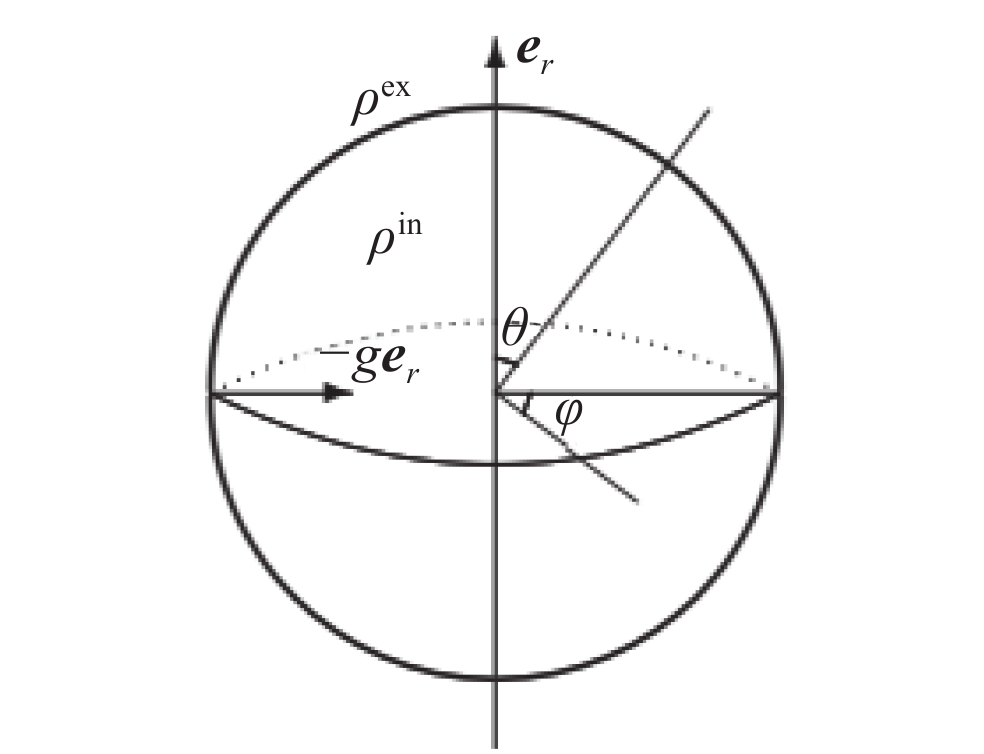
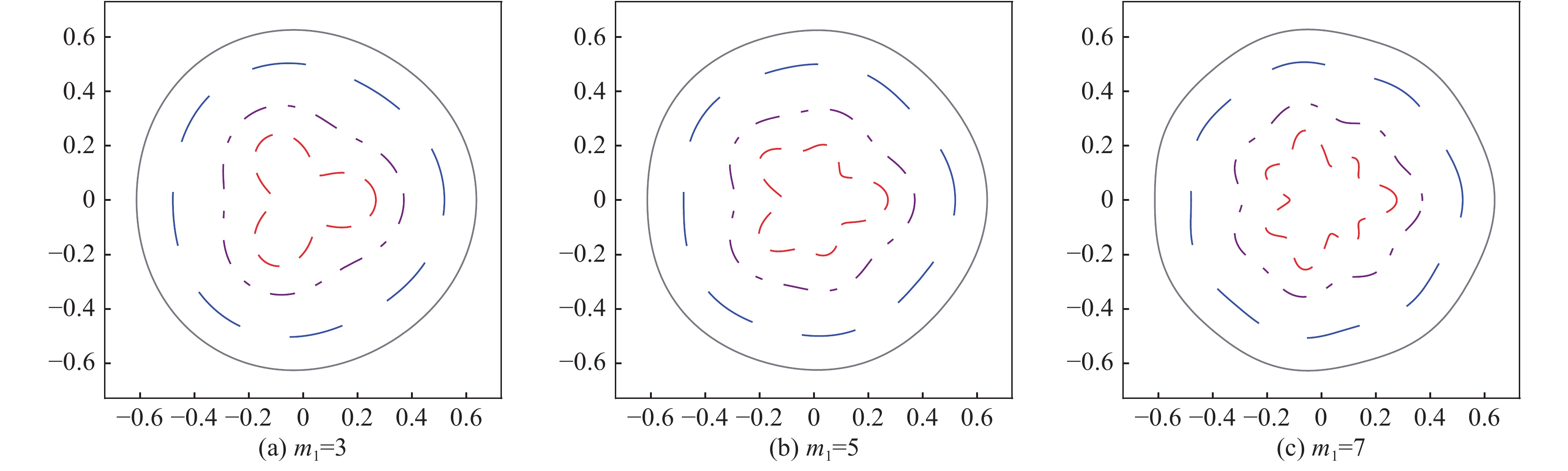
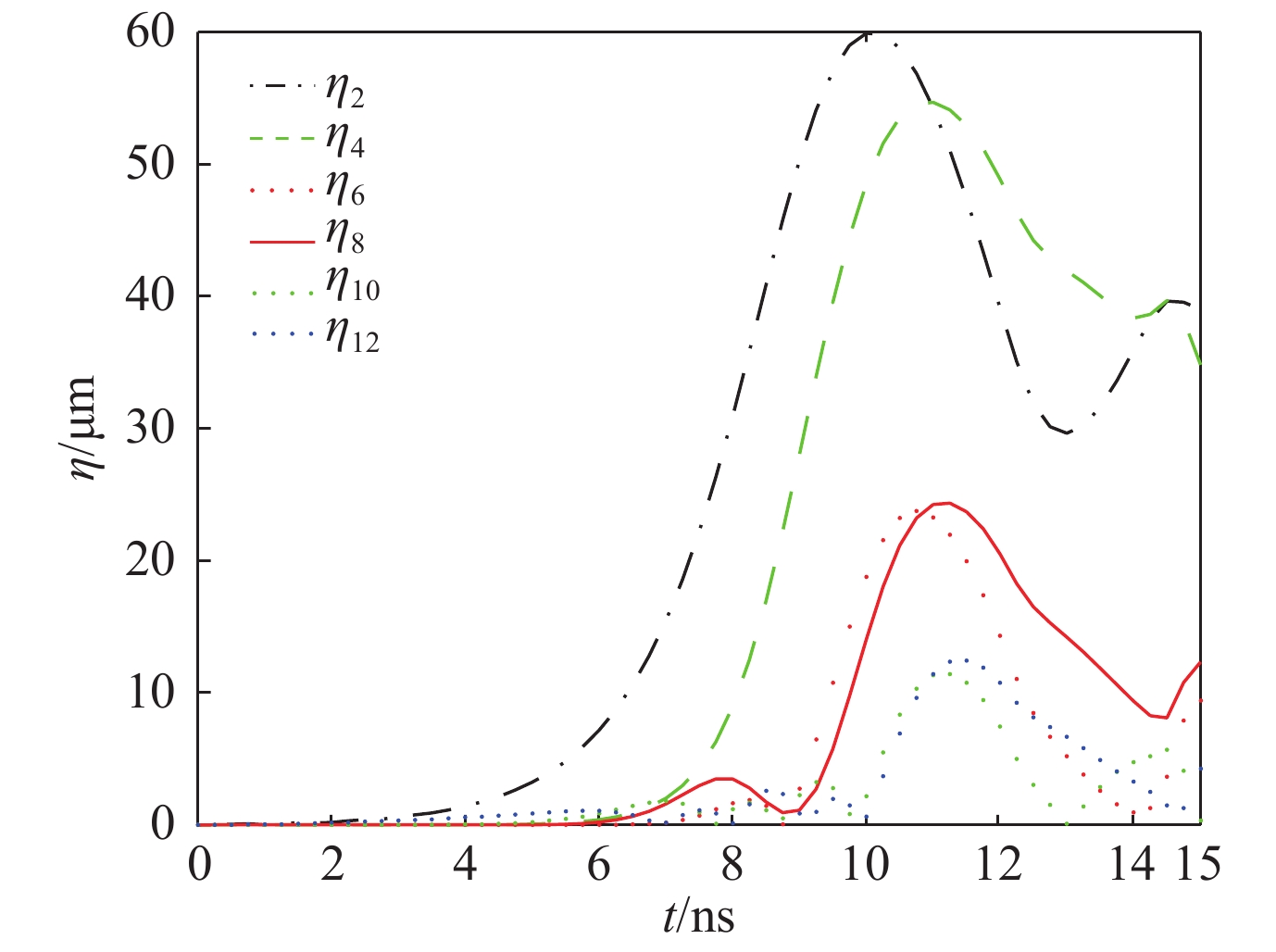
${A_1} = 3{A_2}/4 = {A_3} = 5{A_2}/7$ . The parameters are${r_0}$ =870 μm, σ0=21.8955 g/μm,${\bar p_{{\rm{in0}}}}$ =10 GPa,and A4=1%图 36 三维球几何壳层(a)单模态
${Y_{44}}$ ,(b)双模态${Y_{40}}$ ,${Y_{44}}$ ,和(c)三模态${Y_{40}}$ ,${Y_{44}}$ ,${Y_{4{\rm{ - }}4}}$ 的驱动不对称性具有等效压强在收缩比25时的变形。参数:${r_0} = 870\;{\rm{{\text{µ}} m}}$ ,${p_{{\rm{ex0}}}}$ =1100 GPar,${p_{{\rm{in0}}}}$ =0.4 GPa,${\gamma _{\rm{h}}}$ =5/3,${\rho _{{\rm{DT}}}}{\rm{ = }}0.25\;{\rm{g/c}}{{\rm{m}}^3}$ ,$\Delta R = 80\;{\rm{{\text{µ}} m}}$ ,and${A_{44}}$ =0.01Figure 36. Temporal evolution of three-dimensional spherical thin shell positions for the drive asymmetry with (a)single-mode
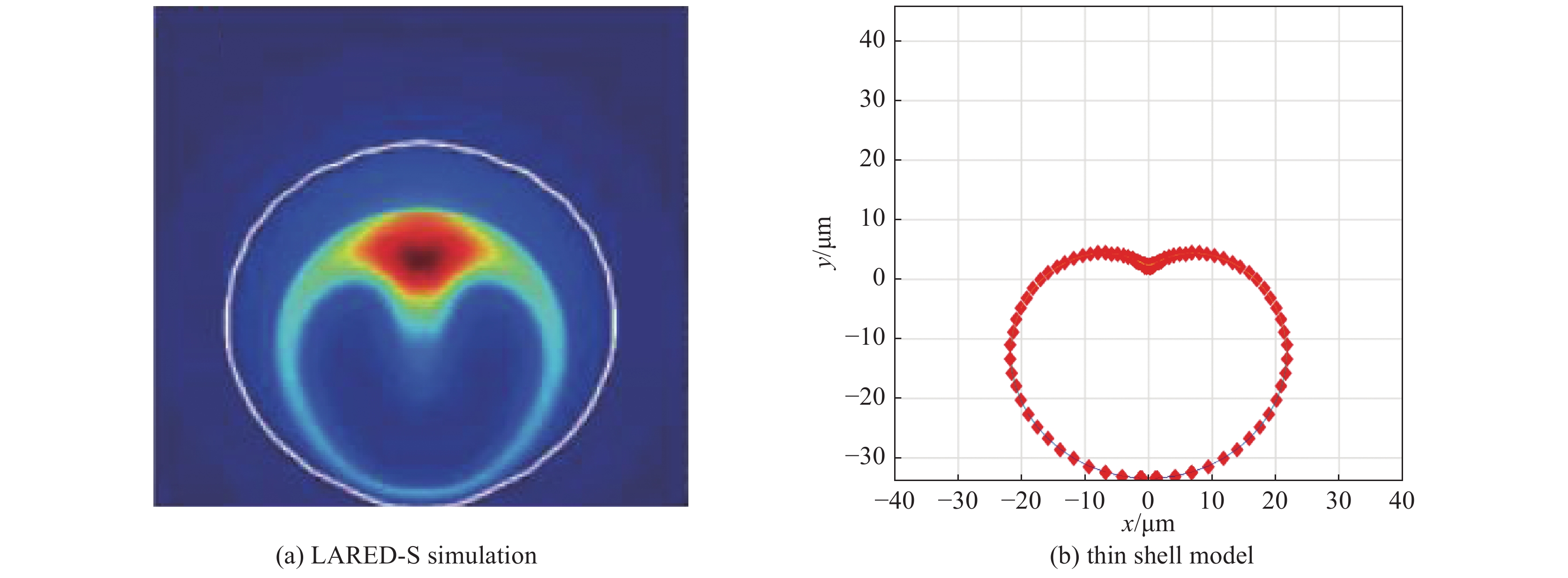
${Y_{44}}$ ,(b) two-modes${Y_{40}}$ ,${Y_{44}}$ and (c) three-modes${Y_{40}}$ ,${Y_{44}}$ ,${Y_{4{\rm{ - }}4}}$ spatial modulation at convergence ratio 25. The parameters are${r_0} = 870\;{\rm{{\text{µ}} m}}$ ,${p_{{\rm{ex0}}}}$ =1100 GPa,${p_{{\rm{in0}}}}$ =0.4 GPa,${\gamma _{\rm{h}}}$ =5/3,${\rho _{{\rm{DT}}}}{\rm{ = }}0.25 \;{\rm{g/c}}{{\rm{m}}^3}$ ,$\Delta R = 80\;{\rm{{\text{µ}} m}}$ ,and${A_{44}}$ =0.01图 38 激光聚变内爆物理实验数值模拟重建的热斑[(a),(b)和(c)]和壳层模型[(d),(e)和(f)]结果的比对
Figure 38. Comparison between the physical experiment [(a),(b) and (c)][22] and the thin shell model [(d), (e) and (f)] for the deformation of the hot-spot in ICF implosion
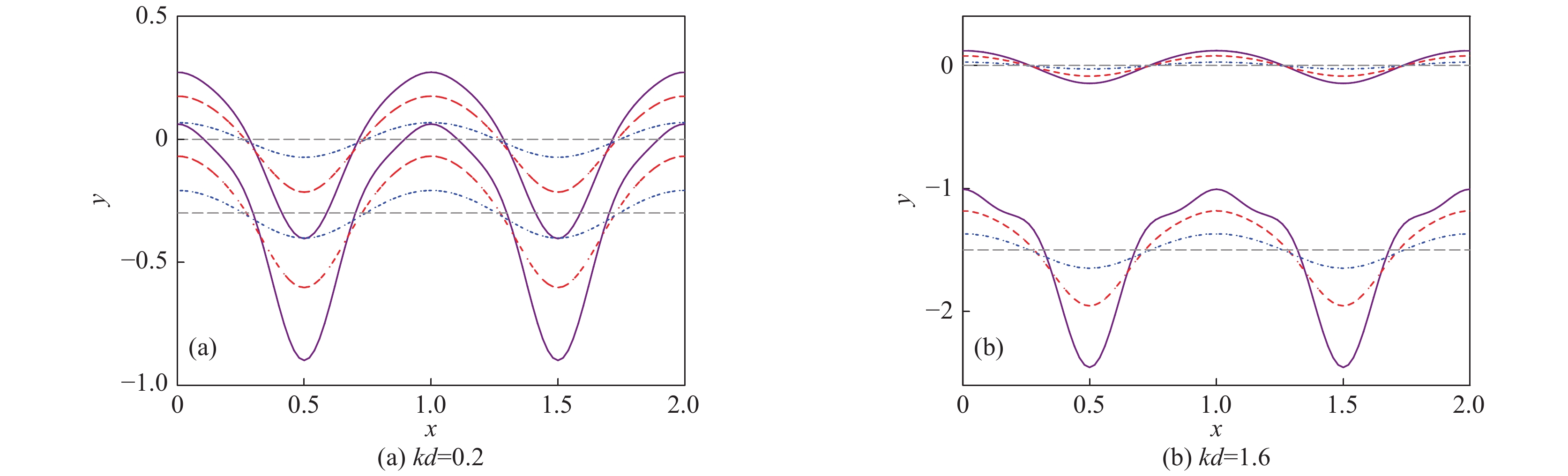
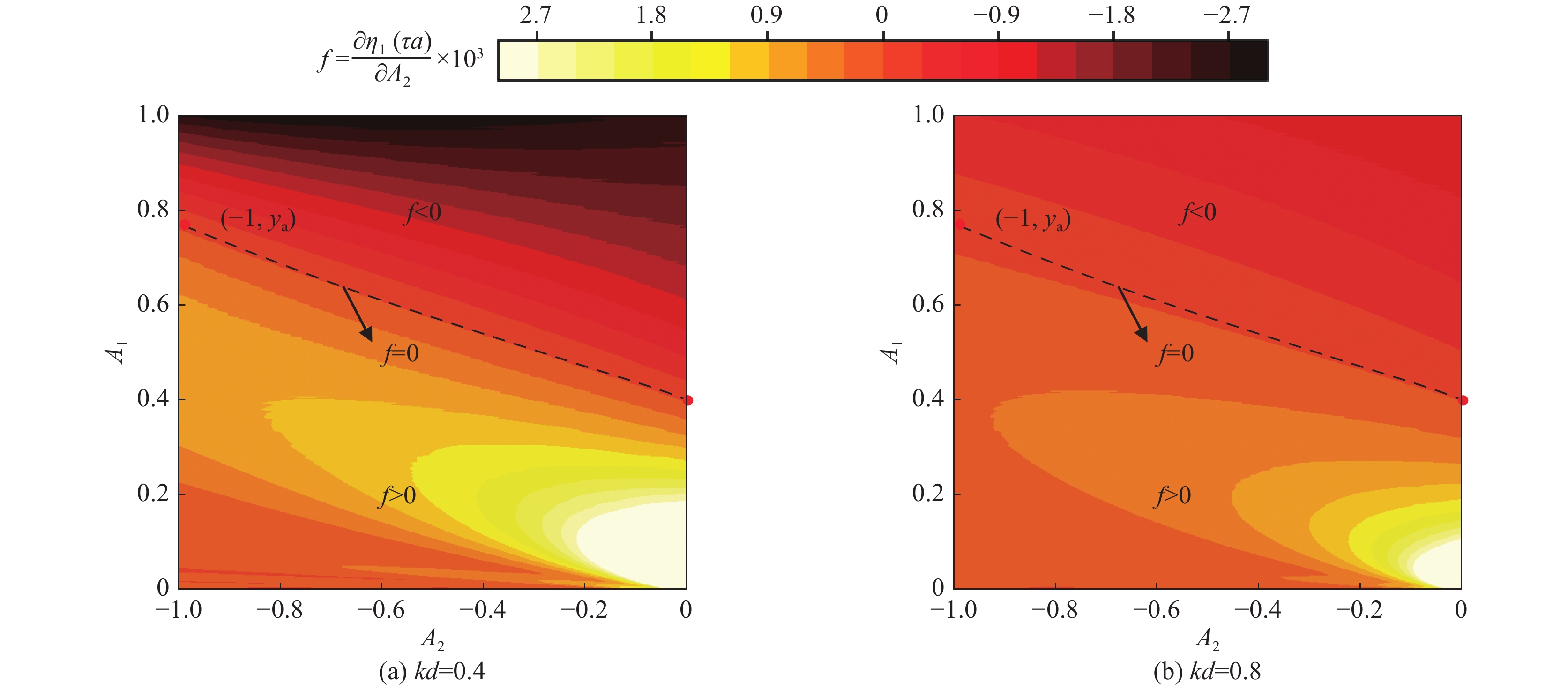
图 55 平面、柱和球几何中内界面扰动振幅和外界面处扰动振幅随时间的演化曲线,初始内界面处的扰动为ηi=0.001λ。扰动模数为l=3,Atwood数为A1=0.9,A2=−0.9
Figure 55. Temporal evolution of f normalized amplitudes of perturbations and initiated by onlythe inner interface perturbation with ηi=0.001λ,the perturbation mode number is l=3,Atwood numbers are A1=0.9 and A2=−0.9
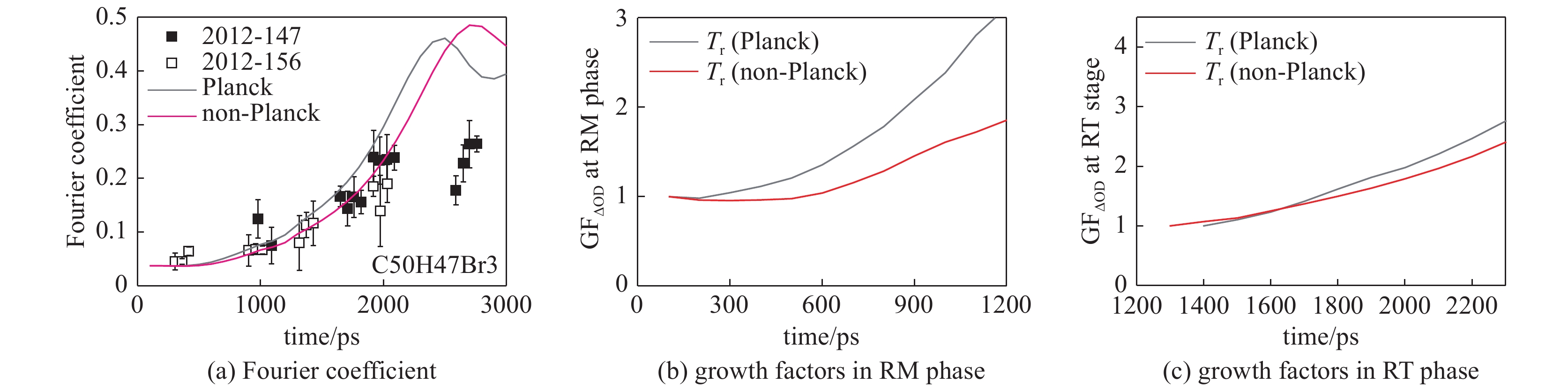
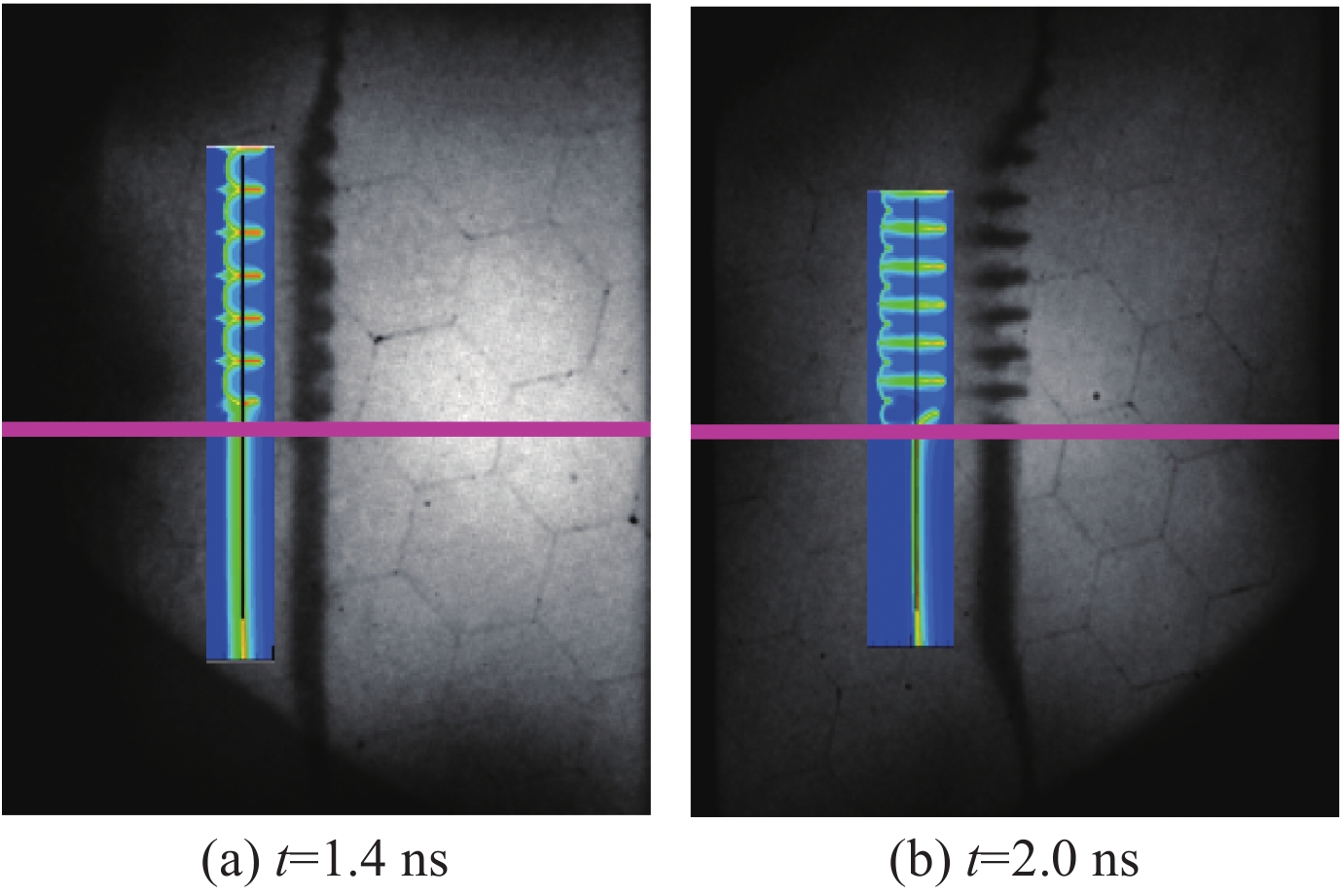
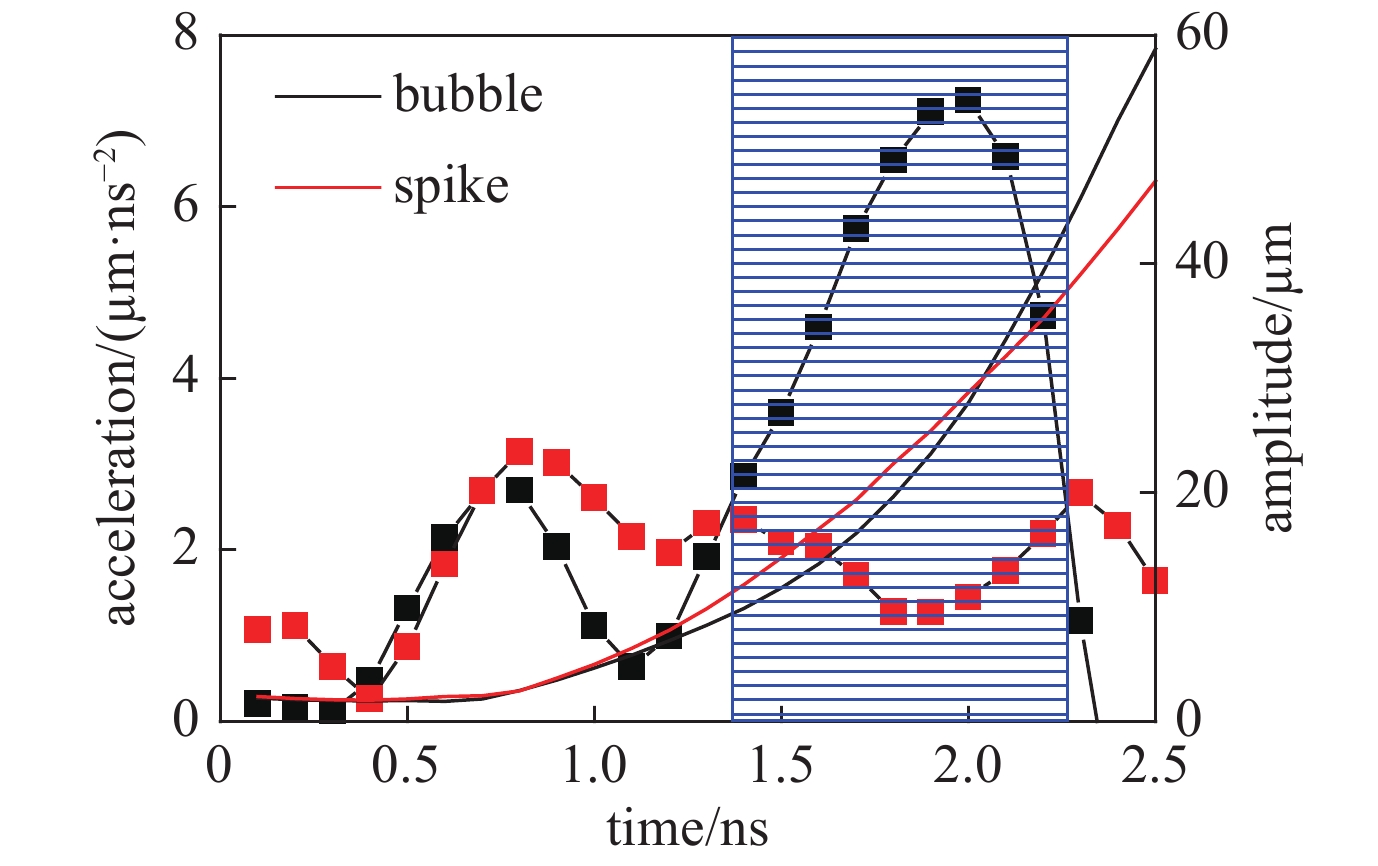
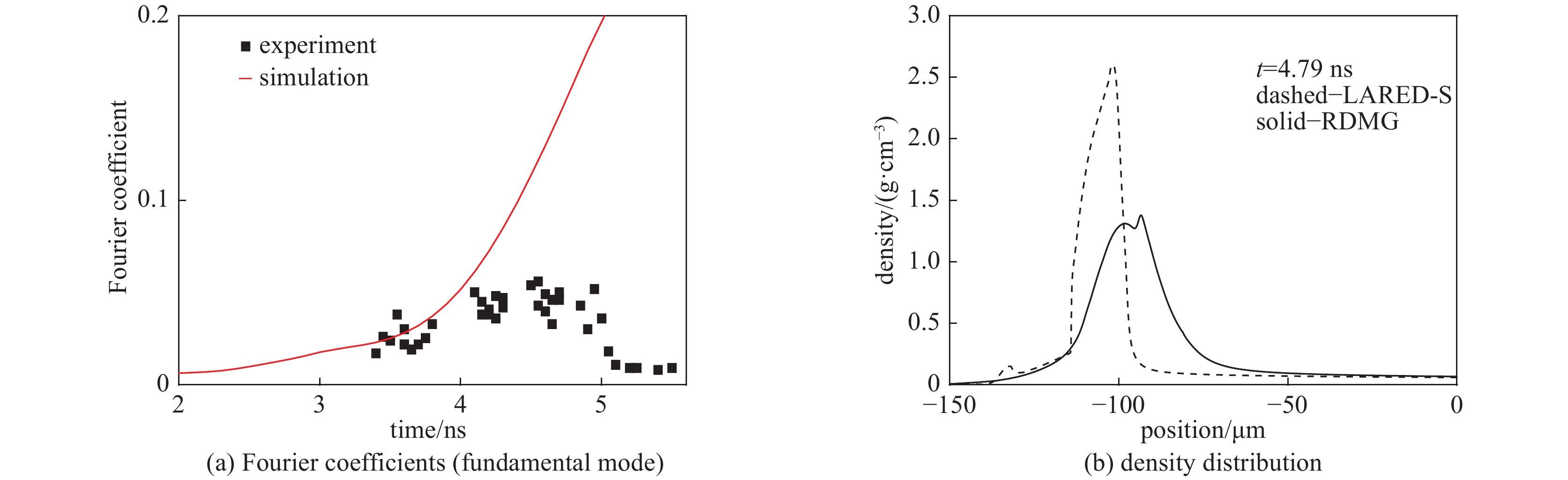
图 73 (a)初始小扰动模拟与实验流体不稳定性增长的比对;(b)RM阶段的增长因子;(c)RT阶段的增长因子
Figure 73. (a) Comparison of the full time dependence of the Fourier coefficient of ΔOD from the experimental measurement and that from the predictions of the LARED-S 2-D hydrodynamic simulations. Temporal evolution of the growth factor of the contrast,GF (∆OD),within the early RM phase (b) and later RT growth stage (c),resulted from numerical simulations adopting the Planckian and non-Planckian spectra,respectively
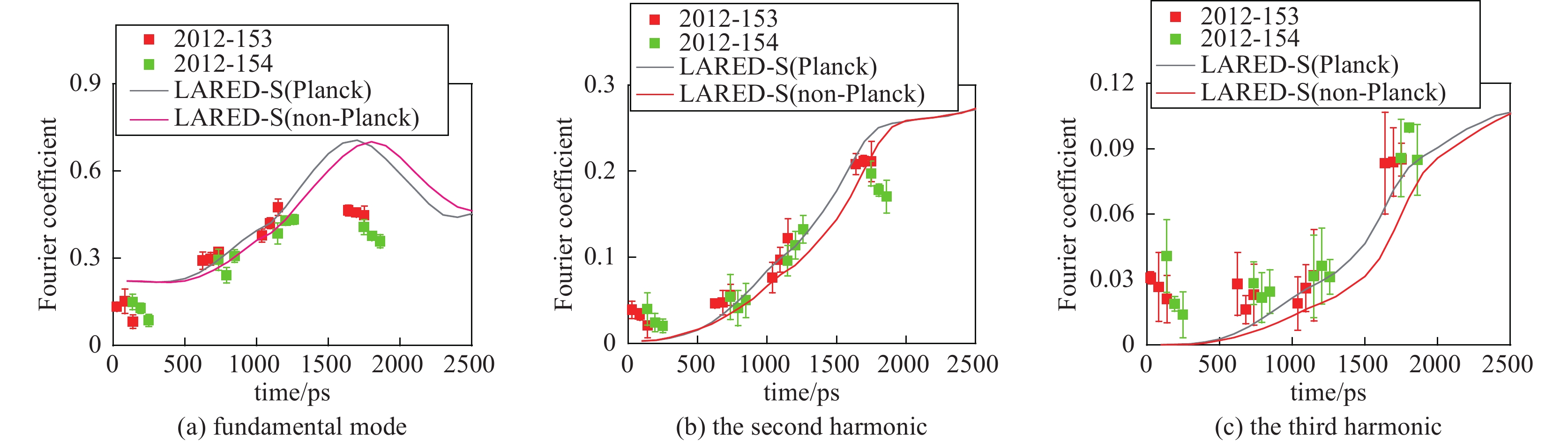
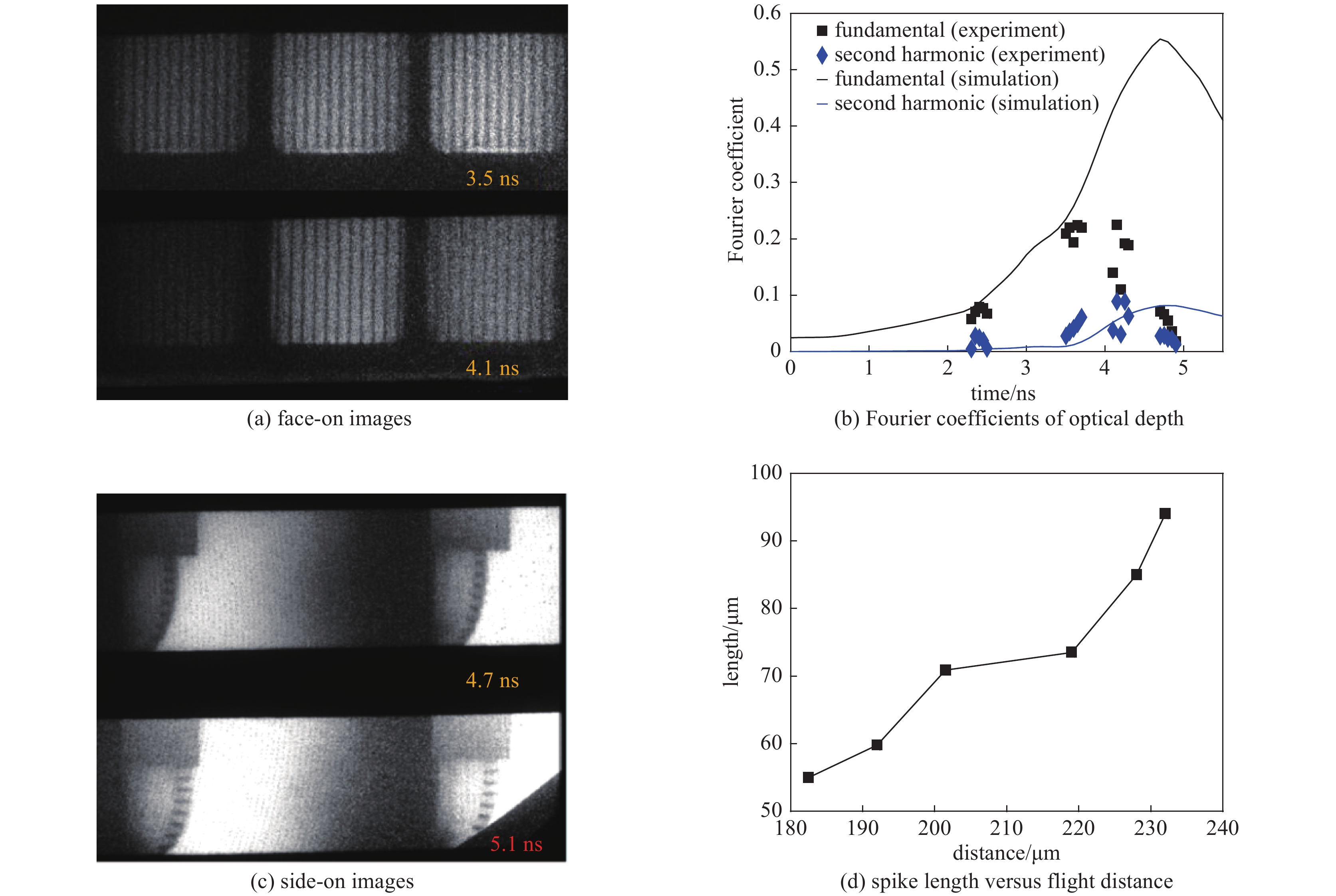
图 74 初始大扰动模拟与实验流体不稳定性增长的比对(a)基模(b)二次谐波(c)三次谐波
Figure 74. Comparison of full time dependence of the first three Fourier coefficients of DOD from experimental data and that from the predictions of the LARED-S 2-D hydrodynamic simulations.(a) Fundamental mode,(b) the second harmonic,and (c) the third harmonic
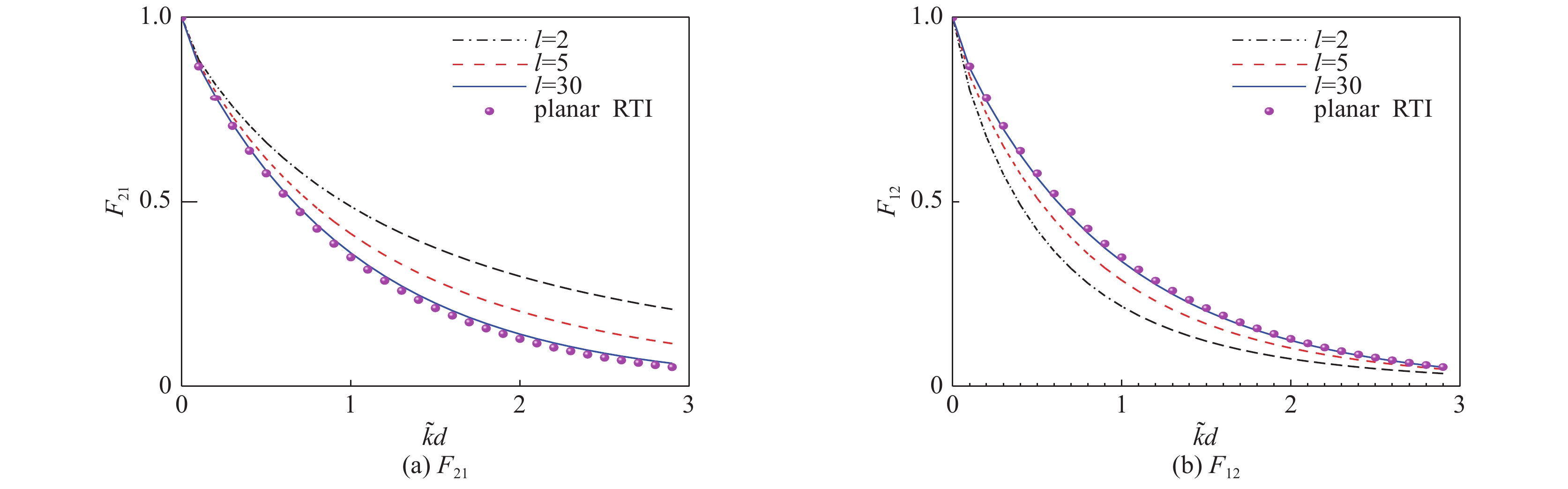
表 1 平面、柱、球几何中的反馈系数
Table 1. Feedthrough coefficients in planar,cylindrical and spherical geometries
feedthrough coefficient (from outer
interface to inner interface)feedthrough coefficients (from inner
interface to outer interface)planar ${{\rm{e}}^{ - kd}}$ ${{\rm{e}}^{ - kd}}$ cylindrical ${\left( {\dfrac{{{R_2}}}{{{R_1}}}} \right)^{ - m + 1}}$ ${\left( {\dfrac{{{R_2}}}{{{R_1}}}} \right)^{ - m{\rm{ - }}1}}$ spherical ${\left( {\dfrac{{{R_2}}}{{{R_1}}}} \right)^{ - l + 1}}$ ${\left( {\dfrac{{{R_2}}}{{{R_1}}}} \right)^{ - l{\rm{ - }}2}}$ 表 2 通过七阶保平衡AWENO-Z-LF计算的
${L^1}$ 误差。Table 2.
${L^1}$ errors computed by the seventh-order AWENO-Z-LF schemeN ρ ρu E 40 2.22×10−15 5.11×10−16 1.56×10−15 200 5.55×10−15 1.08×10−15 1.78×10−15 表 3 通过九阶保平衡AWENO-Z-LF计算的
${L^1}$ 误差。Table 3.
${L^1}$ errors computed by the ninth-order AWENO-Z-LF schemeN ρ ρu E 40 2.22×10−15 1.12×10−15 1.55×10−15 200 4.00×10−15 1.21×10−15 2.22×10−15 -
[1] Committee on High Energy Density Plasma Physics, Plasma Science Committee Board on Physics and Astronomoy Division on Engineering and Physical Science. Frontiers in high energy density physics[M]. Washington D C: The National Academies Press, 2001. [2] Turner M. Connecting quarks with the COSMOS: Eleven science questions for the new century[M]. Washington D C: The National Academies Press, 2003. [3] Remington B A, Drake R P, Ryutov D D. Experimental astrophysics with high power lasers and Z pinches[J]. Rev Mod Phys, 2006, 78: 755-807. doi: 10.1103/RevModPhys.78.755 [4] Drake R P. High-energy-density physics: Fundamentals, Inertial Fusion and Experimental Astrophysics[M]. New York: Springer, 2006. [5] Moses E I. Ignition on the National Ignition Facility: A path towards inertial fusion energy[J]. Nucl Fusion, 2009, 49: 104022. doi: 10.1088/0029-5515/49/10/104022 [6] Lindl J, Landen O, Edwards J, et al. Review of the National Ignition Campaign 2009-2012[J]. Phys Plasmas, 2014, 21: 020501. doi: 10.1063/1.4865400 [7] Hurricane O A, Callahan D A, Casey D T, et al. Inertially confined fusion plasmas dominated by alpha-particle self-heating[J]. Nat Phys, 2016, 12: 800. doi: 10.1038/nphys3720 [8] Hurricane O A, Callahan D A, Springer P T, et al. Beyond alpha-heating: Driving inertially confined fusion implosions toward a burning-plasma state on the National Ignition Facility[J]. Plasma Phys Controlled Fusion, 2019, 61: 014033. doi: 10.1088/1361-6587/aaed71 [9] Hurricane O A, Springer P T, Patel P K, et al. Approaching a burning plasma on the NIF[J]. Phys Plasmas, 2019, 26: 052704. doi: 10.1063/1.5087256 [10] Döppner T, Hinkel D E, Jarrott L C, et al. Achieving 280 Gbar hot spot pressure in DT-layered CH capsule implosions at the National Ignition Facility[J]. PhysPlasmas, 2020, 27: 042701. [11] Boehly T R, Brown D L, Craxton R S, et al. Initial performance results of the OMEGA laser system[J]. Opt Commun, 1997, 133: 495-506. doi: 10.1016/S0030-4018(96)00325-2 [12] Miquel J L, Prene E. LMJ & PETAL status and program overview[J]. Nucl Fusion, 2019, 59: 032005. doi: 10.1088/1741-4326/aac343 [13] Rozanov V, Guskov S Y, Vergunova G A, et al. Direct drive targets for the megajoule installation UFL-2M[R]. J Phys: Conf Ser, 2016, 688: 012095. [14] Yamanaka C, Kato Y, Izama Y, et al. Nd-doped phosphate glass laser systems for laser-fusion research[J]. IEEE J Quantum Electron, 1981, 9: 1639-1649. [15] Lin Z, Deng X, Fan D, et al. SG-Ⅱlaser elementary research and precision SG-Ⅱprogram[J]. Fusion Engineering and Design, 1999, 44: 61-66. doi: 10.1016/S0920-3796(98)00308-1 [16] Deeney C, Douglas M R, Spielman R B, et al. Enhancement of X-ray power from a Z pinch using nested-wire arrays[J]. Phys Rev Lett, 1998, 81: 4883-4886. doi: 10.1103/PhysRevLett.81.4883 [17] Jones M C, Ampleford D J, Cuneo M E, et al. X-ray power and yield measurements at the refurbished Z machine[J]. Rev Sci Instrum, 2014, 85: 083501. doi: 10.1063/1.4891316 [18] Deng J J, Xie W P, Feng S P, et al. From concept to reality – A review to the primary test stand and its preliminary application in high energy density physics[J]. Matter and Radiation at Extremes, 2016, 1: 48-58. doi: 10.1016/j.mre.2016.01.004 [19] 温树槐, 丁永坤. 激光惯性约束聚变诊断学[M]. 北京: 国防工业出版社, 2012.Wen Shuhuai, Ding Yongkun. Laser inertial confinement fusion diagnostics[M].Beijing: National Defense Industry Press, 2012. [20] 江少恩, 丁永坤, 缪文勇, 等. 我国激光惯性约束聚变实验研究进展[J]. 中国科学: 物理力学天文学, 2009, 39(11):1571-1583. (Jiang Shaoen, Ding Yongkun, Miao Wenyong, et al. Recent progress of inertial confinement fusion experiments in China[J]. Sci China Phys Mech Astron, 2009, 39(11): 1571-1583 [21] 王峰, 江少恩. 神光装置实验和诊断技术进展专题·编者按[J]. 中国科学: 物理学力学天文学, 2018, 48:065201. (Wang Feng, Jiang Shaoen. Special topic: Progress of experimental and diagnostical technique based on Shenguang series laser facility[J]. Sci China Phys Mech Astron, 2018, 48: 065201 doi: 10.1360/SSPMA2018-00095 [22] Zimmerman G, Kershaw D, Bailey D, et al. The Lasnex code for inertial confinement fusion[R]. UCRL-80169, 1977. [23] Stone G F, Spragge M R, Rivers C J, et al. Fabrication and testing of gas-filled targets for large-scale plama experiments on NOVA[R]. UCRL-LR-105821-95-3, 1995. [24] Radha P B, Goncharov V N, Collins T J B, et al. Two-dimensional simulations of plastic-shell, direct-drive implosions on OMEGA[J]. Phys Plasmas, 2005, 12: 032702. doi: 10.1063/1.1857530 [25] He X T, Zhang W Y. Inertial fusion research in China[J]. Eur Phys J D, 2007, 44: 227-231. doi: 10.1140/epjd/e2007-00005-1 [26] Pei Wenbing. The construction of simulation algorithms for laser fusion[J]. Commun Comput Phys, 2007, 2: 255-270. [27] Rayleigh L. Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density[J]. Nature, 1883, 14: 170-177. [28] Taylor G. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes[J]. I Proc R Soc London A, 1950, 201: 192-196. doi: 10.1098/rspa.1950.0052 [29] Richtmyer D. Taylor instability in shock acceleration of compressible fluids[J]. Comm Pure Appl Math, 1960, 13: 297-319. doi: 10.1002/cpa.3160130207 [30] Meshkov E E. Instability of the interface of two gases accelerated by a shock wave[J]. Fluid Dynam, 1969, 4: 101-108. [31] Kelvin L. Hydrokinetic solutions and observations, on the motion of free solids through a liquid, mathematical and physical papers IV[M]. Cambridge: Hydrodynamics and General Dynamics, 1910. [32] Von Helmholtz H. On the discontinuous movements of fluids[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1868, 36: 337-346. doi: 10.1080/14786446808640073 [33] Bell G I. Taylor instability on cylinders and spheres in the small amplitude approximation[R]. LA-1321, 1951. [34] Plesset M S. On the stability of fluid flows with spherical symmetry[J]. J Appl Phys, 1954, 25: 96-98. doi: 10.1063/1.1721529 [35] Chandrasekhar S. Hydrodynamic and hydromagnetic stability[M]. London: Oxford University, 1961. [36] Drazin P G, Reid W H. Hydrodynamic stability[M]. Cambridge: Cambridge University Press, 2004. [37] Bateman G. Magnetohydrodynamic instability[M]. Beijing: Atomic Energy Press, 1982. [38] Ma T, Patel P K, Izumi N, et al. Onset of hydrodynamic mix in high-velocity, highly compressed inertial confinement fusion implosions[J]. Phys Rev Lett, 2013, 111: 085004. doi: 10.1103/PhysRevLett.111.085004 [39] Edwards M J, Patel P K, Lindl J D, et al. Progress towards ignition on the National Ignition Facility[J]. Phys Plasmas, 2013, 20: 070501. doi: 10.1063/1.4816115 [40] Ma T, Hurricane O A, Callahan D A, et al. Thin shell, high velocity inertial confinement fusion implosions on the National Ignition Facility[J]. Phys Rev Lett, 2015, 114: 145004. doi: 10.1103/PhysRevLett.114.145004 [41] Remington B, Arnett D, Drake P, et al. Modeling astrophysical phenomena in the laboratory with intense lasers[J]. Science, 1999, 284: 1488-1493. doi: 10.1126/science.284.5419.1488 [42] 李宗伟, 肖兴华. 天体物理学[M]. 北京: 高等教育出版社, 2001.Li Zongwei, Xiao Xinghua. Astrophysics[M]. Beijing: Higher Education Press, 2001 [43] 黄润乾. 恒星物理[M]. 北京: 中国科学出版社, 1998.Huang Runqian. Stellar Physics[M]. Science Press, 1998. [44] 王贻仁, 张锁春, 谢佐恒, 等. 超新星爆发机制和数值模拟[M]. 郑州: 河南科学技术出版社, 2003.Wang Yiren, Zhang Shuochun, Xie Zuoheng. Supernova explosion mechanism and numerical simulation[M]. Zhengzhou: Henan Science and Technology Press, 2003 [45] 徐仁新. 天体物理学导论[M]. 北京: 北京大学出版社, 2006.Xu Renxin. Introduction to astrophysics[M]. Beijing: Peking University Press, 2006. [46] Nomoto K, Yamaoka H, Pols O R, et al. A carbon–oxygen star as progenitor of the type Ic supernova 1994I[J]. Nature, 1994, 371: 227-229. doi: 10.1038/371227a0 [47] Kouveliotou C. Gamma ray bursts[J]. Science, 1997, 277: 1257-1258. doi: 10.1126/science.277.5330.1257 [48] Baron E. How big do stellar explosions get?[J]. Nature, 1998, 395: 635-636. doi: 10.1038/27067 [49] Iwamoto K, Mazzali P A, Nomoto K, et al. A hypernova model for the supernova associated with the γ-ray burst of 25 April 1998[J]. Nature, 1998, 395: 672-674. doi: 10.1038/27155 [50] Hasegawa H, Fujimoto M, Phan T-D, et al. Transport of solar wind into Earth's magnetosphere through rolled-up Kelvin-Helmholtz vortices[J]. Nature, 2004, 430: 755-758. doi: 10.1038/nature02799 [51] Gamezo V N, Khokholv A M, Oran E S, et al. Thermonuclear supernovae: simulations of the deflagration stage and their implications[J]. Science, 2003, 299: 77-80. doi: 10.1126/science.1078129 [52] Dimonte G, Youngs D L, Dimits A, et al. A comparative study of the turbulent Rayleigh-Taylor instability using high-resolution three-dimensional numerical simulations: The Alpha-Group collaboration[J]. Phys Fluids, 2004, 16(5): 1668-1693. doi: 10.1063/1.1688328 [53] Zhou Y, Remington B A, Robey H F, et al. Progress in understanding turbulent mixing induced by Rayleigh–Taylor and Richtmyer–Meshkov instabilities[J]. Phy Plasmas, 2003, 10(5): 1883-1896. doi: 10.1063/1.1560923 [54] Zhou Y, Clark T T, Clark D S, et al. Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities[J]. Phys Plasmas, 2019, 26: 080901. doi: 10.1063/1.5088745 [55] Marinak M M, Tipton R E, Landen O L, et al. Three-dimensional simulations of Nova high growth factor capsule implosion experiments[J]. Phys Plasmas, 1996, 3(5): 2070-2076. doi: 10.1063/1.872004 [56] Clark D S, Weber C R, Milovich J L, et al. Three-dimensional simulations of low foot and high foot implosion experiments on the National Ignition Facility[J]. Phys Plasmas, 2016, 23: 056302. doi: 10.1063/1.4943527 [57] Clark D S, Weber C R, Milovich J L, et al. Three-dimensional modeling and hydrodynamic scaling of National Ignition Facility implosions[J]. Phys Plasmas, 2019, 26: 050601. doi: 10.1063/1.5091449 [58] Clark D S, Weber C R, Kritcher A L, et al. Modeling and projecting implosion performance for the National Ignition Facility[J]. Nucl Fusion, 2019, 59: 032008. doi: 10.1088/1741-4326/aabcf7 [59] Weber C R, Clark D S, Cook A W, et al. Three-dimensional hydrodynamics of the deceleration stage in inertial confinement fusion[J]. Phys Plasmas, 2015, 22: 032702. doi: 10.1063/1.4914157 [60] Weber C R, Clark D S, Cook A W, et al. Inhibition of turbulence in inertial-confinement-fusion hot spots by viscous dissipation[J]. Phys Rev E, 2014, 89: 053106. doi: 10.1103/PhysRevE.89.053106 [61] Taylor S, Chittenden J P. Effects of perturbations and radial profiles on ignition of inertial confinement fusion hotspots[J]. Phys Plasmas, 2014, 21: 062701. doi: 10.1063/1.4879020 [62] Chittenden J P, Appelbe B D, Manke F, et al. Signatures of asymmetry in neutron spectra and images predicted by three-dimensional radiation hydrodynamics simulations of indirect drive implosions[J]. Phys Plasmas, 2016, 23: 052708. doi: 10.1063/1.4949523 [63] Woo K M, Betti R, Shvarts D, et al. Effects of residual kinetic energy on yield degradation and ion temperature asymmetries in inertial confinement fusion implosions[J]. Phys Plasmas, 2018, 25: 052704. doi: 10.1063/1.5026706 [64] Haines B M, Grinstein F F, Fincke J R. Three-dimensional simulation strategy to determine the effects of turbulent mixing on inertial-confinement-fusion capsule performance[J]. Phy Rev E, 2014, 89: 053302. doi: 10.1103/PhysRevE.89.053302 [65] Haines B M, Olson R E, Sweet W, et al. Robustness to hydrodynamic instabilities in indirectly driven layered capsule implosions[J]. Phys Plasmas, 2019, 26: 012707. doi: 10.1063/1.5080262 [66] 张维岩, 叶文华, 吴俊峰, 等. 激光间接驱动聚变内爆流体不稳定性研究[J]. 中国科学: 物理学力学天文学, 2014, 44:1-23. (Zhang Weiyan, Ye Wenhua, Wu Junfeng, et al. Hydrodynamic instabilities of laser indirect-drive inertial-confinement-fusion implosion[J]. Sci Sin-Phys Mech Astron, 2014, 44: 1-23 doi: 10.1360/SSPMA2013-00039 [67] Wang L F, Ye W H, He X T, et al. Theoretical and simulation research of hydrodynamic instabilities in inertial-confinement fusion implosions[J]. Sci China-Phys Mech Astron, 2017, 60: 055201. doi: 10.1007/s11433-017-9016-x [68] Casner A, Masse L, Delorme B, et al. Progress in indirect and direct-drive planar experiments on hydrodynamic instabilities at the ablation front[J]. Phys Plasmas, 2014, 21: 122702. doi: 10.1063/1.4903331 [69] Mailliet C, Bel E L, Ceurvorst L, et al. Long-duration direct drive hydrodynamics experiments on the National Ignition Facility: Platform development and numerical modeling with CHIC[J]. Phys Plasmas, 2019, 26: 082703. doi: 10.1063/1.5110684 [70] Kline J L. Deconstructing integrated high energy density physics experiments into fundamental models for validatioin[R]. LA-UR-19-20544, 2019. [71] Doss F W, LoomisE N, Welser-Sherrill L, et al. Instability, mixing, and transition to turbulence in a laser-driven counterflowing shear experiment[J]. Phys Plasmas, 2013, 20: 012707. doi: 10.1063/1.4789618 [72] Flippo K A, Kline J L, Doss F W, et al. Development of a big area back lighter for high energy density experiments[J]. Rev Sci Inst, 2014, 85: 093501. doi: 10.1063/1.4893349 [73] Robey H F, Miles A R, Hansen J F, et al. Laser-driven hydrodynamic experiments in the turbulent plasma regime: From Omega to NIF[R]. UCRL-JC-I 55300, 2003. [74] Blue B E, Weber S V, Glendinning S G, et al. Experimental investigation of high-Mach-number 3D hydrodynamic jets at the National Ignition Facility[J]. Phys Rev Lett, 2005, 94: 095005. doi: 10.1103/PhysRevLett.94.095005 [75] Lanier N E, Barnes C W, Batha S H, et al. Multimode seeded Richtmyer–Meshkov mixing in a convergent, compressible, miscible plasma system[J]. Phys Plasmas, 2003, 10(5): 1816-1821. doi: 10.1063/1.1542886 [76] Pomraning G C. The equations of radiation hydrodynamics[M]. Oxford: Pergamon Press, 1973. [77] Mihalas D, Mihalas B W. Foundations of radiation hydrodynamics[M]. Oxford: Oxford University Press, 1984. [78] Castor J I. Radiation hydrodynamics[M]. Cambridge: Cambridge University Press, 2004. [79] Toro E F. Riemann solvers and numerical methods for fluid dynamics[M]. Berlin: Springer, 1997. [80] Hirt C W, Amsden AA, Cook J L. An arbitrary Lagrangian-Eulerian computing method for all flow speeds[J]. J Comput Phys, 1974, 14: 227-253. doi: 10.1016/0021-9991(74)90051-5 [81] Berger M, Oliger J. Adaptive mesh refinement for hyperbolic partial differential equations[J]. J Comput Phys, 1984, 53: 484-512. doi: 10.1016/0021-9991(84)90073-1 [82] 叶文华, 张维岩, 陈光南. 激光烧蚀瑞利-泰勒不稳定性模拟[J]. 强激光与粒子束, 1998, 10(3):403-408. (Ye Wenhua, Zhang Weiyan, Cheng Guangnan. Numerical simulation of laser ablative Rayleigh-Taylor instability[J]. High Power Laser and Particle Beams, 1998, 10(3): 403-408 [83] Ye W H, Zhang W Y, He X T. Stabilization of ablative Rayleigh-Taylor instability due to change of the Atwood number[J]. Phys Rev E, 2002, 65: 057401. doi: 10.1103/PhysRevE.65.057401 [84] 吴俊峰. 收缩几何中惯性约束聚变流体不稳定性的理论和数值模拟研究[D]. 北京: 中国工程物理研究院, 2003..Wu Junfeng. Theoretic and numerical studies on hydrodynamic instabilities of flows in inertial confined fusion under convergent geometry[D]. Beijing: China Academy of Engineering Physics, 2003 [85] 郁晓瑾, 叶文华, 吴俊峰. 直接驱动内爆点火的数值模拟研究[J]. 强激光与粒子束, 2006, 18(8):1297-1301. (Yu Xiaojin, Ye Wenhua, Wu Junfeng. Numerical simulation of direct-drive ICF ignition in spherical geometry[J]. High Power Laser and Particle Beams, 2006, 18(8): 1297-1301 [86] 郁晓瑾, 吴俊峰, 叶文华. 激光非均匀性对内界面变形影响的研究[J]. 强激光与粒子束, 2007, 19(8):1283-1286. (Yu Xiaojin, Wu Junfeng, Ye Wenhua. Numerical simulation of effect of laser nonuniformity on interior interface[J]. High Power Laser and Particle Beams, 2007, 19(8): 1283-1286 [87] Wang L F, Xue C, Ye W H, et al. Destabilizing effect of density gradient on the Kelvin-Helmholtz instability[J]. Phys Plasmas, 2009, 16: 112104. doi: 10.1063/1.3255622 [88] Wang L F, Ye W H, Sheng Z M, et al. Preheating ablation effects on the Rayleigh-Taylor instability in the weakly nonlinear regime[J]. Phys Plasmas, 2010, 17: 122706. doi: 10.1063/1.3517606 [89] Wang L F, Ye W H, Don W S, et al. Formation of large-scale structures in the ablative Kelvin-Helmholtz instability[J]. Phys Plasmas, 2010, 17: 122308. doi: 10.1063/1.3524550 [90] Wang L F, Ye W H, He X T, et al. Formation of jet-like spikes from the ablative Rayleigh-Taylor instability[J]. Phys Plasmas, 2012, 19: 100701. doi: 10.1063/1.4759161 [91] Fan Z, Zhu S, Pei W, et al. Numerical investigation on the stabilization of the deceleration phase Rayleigh-Taylor instability due to alpha particle heating in ignition target[J]. EPL, 2012, 99: 65003. doi: 10.1209/0295-5075/99/65003 [92] Fan Z F, He X T, Liu J, et al. A wedged-peak-pulse design with medium fuel adiabat for indirect-drive fusion[J]. Phys Plasmas, 2014, 21: 100705. doi: 10.1063/1.4898682 [93] Wang L F, Ye W H, Wu J F, et al. Main drive optimization of a high-foot pulse shape in inertial confinement fusion implosions[J]. Phys Plasmas, 2016, 23: 122702. doi: 10.1063/1.4971237 [94] Wang L F, Ye W H, Wu J F, et al. A scheme for reducing deceleration-phase Rayleigh-Taylor growth in inertial confinement fusion implosions[J]. Phys Plasmas, 2016, 23: 052713. doi: 10.1063/1.4952636 [95] He X T, Li J W, Fan Z F, et al. A hybrid-drive nonisobaric-ignition scheme for inertial confinement fusion[J]. Phys Plasmas, 2016, 23: 082706. doi: 10.1063/1.4960973 [96] Fan Z F, Liu Y Y, Liu B, et al. Non-equilibrium between ions and electrons inside hot spots from National Ignition Facility experiments[J]. Matter and Radiat Extrem, 2017, 2: 3-8. doi: 10.1016/j.mre.2016.11.003 [97] Mo Zeyao, Zhang Aiqing, Cao Xiaolin, et al. JASMIN: A parallel software infrastructure for scientific computing[J]. Front Comput Sci China, 2010, 4(4): 480-488. [98] 刘青凯, 徐小文, 吴俊峰. 一种求解流体力学方程组的自适应显式时间积分算法及其应用[J]. 计算物理, 2011, 28(2):174-180. (Liu Qingkai, Xu Xiaowen, Wu Junfeng. An adaptive explicit time integration algorithm for hydrodynamic equations and application in ICF[J]. Chinese Journal of Computational Physics, 2011, 28(2): 174-180 [99] 徐小文, 莫则尧, 刘青凯,等. 自适应结构网格上扩散方程隐式时间积分算法及应用[J]. 计算物理, 2012, 29(5):684-692. (Xu Xiaowen, Mo Zeyao, Liu Qingkai, et al. An implicit time-integration algorithm for diffusion equations with structured AMR and applications[J]. Chinese Journal of Computational Physics, 2012, 29(5): 684-692 [100] 莫则尧, 张爱清, 曹小林, 等. 多介质辐射流体力学数值模拟中的并行计算研究[J]. 自然科学进展, 2006, 16(3):287-292. (Mo Zeyao, Zhang Aiqing, Cao Xiaolin, et al. Research on parallel computing in numerical simulation of multi-media radiation hydrodynamics[J]. Progress in Natural Science, 2006, 16(3): 287-292 [101] 裴文兵, 朱少平. 激光聚变中的科学计算[J]. 物理, 2009, 38(8):559-568. (Pei Wenbing, Zhu Shaoping. Scientific calculation in laser fusion[J]. Physics, 2009, 38(8): 559-568 [102] Marvin L A. Subcell balance methods for radiative transfer on arbitrary grids[J]. Transport Theory and Statistical Physics, 1997, 26(4/5): 285-431. [103] Morel J E. Diffusion-limit asymptotics of the transport equation, the P1/3 equations, and two flux-limited diffusion theories[J]. J Qunat Spectrosc Radiat Transfer, 2000, 5(65): 769-778. [104] 袁光伟, 杭旭登, 盛志强, 等. 辐射扩散计算方法若干研究进展[J]. 计算物理, 2009, 26(4):475-500. (Yuan Guangwei, Hang Xudeng, Sheng Zhiqiang, te al. Progress in numerical methods for radiation diffusion equations[J]. Chinese Journal of Computational Physics, 2009, 26(4): 475-500 doi: 10.3969/j.issn.1001-246X.2009.04.001 [105] Saad Y. Iterative methods for sparse linear systems[M]. 2nd ed. Philadelphia: Society for Industrial and Applied Mathematics, 2003. [106] Baldwin C, Brown P N, Falgout R D, et al. Iterative linear solvers in a 2D radiation-hydrodynamics code: Methods and performance[J]. J Comput Phys, 1999, 154: 1-40. [107] Yue Xiaoqiang, Xu Xiaowen, Shu Shi. JASMIN-based adaptive combined preconditioner for 2D radiation diffusion equations in ICF applications[J]. East Asian Journal on Applied Mathematics, 2017, 7(3): 495-507. [108] Xu Xiaowen, Mo Zeyao. Algebraic interface based coarsening AMG preconditioner for multi-scale sparse matrices with applications to radiation hydrodynamics computation[J]. Numer Linear Algebra Appl, 2017, 24(2): e2078. [109] Basov N G, Krokhin O N. Proceeding of the 3rd International Conference on Quantum Electronic[M]. New York: Columbia University Press, 1964. [110] Dawson J M. On the production of plasma by giant pulse lasers[J]. Phys Fluid, 1964, 7: 981-987. doi: 10.1063/1.1711346 [111] 王淦昌. 利用大能量大功率的光激射器产生中子的建议[J]. 原子能科学技术, 1988, 22(1):7. (Wang Ganchang. A proposal of using high energy and high power laser to produce neutrons[J]. Atomic Energy Sci Tech, 1988, 22(1): 7 [112] Nuckolls J, Wood L, Thiessen A, et al. Laser compression of matter to super-high densities: Thermonuclear (CTR) applications[J]. Nature, 1972, 239: 139-142. doi: 10.1038/239139a0 [113] Atzeni S, Meyer-ter-Vehn J. The physics of inertial fusion: Beam plasma interaction hydrodynamics, hot dense matter[M]. Oxford: Oxford University, 2004. [114] 张钧, 常铁强. 激光聚变靶物理基础[M]. 北京: 国防工业出版社, 2004.Zhang Jun, Chang Tieqiang. Fundaments of the target physics for laser fusion[M]. Beijing: National Defense Industry Press, 2004. [115] Kilkenny J D. Experimental results on hydrodynamic instabilities in laser-accelerated planar packages[J]. Phys Fluids B: Plasma Physics, 1990, 2: 1400-1404. doi: 10.1063/1.859563 [116] Remington B A, Weber S V, Haan S W, et al. Laser-driven hydrodynamic instability experiments[J]. Phys Fluids B: Plasma Physics, 1993, 5: 2589-2595. doi: 10.1063/1.860695 [117] Remington B A, Weber S V, Marinak M M, et al. Single-mode and multimode Rayleigh-Taylor experiments on Nova[J]. Phys Plasms, 1995, 2: 241-255. doi: 10.1063/1.871096 [118] Marinak M M, Remington B A, Weber S V, et al. Three-dimensional single mode Rayleigh-Taylor experiments on Nova[J]. Phys Rev Lett, 1995, 75: 3677-3680. doi: 10.1103/PhysRevLett.75.3677 [119] Hsing W W, Hoffman N M. Measurement of feedthrough and instability growth in radiation-driven cylindrical implosions[J]. Phys Rev Lett, 1997, 78: 3876-3879. doi: 10.1103/PhysRevLett.78.3876 [120] Glendinning S G, Colvin J, Haan S W, et al. Ablation front Rayleigh–Taylor growth experiments in spherically convergent geometry[J]. Phys Plasms, 2000, 7: 2033-2039. doi: 10.1063/1.874024 [121] Bradley D K, Braun D G, Glendinning S G, et al. Very-high-growth-factor planar ablative Rayleigh-Taylor experiments[J]. PhysPlasmas, 2007, 14: 056313. [122] Smalyuk V A, Hu S X, Goncharov V N, et al. Systematic study of Rayleigh-Taylor growth in directly driven plastic targets in a laser-intensity range from ~2×1014 to 1.5×1015 W/cm2[J]. Phys Plasmas, 2008, 15: 082703. doi: 10.1063/1.2967899 [123] Sadot O, Smalyuk V A, Delettrez A, et al. Observation of self-similar behavior of the 3D, nonlinear Rayleigh-Taylor instability[J]. Phys Rev Lett, 2005, 95: 265001. doi: 10.1103/PhysRevLett.95.265001 [124] Loomis E N, Braun D, Batha S H, et al. Areal density evolution of isolated surface perturbations at the onset of X-ray ablation Richtmyer-Meshkov growth[J]. Phys Plasmas, 2011, 18: 092702. doi: 10.1063/1.3632083 [125] Desjardins T R, Di Stefanob C A, Day T, et al. A platform for thin-layer Richtmyer-Meshkov at OMEGA and the NIF[J]. High Energy Density Physics, 2019, 33: 100705. doi: 10.1016/j.hedp.2019.100705 [126] Smalyuk V A, Delettrez J A, Goncharov V N, et al. Rayleigh-Taylor instability in the deceleration phase of spherical implosion experiments[J]. Phys Plasmas, 2002, 9: 2738-2744. doi: 10.1063/1.1476308 [127] Smalyuk V A, Hu S X, Hager J D, et al. Rayleigh-Taylor growth measurements in the acceleration phase of spherical implosions on OMEGA[J]. Phys Rev Lett, 2009, 103: 105001. [128] Parker K, Horsfield C J, Rothman S D, et al. Observation and simulation of plasma mix after reshock in a convergent geometry[J]. Phys Plasmas, 2004, 11: 2696-2701. doi: 10.1063/1.1647131 [129] Rinderknecht H G, Sio H, Li C K, et al. First observations of nonhydrodynamic mix at the fuel-shell interface in shock-driven inertial confinement implosions[J]. Phys Rev Lett, 2014, 112: 135001. doi: 10.1103/PhysRevLett.112.135001 [130] Casner A, Galmiche D, Huser G, et al. Indirect drive ablative Rayleight-Taylor experiments with rugby hohlraums on OMEGA[J]. Phys Plasmas, 2009, 16: 092701. doi: 10.1063/1.3224027 [131] Ali S J, Celliers P M, Haan S W, et al. Hydrodynamic instability seeding by oxygen nonuniformities in glow discharge polymer inertial fusion ablators[J]. Phys Rev E, 2018, 98: 033204. doi: 10.1103/PhysRevE.98.033204 [132] Ali S J, Celliers P M, Haan S, et al. Probing the seeding of hydrodynamic instabilities from nonuniformities in ablator materials using 2D velocimetry[J]. Phys Plasmas, 2018, 25: 092708. doi: 10.1063/1.5047943 [133] Aglitskiy Y, Velikovich A L, Karasik M, et al. Basic hydrodynamics of Richtmyer-Meshkov-type growth and oscillations in the inertial confinement fusion-relevant conditions[J]. Phil TransR Soc A, 2010, 368: 1739-1768. doi: 10.1098/rsta.2009.0131 [134] Metzler N, Velikovich A L, Schmitt A J, et al. Laser imprint reduction with a shaping pulse, oscillatory Richtmyer-Meshkov to Rayleigh-Taylor transition and other coherent effects in plastic-foam targets[J]. Phys Plasmas, 2003, 10: 1897-1905. doi: 10.1063/1.1560616 [135] Aglitskiy Y, Karasik M, Velikovich A L, et al. Observed transition from Richtmyer-Meshkov jet formation through feedout oscillations to Rayleigh-Taylor instability in a laser target[J]. Phys Plasmas, 2012, 19: 102707. doi: 10.1063/1.4764287 [136] Smalyuk V A, Weber C R, Landen O L, et al. Review of hydrodynamic instability experiments in inertially confined fusion implosions on National Ignition Facility[J]. Plasma Phys Control Fusion, 2020, 62: 014007. doi: 10.1088/1361-6587/ab49f4 [137] Smalyuk V A, Tipton R E, Pino J E, et al. Measurements of an ablator-gas atomic mix in indirectly driven implosions at the National Ignition Facility[J]. Phys Rev Lett, 2014, 112: 025002. doi: 10.1103/PhysRevLett.112.025002 [138] Martinez D A, Smalyuk V A, Kane J O, et al. Evidence for a bubble-competition regime in indirectly driven ablative Rayleigh-Taylor instability experiments on the NIF[J]. Phys Rev Lett, 2015, 114: 215004. doi: 10.1103/PhysRevLett.114.215004 [139] Casner A, Mailliet C, Khan S F, et al. Long-duration planar direct-drive hydrodynamics experiments on the NIF[J]. Plasma Physics and Controlled Fusion, 2018, 60: 014012. doi: 10.1088/1361-6587/aa8af4 [140] Nagel S R, Raman K S, Huntington C M, et al. A platform for studying the Rayleigh-Taylor and Richtmyer-Meshkov instabilities in a planar geometry at high energy density at the National Ignition Facility[J]. Phys Plasmas, 2017, 24: 072704. doi: 10.1063/1.4985312 [141] Fujioka S, Shiraga H, Nishikino M, et al. First observation of density profile in directly laser-driven polystyrene targets for ablative Rayleigh-Taylor instability research[J]. Phys Plasmas, 2003, 10: 4784-4789. doi: 10.1063/1.1622951 [142] Shigemori K, Azechi H, Fujioka S, et al. Hydrodynamic instability experiments on the HIPER laser[J]. AIP Conference Proceedings, 2003, 669: 269-272. doi: 10.1063/1.1593917 [143] Otani K, Shigemori K, Sakaiya T, et al. Reduction of the Rayleigh-Taylor instability growth with cocktail color irradiation[J]. Phys Plasmas, 2007, 14: 122702. doi: 10.1063/1.2817092 [144] Endo T, Shigemori K, Azechi H, et. al Dynamic behavior of rippled shock waves and subsequently induced areal-density-perturbation growth in laser-irradiated foils[J]. Phys Rev Lett, 1995, 74: 3608-3611. doi: 10.1103/PhysRevLett.74.3608 [145] Shigemori K, Nakai M, Azechi H, et al. Feed-out of rear surface perturbation due to rarefactionwave in laser-irradiated targets[J]. Phys Rev Lett, 2000, 84: 5331-5334. doi: 10.1103/PhysRevLett.84.5331 [146] Goldstein W, Rosner R. Workshop on the Science of Fusion Ignition on NIF[R]. LLNL-TR-570412, 2012. [147] 2015 review of the inertial confinement fuion and high hnergy hensity science portfolio[Z]. 2016. [148] Miller G H, Moses E I, and WuestC R. The National Ignition Facility: enabling fusion ignition for the 21st century[J]. Nucl Fusion, 2004, 44: S228. doi: 10.1088/0029-5515/44/12/S14 [149] 宋鹏, 翟传磊, 李双贵, 等. 激光间接驱动惯性约束聚变二维总体程序——LARED集成程序[J]. 强激光与粒子束, 2015, 27:032007. (Song Peng, Zhai Chuanlei, Li Shuanggui, et al. LARED-Integration code for numerical simulation of the whole process of the indirect-drive laser inertial confinement fusion[J]. High Power Laser and Particle Beams, 2015, 27: 032007 doi: 10.11884/HPLPB201527.032007 [150] Li Y S, Gu J F, Wu C S, et al. Effects of the P2 M-band flux asymmetry of laser-driven gold hohlraums on the implosion of ICF ignition capsule[J]. Phys Plasmas, 2016, 23: 072705. doi: 10.1063/1.4958811 [151] Li Y S, Zhai C L, Ren G L, et al. P2 asymmetry of Au's M-band flux and its smoothing effects due to high-Z ablator dopants[J]. Matter Radiat Extremes, 2017, 2: 69. doi: 10.1016/j.mre.2016.12.001 [152] Haan S W, Lindl J D, Callahan D A, et al. Point design targets, specifications, and requirements for the 2010 ignition campaign on the National Ignition Facility[J]. Phys Plasmas, 2011, 18: 051001. doi: 10.1063/1.3592169 [153] Yi S A, Simakov A N, Wilson D C, et al. Hydrodynamic instabilities in beryllium targets for the National Ignition Facility[J]. Phys Plasmas, 2014, 21: 092701. doi: 10.1063/1.4894112 [154] 李波, 张占文, 何智兵, 等. 激光惯性约束聚变靶靶丸制备与表征[J]. 强激光与粒子束, 2015, 27:032024. (Li Bo, Zhang Zhanwen, He Zhibing, et al. Preparation and characterization of inertial confinement fusion capsules[J]. High Power Laser and Particle Beams, 2015, 27: 032024 doi: 10.11884/HPLPB201527.032024 [155] Zhou Y. Rayleigh-Taylor and Richtmyer-Meshkov instability induced flow, turbulence, and mixing. I[J]. Physics Reports, 2017, 720: 1-136. [156] Ott E. Nonlinear evolution of the Rayleigh-Taylor instability of a thin layer[J]. Phys Rev Lett, 1972, 29: 1429. doi: 10.1103/PhysRevLett.29.1429 [157] Manheimer W, Colombant D, Ott E. Three-dimensional, nonlinear evolution of the Rayleigh-Taylor instability of a thin layer[J]. Phys Fluids, 1984, 27: 2164-2175. doi: 10.1063/1.864842 [158] Colombant D, Manheimer W, Ott E. Three-dimensional, nonlinear evolution of the Rayleigh-Taylor instability of a thin layer[J]. Phys Rev Lett, 1984, 53: 446-449. doi: 10.1103/PhysRevLett.53.446 [159] 赵凯歌. 收缩几何非线性流体力学不稳定性薄壳理论[D]. 北京: 中国工程物理研究院, 2019.Zhao Kaige. Thin Shell theory for the nonlinear hydrodynamic instability in convergent geometry[D]. Beijing: China Academy of Engineering Physics, 2019. [160] Zhao K G, Wang L F, Xue C, et al. Thin layer model for nonlinear evolution of the Rayleigh-Taylor instability[J]. Phys Plasmas, 2018, 25: 032708. doi: 10.1063/1.5009257 [161] 赵凯歌, 薛创, 王立锋, 等. 经典瑞利-泰勒不稳定性界面变形演化的改进型薄层模型[J]. 物理学报, 2018, 67:094701. (Zhao Kaige, Xue Chuang, Wang Lifeng, et al. Improved thin layer model of classical Rayleigh-Taylor instability for the deformation of interface[J]. Acta Physica Sinica, 2018, 67: 094701 doi: 10.7498/aps.67.20172613 [162] Zhao K G, Xue C, Wang L F, et al. Thin shell model for the nonlinear fluid instability of cylindrical shells[J]. Phys Plasmas, 2018, 25: 092703. doi: 10.1063/1.5044443 [163] Zhao K G, Xue C, Wang L F, et al. Two-dimensionalthin shell model for the nonlinear Rayleigh-Taylor instability in spherical geometry[J]. Phys Plasmas, 2019, 26: 022710. doi: 10.1063/1.5079316 [164] Wang L F, Guo H Y, Wu J F, et al. Weakly nonlinear Rayleigh-Taylor instability of a finite-thickness fluid layer[J]. Phys Plasmas, 2014, 21: 122710. doi: 10.1063/1.4904363 [165] Wang L F, Ye W H, Li Y J. Interface width effect on the classical Rayleigh-Taylor instability in the weakly nonlinear regime[J]. Phys Plasmas, 2010, 17: 052305. doi: 10.1063/1.3396369 [166] Mikaelian K O. Explicit expressions for the evolution of single-mode Rayleigh-Taylor and Richtmyer-Meshkov instabilities at arbitrary Atwood numbers[J]. Phys Rev E, 2003, 67: 026319. doi: 10.1103/PhysRevE.67.026319 [167] Mikaelian K O. Rayleigh-Taylor and Richtmyer-Meshkov instabilities and mixing in stratified cylindrical shells[J]. Phys Fluids, 2005, 17: 094105. doi: 10.1063/1.2046712 [168] Mikaelian K O. Rayleigh-Taylor and Richtmyer-Meshkov instabilities and mixing in stratified spherical shells[J]. Phys Rev A, 1990, 42: 3400-3420. doi: 10.1103/PhysRevA.42.3400 [169] Hurricane O A, Callahan D A, Casey D T, et al. The high-foot implosion campaign on the National Ignition Facility[J]. Phys Plasmas, 2014, 21: 056314. doi: 10.1063/1.4874330 [170] Wang L F, Wu J F, Fan Z F, et al. Coupling between interface and velocity perturbations in the weakly nonlinear Rayleigh-Taylor instability[J]. Phys Plasmas, 2012, 19: 112706. doi: 10.1063/1.4766165 [171] Wang L F, Wu J F, Ye W H, et al. Weakly nonlinear incompressible Rayleigh-Taylor instability growth at cylindrically convergent interfaces[J]. Phys Plasmas, 2013, 20: 042708. doi: 10.1063/1.4803067 [172] Zhang J, Wang L F, Ye W H, et al. Weakly nonlinear incompressible Rayleigh-Taylor instability in spherical geometry[J]. Phys Plasmas, 2017, 24: 062703. doi: 10.1063/1.4984782 [173] Layzer D. On the instability of superposed fluids in a gravitational field[J]. Astrophys J, 1955, 122(1): 1. [174] Zhang J, Wang L F, Ye W H, et al. Weakly nonlinear incompressible Rayleigh-Taylor instability in spherical and planar geometries[J]. Phys Plasmas, 2018, 25: 022701. doi: 10.1063/1.5017749 [175] Zhang J, Wang L F, Ye W H, et al. Multimode Rayleigh-Taylor instability in the weakly nonlinear regime in spherical geometry[J]. Phys Plasmas, 2018, 25: 082723. [176] Hecht J, Alon U, Shvarts D. Potential flow models of Rayleigh-Taylor and Richtmyer-Meshkov bubble fronts[J]. Phys Fluids, 1994, 6: 4019. doi: 10.1063/1.868391 [177] Sakagami H, Nishihara K. Three-dimensional Rayleigh-Taylor instability of spherical systems[J]. Phys Rev Lett, 1994, 65(4): 432. [178] Zhang J, Wang L F, Wu J F, et al. The three-dimensional weakly nonlinear Rayleigh-Taylor instability in spherical geometry[J]. Phys Plasmas, 2020, 27: 022707. doi: 10.1063/1.5128644 [179] Fryxell B, Olson K, Ricker P, et al. Flash: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes[J]. Astrophys J Suppl Ser, 2000, 131: 273-334. doi: 10.1086/317361 [180] Jacobs J W, Catton I. Three-dimensional Rayleigh-Taylor instability Part 1. Weakly nonlinear theory[J]. J Fluid Mech, 1988, 187: 329-352. doi: 10.1017/S002211208800045X [181] Haan S W. Weakly nonlinear hydrodynamic instabilities in inertial fusion[J]. Phys Fluids B, 1991, 3: 2349-2355. doi: 10.1063/1.859603 [182] Liu W H, Wang L F, Ye W H, et al. Nonlinear saturation amplitudes in classical Rayleigh-Taylor instability atarbitrary Atwood numbers[J]. Phys Plasmas, 2012, 19: 042705. doi: 10.1063/1.3702063 [183] Liu W H, Wang L F, Ye W H, et al. Temporal evolution of bubble tip velocity in classical Rayleigh-Taylor instability at arbitrary Atwood numbers[J]. Phys Plasmas, 2013, 20: 062101. doi: 10.1063/1.4801505 [184] Simakov A N, Wilson D C, Yi S A, et al. Optimized beryllium target design for indirectly driven inertial confinement fusion experiments on the National Ignition Facility[J]. Phys Plasma, 2014, 21: 022701. doi: 10.1063/1.4864331 [185] Weir S T, Chandler E A, Goodwin B T. Rayleigh-Taylor instability experiments examining feedthrough growth in an incompressible, convergent geometry[J]. Phys Rev Lett, 1998, 80(17): 3763-3766. doi: 10.1103/PhysRevLett.80.3763 [186] Shigemori K, Azechi H, Nakai M, et al. Perturbation transfer from the front to rear surface of laser-irradiated targets[J]. Phys Rev E, 2002, 65: 045401. [187] Milovich J L, Amendt P, Marinak M, et al. Multimode short-wavelength perturbation growth studies for the National Ignition Facility double-shell ignition target designs[J]. Phys Plasmas, 2004, 11(4): 1552-1568. doi: 10.1063/1.1646161 [188] Li Zhiyuan, Wang Lifeng, Wu Junfeng, et al. Phase effects of long-wavelength Rayleigh-Taylor instability on the thin shell[J]. Chinese Physics Letters, 2020, 37: 025201. doi: 10.1088/0256-307X/37/2/025201 [189] Li Zhiyuan, Wang Lifeng, Wu Junfeng, et al. Numerical study on the laser ablative Rayleigh-Taylor instability[J]. Acta Machanica Sinica, 2020,36: 789-796. [190] Li Zhiyuan, Wang Lifeng, Wu Junfeng, et al. Interface coupling effects of the weakly nonlinear Rayleigh-Taylor instability with double interfaces[J]. Chinese Physics B, 2020, 29: 034704. doi: 10.1088/1674-1056/ab6965 [191] Mikaelian K O. Time evolution of density perturbations in accelerating stratified fluids[J]. Physical Review A, 1983, 28(3): 1637-1646. doi: 10.1103/PhysRevA.28.1637 [192] Clark D S, Marinak M M, Weber C R, et al. Radiation hydrodynamics modeling of the highest compression inertial confinement fusion ignition experiment from the National Ignition Campaign[J]. Phys Plasmas, 2015, 22: 022703. doi: 10.1063/1.4906897 [193] Clark D S, Hinkel D E, Eder D C, et al. Detailed implosion modeling of deuterium-tritium layered experiments on the National Ignition Facility[J]. Phys Plasmas, 2013, 20: 056318. doi: 10.1063/1.4802194 [194] Wang L F, Wu J F, Guo H Y, et al. Weakly nonlinear Bell-Plesset effects for a uniformly converging cylinder[J]. Phys Plasmas, 2015, 22: 082702. doi: 10.1063/1.4928088 [195] Ofer D, Alon U, Shvarts D, et al. Modal model for the nonlinear multimode Rayleigh-Taylor instability[J]. Phys Plasmas, 1996, 3: 3073-3090. doi: 10.1063/1.871655 [196] Vandenboomgaerde M, Gauther S, Mugler C. Nonlinear regime of a multimode Richtmyer-Meshkov instability: A simplified perturbation theory[J]. Phys Fluids, 2002, 14: 1111-1122. doi: 10.1063/1.1447914 [197] Hsing W W, Barnes C W, Beck J B, et al. Rayleigh–Taylor instability evolution in ablatively driven cylindrical implosions[J]. Phys Plasmas, 1997, 4: 1832. doi: 10.1063/1.872326 [198] Ikegawa T, Nishihara K. Ablation effects on weakly nonlinear Rayleigh-Taylor instability with a finite bandwidth[J]. Phys Rev Lett, 2002, 89: 115001. doi: 10.1103/PhysRevLett.89.115001 [199] Sanz J, Ramirez J, Ramis R, et al. Nonlinear theory of the ablative Rayleigh-Taylor instability[J]. Phys Rev Lett, 2002, 89: 195002. doi: 10.1103/PhysRevLett.89.195002 [200] Garnier J, Raviart P A, Cherfils-Clerouin C, et al. Weakly nonlinear theory for the ablative Rayleigh-Taylor instability[J]. Phys Rev Lett, 2003, 90: 185003. doi: 10.1103/PhysRevLett.90.185003 [201] Jiang Y, Shu C W, Zhang M. An alternative formulation of finite difference weighted ENO schemes with Lax-Wendroff time discretization for conservation laws[J]. SIAM J Sci Comput, 2013, 35(2): A1137-A1160. doi: 10.1137/120889885 [202] Liu X D, Osher S, Chan T. Weighted essentially non-oscillatory schemes[J]. J Comput Phys, 1994, 115(1): 200-212. doi: 10.1006/jcph.1994.1187 [203] Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. J Comput Phys, 1996, 126(1): 202-228. doi: 10.1006/jcph.1996.0130 [204] Castro M, Costa B, Don W S. High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws[J]. J Comput Phys, 2011, 230(5): 1766-1792. doi: 10.1016/j.jcp.2010.11.028 [205] Borges R, Carmona M, Costa B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J]. J Comput Phys, 2008, 227(6): 3191-3211. doi: 10.1016/j.jcp.2007.11.038 [206] Wang B S, Li P, Gao Z, et al. An improved fifth order alternative WENO-Z finite difference scheme for hyperbolic conservation laws[J]. J Comput Phys, 2018, 374: 469-477. doi: 10.1016/j.jcp.2018.07.052 [207] Gao Z, Fang L L, Wang B S, et al. Seventh and ninth orders alternative WENO finite difference schemes for hyperbolic conservation laws[J]. Comput Fluids, 2020, 202. [208] Xing Y, Shu C W. High order well-balanced WENO scheme for the gas dynamics equations under gravitational fields[J]. J Sci Comput, 2013, 54: 645-662. doi: 10.1007/s10915-012-9585-8 [209] Zhang X X, Shu C W. Positivity-preserving high order finite difference WENO schemes for compressible Euler equations[J]. J Comput Phys, 2012, 231(5): 2245-2258. doi: 10.1016/j.jcp.2011.11.020 [210] Luo J, Xu K, Liu N. A well-balanced symplecticity-preserving gas-kinetic scheme for hydrodynamic equations under gravitational field[J]. SIAM J Sci Comput, 2011, 33: 2356-2381. doi: 10.1137/100803699 [211] Zylstra A B, MacLaren S, Yi S A, et al. Implosion performance of subscale beryllium capsules on the NIF[J]. Phys Plasmas, 2019, 26: 052702. doi: 10.1063/1.5086674 [212] Bose A, Betti R, Shvarts D, et al. The physics of long- and intermediate-wavelength asymmetries of the hot spot: compression hydrodynamics and energetics[J]. Phys Plasmas, 2017, 24: 102704. doi: 10.1063/1.4995250 [213] Goncharov V N, Gotchev O V, Vianello E, et al. Early stage of implosion in inertial confinement fusion: Shock timing and perturbation evolution[J]. Phys Plasms, 2006, 13: 012702. doi: 10.1063/1.2162803 [214] Wu J F, Miao W Y, Wang L F, et al. Indirect-drive ablative Rayleigh-Taylor growth experiments on the Shenguang-II laser facility[J]. Phys Plasmas, 2014, 21: 042707. doi: 10.1063/1.4871721 [215] Ye W H, Wang L F, He X T. Spike deceleration and bubble acceleration in the ablative Rayleigh-Taylor instability[J]. Phys Plasmas, 2010, 17: 122704. doi: 10.1063/1.3497006 -





 下载:
下载: