Application of coulomb collision cross-section in particle-in-cell simulation of plasma
-
摘要: 在等离子体粒子模拟中，TA模型和NanBu模型被广泛用于处理库仑碰撞，这两种模型要求每个时间步长内全部粒子参与计算。为了降低参与碰撞的粒子数，提高库仑碰撞的计算效率，提出了一种基于截面的库仑碰撞模拟方法，并给出了库仑碰撞概率的计算公式。采用该方法对不同温度不同密度电子气的弛豫过程进行模拟，分别对比了电子速度分布函数、电子温度以及电子x、y方向上的温度与电子温度之比的模拟值与理论值，验证了该方法的准确性。在相同的小时间步长上，该方法相比TA模型计算效率提升可达40%以上。对于较大的时间步长，该方法仍能得到与理论解近似的模拟结果，相比Nanbu模型，在相同的精度下可取更大的时间步长，计算效率也有所提升。研究表明，该方法同样适用于电子-离子碰撞。因此在提高库仑碰撞计算效率上，该方法具有碰撞粒子数少以及适用于大时间步长的优势。Abstract: In particle-in-cell simulation of plasma, TA and Nanbu models have been widely used for Coulomb collision. Both models require all particles to collide. In this paper, a cross-section-based method is introduced to give a probability of Coulomb collision for each particle pair and accelerate the computation. To test this method, the relaxations of an electron gas due to e-e collisions were simulated. Comparing the simulated with the theoretical values of velocity distribution function, electron temperature, the ratio of electron temperature in x, y direction to electron temperature, the accuracy of the cross-section-based method was verified. The calculation efficiency of this method can be improved by more than 40% than the TA model at the same small time step. Furthermore, at a large time step, the simulations show agreement with the theoretical solutions, the efficiency is also improved than the Nanbu model. The simulation about the equilibration of electron and ion temperature showes that this method is also suitable for e-i collisions. Therefore in the acceleration of simulating Coulomb collision, this method has two advantages as follows: first, there is a small number of particles to collide within a step, and second, it is suitable for large time steps.
-
图 2 （电子-电子碰撞）不同库仑碰撞截面下电子x, y方向的温度与电子温度之比的模拟值和理论值随时间的变化
Figure 2. (e-e collision) The time evolution of the ratio of electron temperature in x, y direction to electron temperature: the simulation and theoretical values with different Coulomb collision cross sections
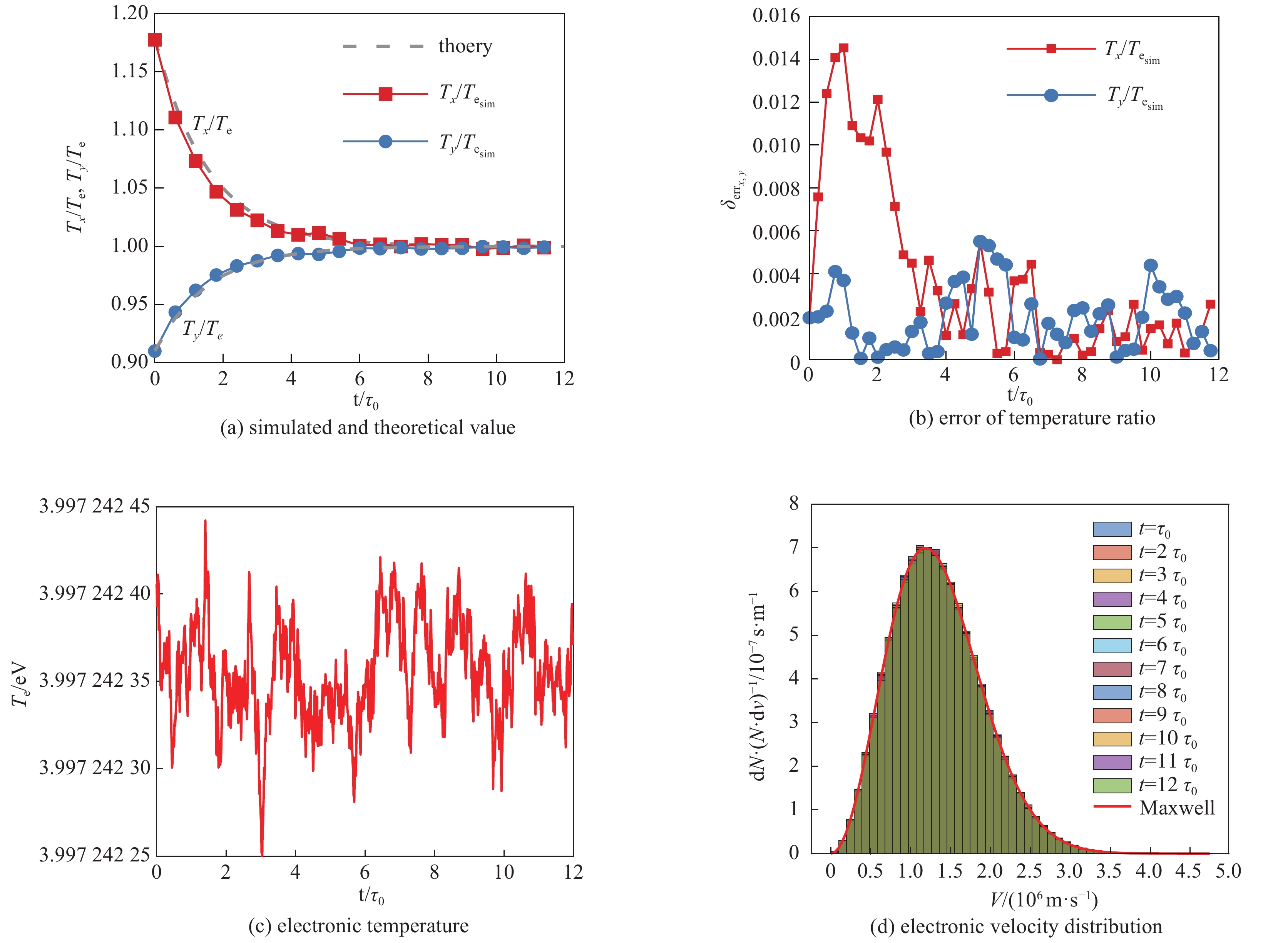
图 3 （电子-电子碰撞）截面法模拟过程中，（a）电子x, y方向的温度与电子温度之比的模拟值和理论值，（b）温度之比的模拟值与理论值之差，（c）电子温度以及（d）电子速度分布函数随时间的变化
Figure 3. (e-e collision) With cross-section method, the time evolution of (a) the simulated and the theoretical values of the ratio of electron temperature in x, y direction to electron temperature, (b) the difference between the simulated and the theoretical values of the temperature ratio, (c) the temperature of electron, and (d) the velocity distribution function of electron
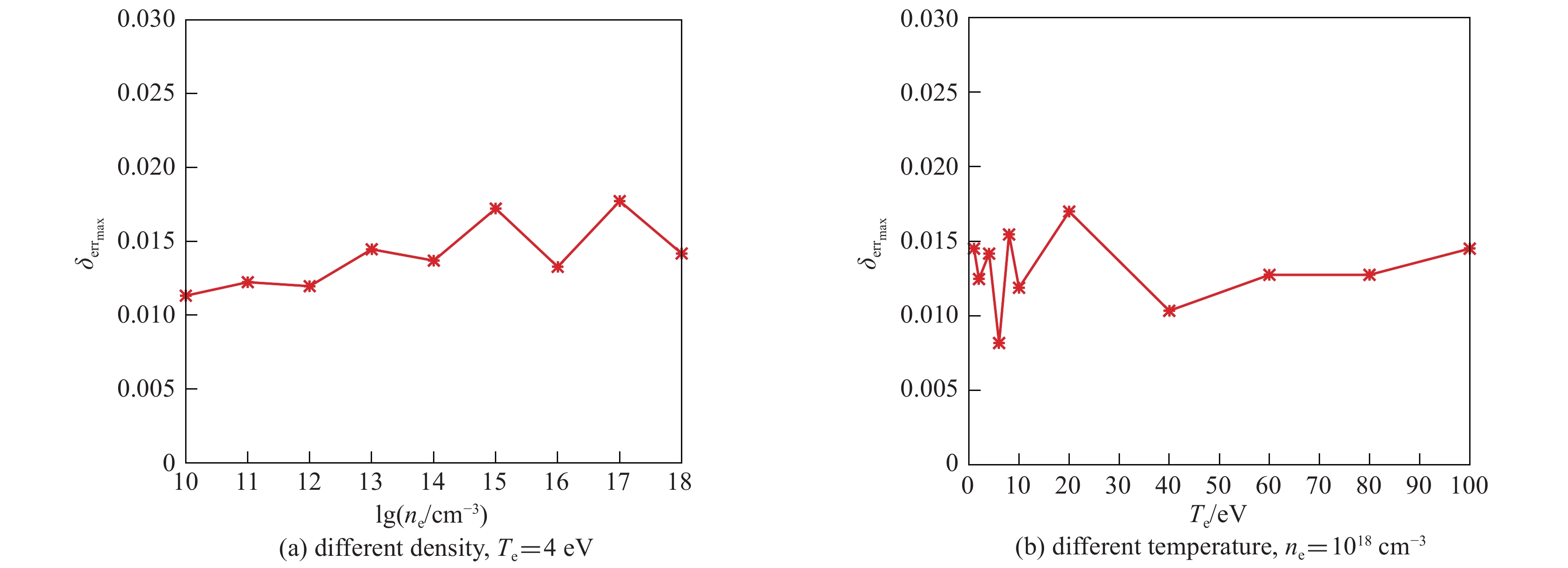
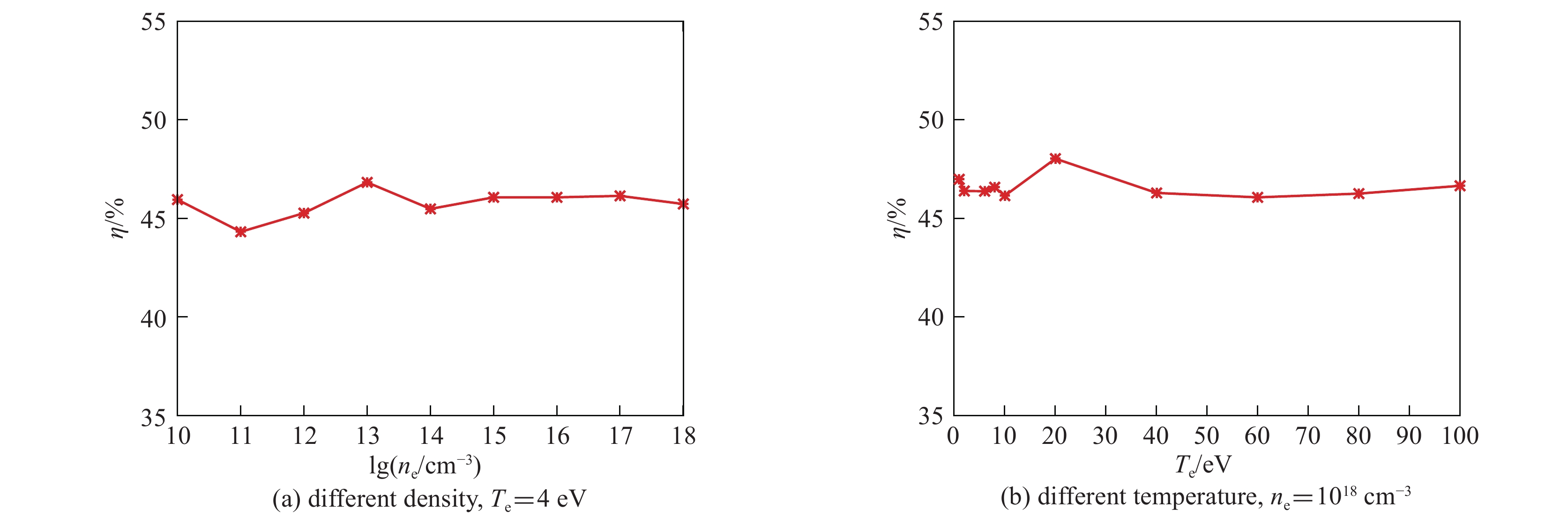
图 4 （电子-电子碰撞）不同温度密度条件下，截面法模拟过程中电子x,y方向的温度与电子温度之比的模拟值和理论值之差的统计结果
Figure 4. (e-e collision) With cross-section method, the maximum results of the difference between the simulated and theoretical values of the ratio of the electron temperature in the x, y direction to the electron temperature with different temperature and density of electron
图 5 （电子-电子碰撞）不同温度密度条件下截面法相比TA模型的计算效率提升
Figure 5. (e-e collision) The improvement of calculation efficiency of the cross-section method, compared with the TA model with different temperature and density of electron
图 6 （电子-电子碰撞）截面法和TA模型在不同时间步长下，电子x方向的温度与电子温度之比的模拟结果和理论值随时间的变化
Figure 6. (e-e collision) Under different time steps, the time evolution of the ratio of electron temperature in x direction to electron temperature: the simulation and theoretical values with cross-section method and TA model
图 7 （电子-电子碰撞）不同时间步长，相同温度密度条件下截面法和Nanbu模型相比TA模型的计算效率提升
Figure 7. (e-e collision) The improvement of calculation efficiency of the cross-section method and Nanbu model, compared with the TA model under different time step with the same temperature and density of electron
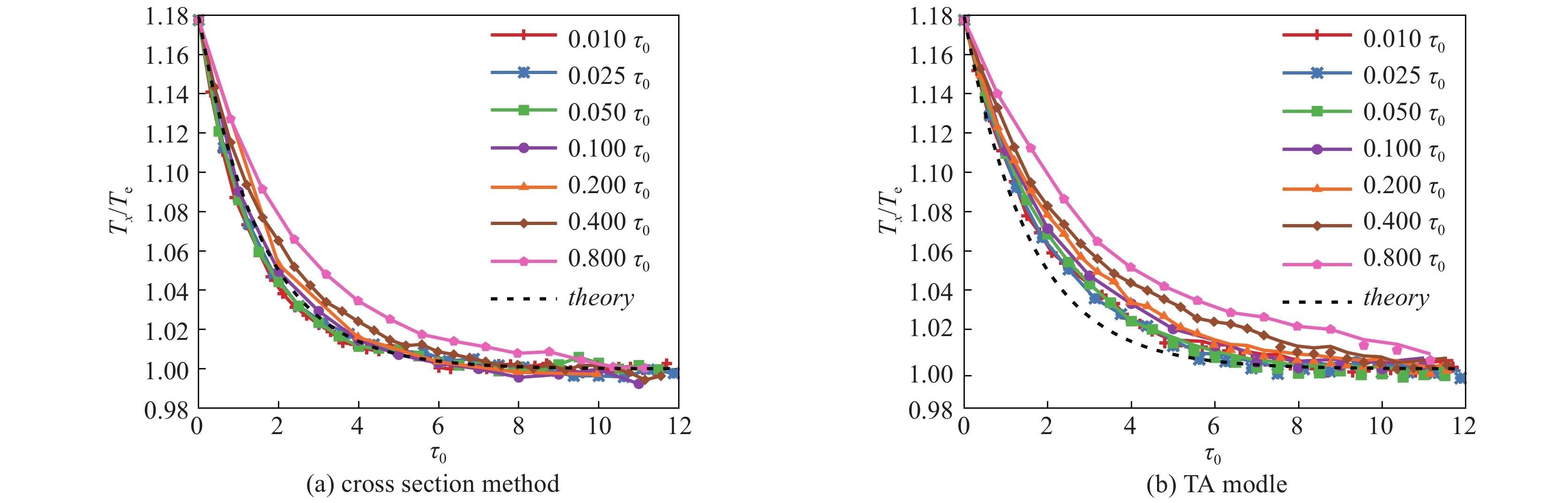
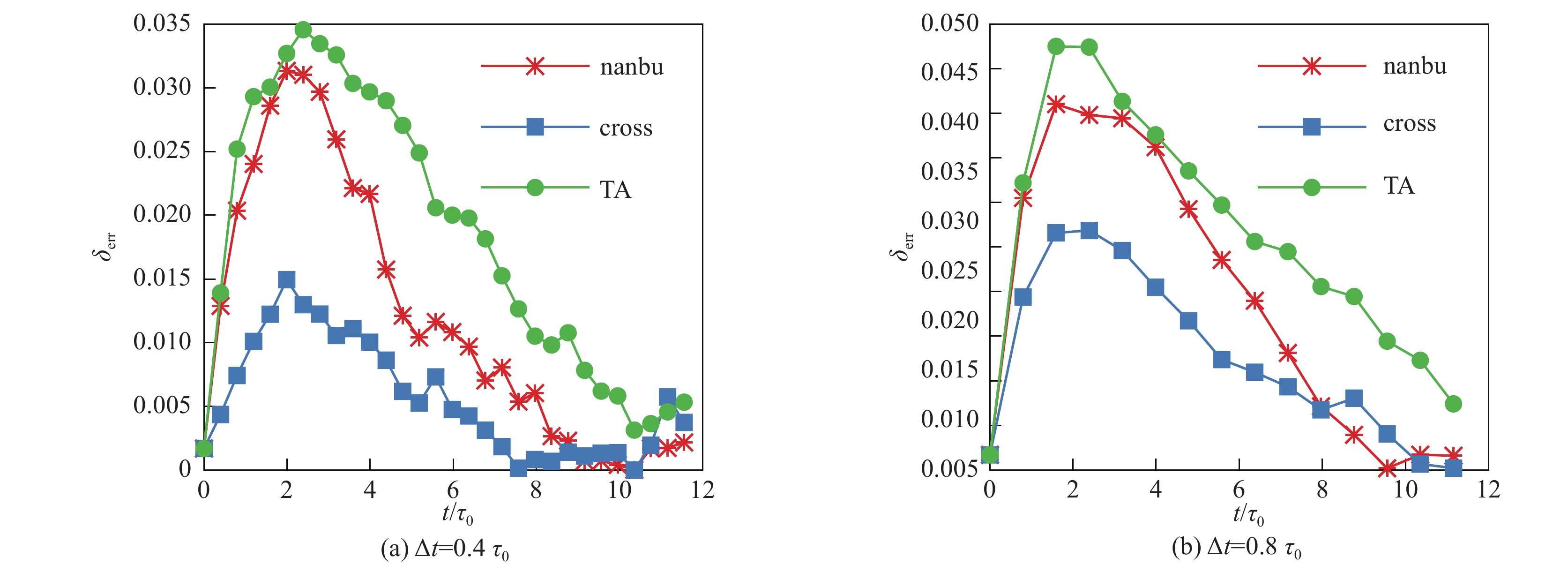
图 8 （电子-电子碰撞）截面法，TA模型Nanbu模型在不同时间步长下，电子x方向的温度与电子温度之比的模拟值和理论值之差随时间的变化
Figure 8. (e-e collision) Under different time steps, the time evolution of the maximum results of the difference between the simulated and theoretical values of the ratio of the electron temperature in the x direction to the electron temperature with cross-section method, TA model and Nanbu model
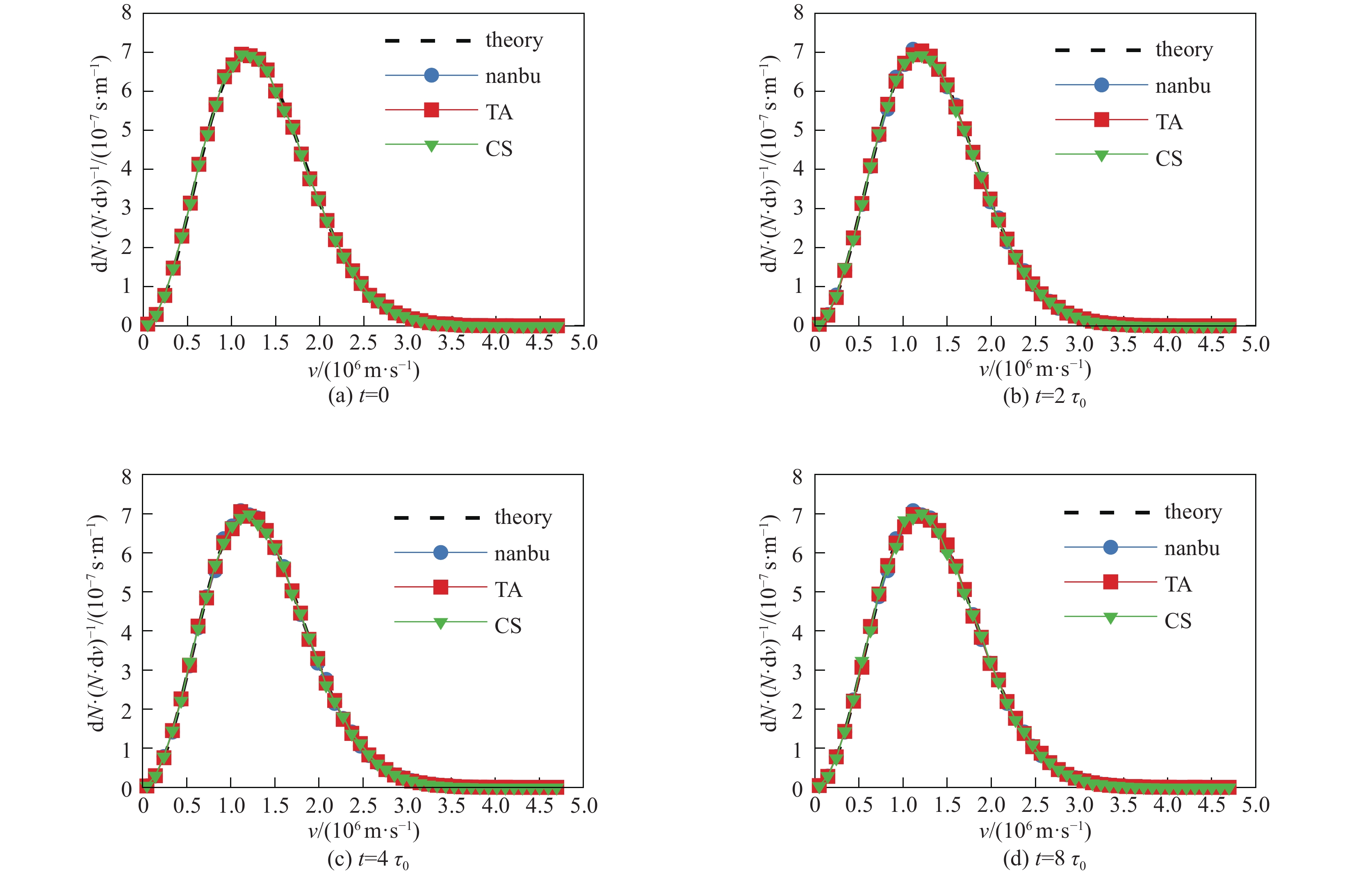
图 9 （电子-电子碰撞）截面法，TA模型Nanbu模型在相同时间步长下，模拟过程中不同时刻电子速度分布函数的模拟值和理论值的比较
Figure 9. (e-e collision) Under the same time step, the simulation and the theoretical values of the velocity distribution function at different time in the simulation process are compared by cross-section method, TA model and Nanbu model
图 10 （电子-离子碰撞）截面法模拟过程中，（a）电子和离子温度与平衡温度之比的模拟值和理论值，（b）温度之比的模拟值与理论值之差（c）电子离子温度之和以及（d）电子速度分布函数随时间的变化
Figure 10. (e-i collision) With cross-section method, the time evolution of (a) the simulated and the theoretical values of the ratio of electron temperature and ion temperature to equilibration temperature, (b) the difference between the simulated and the theoretical values of the temperature ratio, (c) the sum of temperature of electron and ion (d) the velocity distribution function of electron
-
[1] Hagelaar G J M, Donko Z, Dyatko N. Modification of the Coulomb logarithm due to electron-neutral collisions[J]. Physical Review Letters, 2019, 123: 025004. doi: 10.1103/PhysRevLett.123.025004 [2] Birdsall C K. Particle-in-cell charged-particle simulations, plus Monte Carlo collisions with neutral atoms[J]. IEEE Transactions on Plasma Science, 1991, 19(2): 65-85. doi: 10.1109/27.106800 [3] Takizuka T, Abe H. A binary collision model for plasma simulation with a particle code[J]. Journal of Computational Physics, 1977, 25(3): 205-219. doi: 10.1016/0021-9991(77)90099-7 [4] Veske M, Kyritsakis A, Djurabekova F. Dynamic coupling between particle-in-cell and atomistic simulations[J]. Physical Review E, 2020, 101: 053307. doi: 10.1103/PhysRevE.101.053307 [5] 杨超, 刘大刚, 王小敏, 等. 基于负氢离子源的全三维PIC/MCC 模拟算法研究[J]. 物理学报, 2012, 61:045204. (Yang Chao, Liu Dagang, Wang Xiaomin, et al. A three-dimensional particle-in-cell/Monte Carlo computer simulation based on negative hydrogen ion source[J]. Acta Physica Sinica, 2012, 61: 045204 doi: 10.7498/aps.61.045204 [6] Nanbu K. Theory of cumulative small-angle collisions in plasmas[J]. Physical Review E—Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1997, 55(4): 4642-4652. [7] 王辉辉, 杨超, 刘大刚, 等. Ta及Nanbu库仑碰撞模型数值对比研究[J]. 物理学报, 2013, 62:015206. (Wang Huihui, Yang Chao, Liu Dagang, et al. Numerical comparison between Ta and Nanbu models of Coulomb collisions[J]. Acta Physica Sinica, 2013, 62: 015206 doi: 10.7498/aps.62.015206 [8] Dominguez-Vázquez A, Taccogna F, Ahedo E. Particle modeling of radial electron dynamics in a controlled discharge of a Hall thruster[J]. Plasma Sources Science and Technology, 2018, 27: 064006. doi: 10.1088/1361-6595/aac968 [9] Wang C, Lin T, Caflisch R, et al. Particle simulation of Coulomb collisions: Comparing the methods of Takizuka & Abe and Nanbu[J]. Journal of Computational Physics, 2008, 227(9): 4308-4329. doi: 10.1016/j.jcp.2007.12.027 [10] Caflisch R, Wang R, Dimarco G, Dimarco, et al. A hybrid method for accelerated simulation of Coulomb collisions in a plasma[J]. Multiscale Model Simul, 2008, 7(2): 865-887. doi: 10.1137/070704939 [11] Ricketson L F, Rosin M S, Caflisch R E, et al. An entropy based thermalization scheme for hybrid simulations of Coulomb collisions[J]. Journal of Computational Physics, 2014, 273: 77-99. doi: 10.1016/j.jcp.2014.04.059 [12] Lemons D S, Winske D, Daughton W, et al. Small-angle Coulomb collision model for particle-in-cell simulations[J]. Journal of Computational Physics, 2009, 228(5): 1391-1403. doi: 10.1016/j.jcp.2008.10.025 [13] Vahedi V, Surendra M. A Monte Carlo collision model for the particle-in-cell method: applications to argon and oxygen discharges[J]. Computer Physics Communications, 1995, 87(1/2): 179-198. [14] Sjobak K, Helga T. 2D ArcPIC code description: description of methods and user/developer manual (Second Edition)[R]. CLIC-Note-1032, 2014. [15] 姜巍. 射频容性耦合等离子体的两维隐格式PIC/MC模拟[D]. 大连理工大学, 2010: 33-34.Jiang Wei. Two-dimensional implicit PIC/MC simulations for radio-frequency capacitively coupled plasma[D]. Dalian: Dalian University of Technology, 2010: 33-34 [16] 徐家鸾, 金尚宪. 等离子体物理学[M]. 北京: 原子能出版社, 1981: 34-37.Xu Jialuan, Jin Shangxian. Plasma physics[M]. Beijing: Atomic Energy Press, 1981: 34-37 [17] Diver D A. Plasma formulary for physics, astronomy, and technology[M]. Germany: Wiley-VCH Verlag GmbH & Co. KGaA, 2013: 91-92 -
下载:
点击查看大图
计量
- 文章访问数: 1441
- HTML全文浏览量: 266
- PDF下载量: 105
- 被引次数: 0
