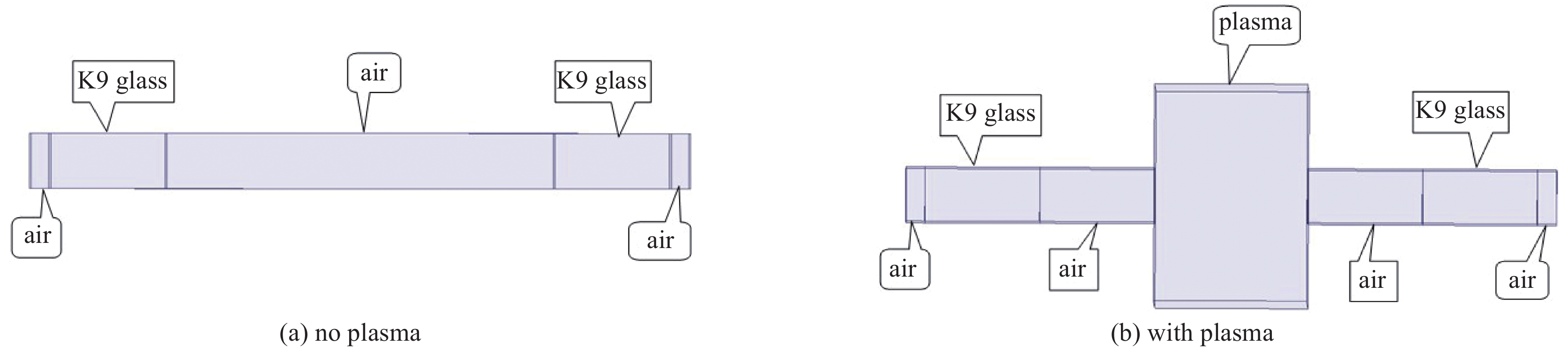
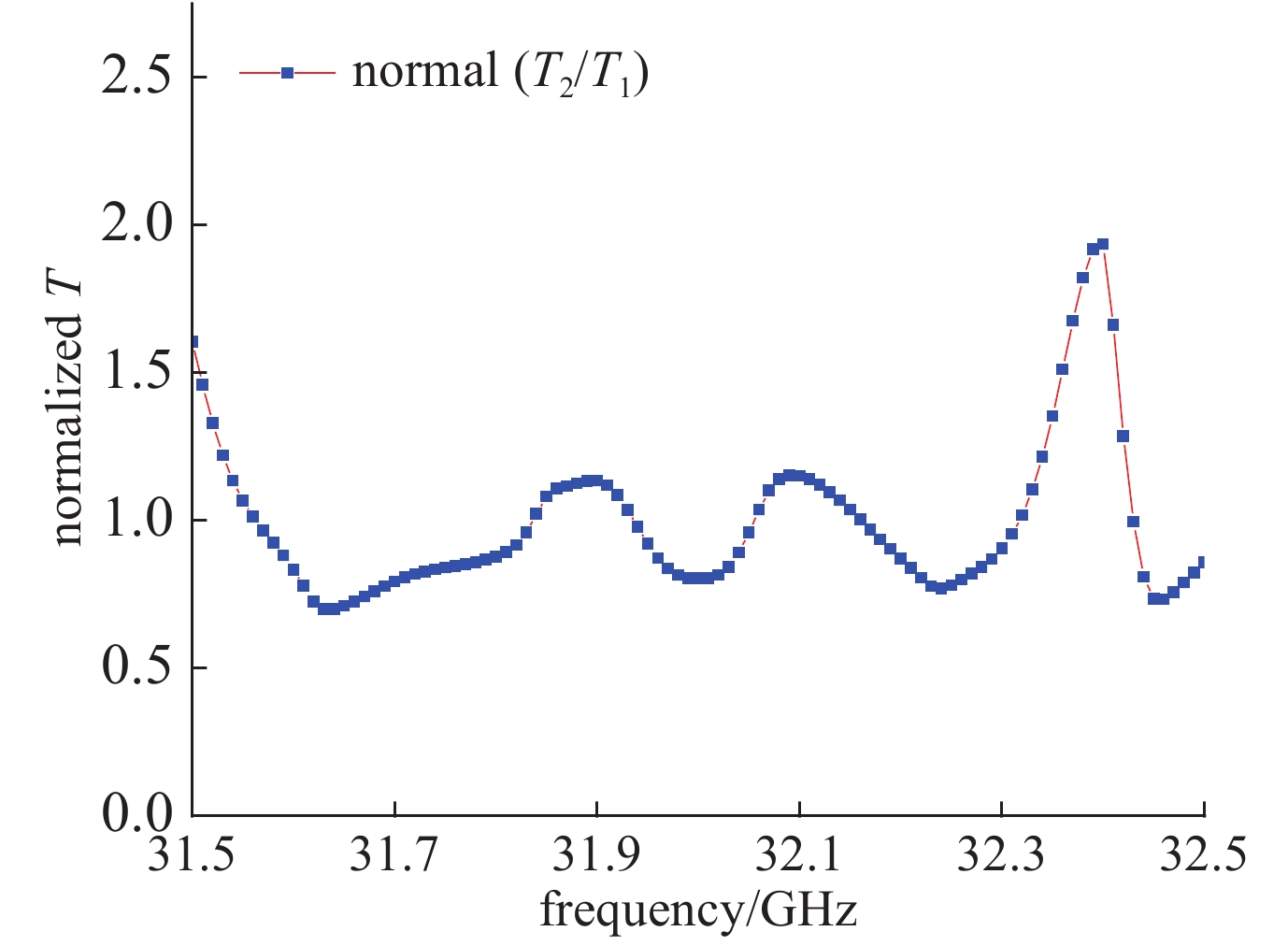
| [1] |
王家胜, 杨显强, 经姚翔, 等. 钝头型航天器再入通信黑障及对策研究[J]. 航天器工程, 2014, 23(1):6-16. (Wang Jiasheng, Yang Xianqiang, Jing Yaoxiang, et al. On the communication blackout during reentry of blunt-nosed spacecraft and its eliminating approaches[J]. Spacecraft Engineering, 2014, 23(1): 6-16 doi: 10.3969/j.issn.1673-8748.2014.01.002
|
| [2] |
王志斌, 孔繁荣, 鄂鹏, 等. 再入航天器表面亚波长等离子体薄层对微波信号影响效应研究[J]. 中国空间科学技术, 2017, 37(1):111-116. (Wang Zhibin, Kong Fanrong, E Peng, et al. Dumping effect of microwave signal in plasma slabs with sub-wavelength characteristics around spacecraft[J]. Chinese Space Science and Technology, 2017, 37(1): 111-116
|
| [3] |
闫二艳, 杨浩, 郑强林, 等. 瞬变等离子体微波诊断初步研究[J]. 强激光与粒子束, 2019, 31:103207. (Yan Eryan, Yang Hao, Zheng Qianglin, et al. Principium study of the microwave diagnostics for transient temperature plasma[J]. High Power Laser and Particle Beams, 2019, 31: 103207 doi: 10.11884/HPLPB201931.190175
|
| [4] |
杨浩, 闫二艳, 郑强林, 等. 临近空间高功率微波辐照放电试验技术[J]. 强激光与粒子束, 2019, 31:103216. (Yang Hao, Yan Eryan, Zheng Qianglin, et al. Examination research of high power microwave irradiation discharge in near space[J]. High Power Laser and Particle Beams, 2019, 31: 103216 doi: 10.11884/HPLPB201931.190151
|
| [5] |
Vidmar R J. On the use of atmospheric pressure plasmas as electromagnetic reflectors and absorbers[J]. IEEE Trans Plasma Science, 1990, 18(4): 733-741. doi: 10.1109/27.57528
|
| [6] |
Gregoire D J, Santoru J, Schumacher R W. Electromagnetic-wave propagation in unmagnetized plasmas[R]. AD-A250710, 1992.
|
| [7] |
Laroussi M. Scattering of electromagnetic waves by a layer of air plasma surrounding a conducting cylinder[J]. International Journal of Infrared & Millimeter Waves, 1996, 17(12): 2215-2232.
|
| [8] |
Laroussi M, Roth J R. Numerical calculation of the reflection, absorption, and transmission of microwaves by a nonuniform plasma slab[J]. IEEE Trans Plasma Science, 2002, 21(4): 366-372.
|
| [9] |
Kalluri D K, Lee J H, Ehsan M M. FDTD simulation of electromagnetic pulse interaction with a switched plasma slab[J]. International Journal of Infrared & Millimeter Waves, 2003, 24(3): 349-365.
|
| [10] |
Kim H C, Verboncoeur J P. Reflection, absorption and transmission of TE electromagnetic waves propagation in a nonuniform plasma slab[J]. Computer Physics Communications, 2007, 177(1): 118-121.
|
| [11] |
Samimi A, Simpson J J. An efficient 3-D FDTD model of electromagnetic wave propagation in magnetized plasma[J]. IEEE Trans Antennas & Propagation, 2014, 63(1): 269-279.
|
| [12] |
Soliman E A, Helaly A, Megahed A A. Propagation of electromagnetic waves in planar bounded plasma region[J]. Prog Electromagn Res, 2007, 67: 25-37. doi: 10.2528/PIER06071102
|
| [13] |
Gürel C S, Öncü E. Frequency selective characteristics of a plasma layer with sinusoidally-varying electron density profile[J]. Journal of Infrared Millimeter & Terahertz Waves, 2009, 30(6): 589-597.
|
| [14] |
Zhang Shu, Hu Xiwei, Jiang Zhonghe, et al. Propagation of an electromagnetic wave in an atmospheric pressure plasma: Numerical solutions[J]. Physics of Plasmas, 2006, 13(1): 2618-2630.
|
| [15] |
Yuan Chengxun, Zhou Zhongxiang, Zhang Jingwen, et al. Propagation of terahertz waves in an atmospheric pressure microplasma with Epstein electron density profile[J]. Journal of Applied Physics, 2011, 109(6): 1189.
|
| [16] |
Hu Binjie, Wei Guang, Lai Shengli. SMM analysis of reflection, absorption, and transmission from nonuniform magnetized plasma slab[J]. IEEE Trans Plasma Science, 1999, 27(4): 1131-1136. doi: 10.1109/27.782293
|
| [17] |
Kong X K, Yang H W, Liu S B, et al. Research on the reflection, absorption and transmission of electromagnetic waves for inhomogeneous magnetized plasma[C]//International Conference on Microwave and Millimeter Wave Technology. 2008.
|
| [18] |
赵朋程, 郭立新, 李慧敏. 110 GHz高功率微波在大气击穿等离子体中的传输、反射和吸收[J]. 电波科学学报, 2016, 31(3):512-515. (Zhao Pengcheng, Guo Lixin, Li Huiming. Transmission, reflection and absorption of 110 GHz high-power microwave in air breakdown plasma[J]. Chinese Journal of Radio Science, 2016, 31(3): 512-515
|
| [19] |
周前红, 董志伟, 陈京元. 110 GHz 微波电离大气产生等离子体过程的理论研究[J]. 物理学报, 2011, 60(12):349-360. (Zhou Qianhong, Dong Zhiwei, Chen Jingyuan. Modeling of plasma pattern formation in 110 GHz microwave air breakdown[J]. Acta Physica Sinica, 2011, 60(12): 349-360
|
| [20] |
Destler W W, Degrange J E, Fleischmann H H, et al. Experimental studies of high-power microwave reflection, transmission, and absorption from a plasma-covered plane conducting boundary[J]. Journal of Applied Physics, 1991, 69(9): 6313-6318. doi: 10.1063/1.348829
|
| [21] |
Koretzky E, Kuo S P. Characterization of an atmospheric pressure plasma generated by a plasma torch array[J]. Physics of Plasmas, 1998, 5(10): 3774-3780. doi: 10.1063/1.872741
|
| [22] |
马平, 曾学军, 石安华, 等. 电磁波在等离子体高温气体中传输特性实验研究[J]. 实验流体力学, 2010, 24(5):51-56. (Ma Ping, Zeng Xuejun, Shi Anhua, et al. Experimental investigation on electromagnetic wave transmission characteristic in the plasma high temperature gas[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(5): 51-56 doi: 10.3969/j.issn.1672-9897.2010.05.011
|
| [23] |
郑灵, 赵青, 罗先刚, 等. 等离子体中电磁波传输特性理论和实验研究[J]. 物理学报, 2012, 61(15):343-349. (Zheng Ling, Zhao Qing, Luo Xiangang, et al. Theoretical and experimental studies of electromagnetic wave transmission in plasma[J]. Acta Physica Sinica, 2012, 61(15): 343-349
|
| [24] |
刘新芽. 电磁波在多层介质内的透射[J]. 光学学报, 1995, 15(1):122-125. (Liu Xinya. The transmisson of electromagnetic waves in multilayer media[J]. Acta Opticia Sinica, 1995, 15(1): 122-125 doi: 10.3321/j.issn:0253-2239.1995.01.025
|
| [25] |
周琦, 刘新芽. 多层介质中电磁波的反射与透射[J]. 南昌大学学报(理科版), 2003, 23(1):37-44. (Zhou Qi, Liu Xinya. The reflection and transmission of electromagnetic wave in multilayer media[J]. Journal of Nanchang University(Natural Science), 2003, 23(1): 37-44
|
| [26] |
江遴汉, 张祖荣. 电磁波在均匀薄膜上的反射和透射[J]. 物理与工程, 2014(s2):9-12. (Jiang Linhan, Zhang Zurong. Reflection and transmission of electromagnetic wave on uniform film[J]. Physics and Engineering, 2014(s2): 9-12
|
| [27] |
Epstein P S. Reflection of waves in an inhomogeneous absorbing medium[J]. Proc NaR Acad Sci Wash, 1930, 16(10): 627-637. doi: 10.1073/pnas.16.10.627
|




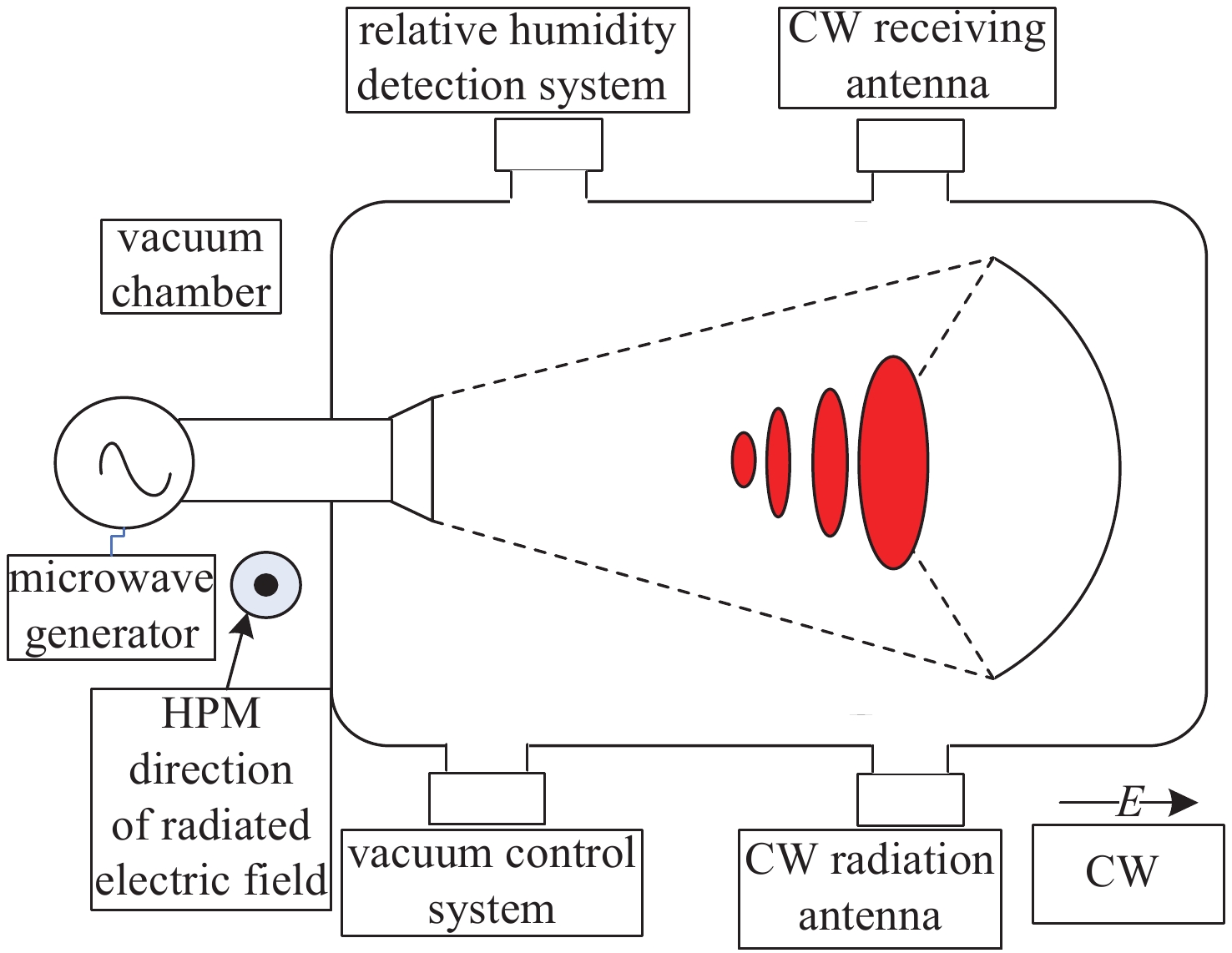
 下载:
下载: