-
氚作为核电站常见的放射性产物之一，半衰期长，易进入环境且易被生物体吸收，放射性危害大。压水堆中铀核三元裂变产生的氚经由燃料元件包壳进入一回路，是冷却剂中氚的重要来源，约占冷却剂中氚总量的20%[1]。《核动力厂环境辐射防护规定》[2]基于堆型、装机容量等对氚的年排放限值做了相关规定。氚在燃料包壳材料的扩散迁移行为对氚的排放有重要影响。
国内外对氚扩散行为的研究日益深入，许多学者对锆及其合金以及氧化锆中氚扩散进行了实验研究，如Kearns[3]、Kunz[4]、Khatamain[5]、Smith[6]等，通过实验给出了一定温度范围内氢同位素在锆合金或氧化锆内的扩散系数。由于实验方法及工况不同，各学者的研究结果略有差异。总体上看，多数学者的研究结果在同一数量级，但由于不同研究结果的扩散激活能项有较大区别，温度较高时扩散系数会出现很严重的分散现象。许多机构对氚在材料中的扩散模拟也开展了较多研究，基于Sievert定律的扩散通量计算方法，或基于Fick定律的扩散方程差分求解方法，开发了氢及其同位素在结构材料中扩散的一维模拟程序。典型程序有橡树岭国家实验室（ORNL）开发的TRITGO[7]，爱达荷国家实验室（INL）开发的TPAC[8]和TMAP[9]，日本原子能机构（JAEA）开发的THYTAN[10]以及由韩国高级科学技术研究所开发的TBEC[11]。TRITGO、THYTAN、TPAC为大范围氚迁移程序，可覆盖全堆计算。TBEC与TMAP则专门针对氚在结构材料中的扩散，采用基于Fick定律的扩散方程差分求解方法，与Sievert定律方法相比，更加关注氚在结构材料中的扩散行为。此外，INL在燃料性能一体化模拟3-D程序Bison[12]中也集成了氢在燃料包壳中的扩散模型，将包壳简化为单层材料考虑。目前氚扩散相关模拟研究主要关注氚的总体渗透量，边界模型选取基于溶解平衡的分压-浓度公式[13]，实际对于未达到溶解平衡的扩散过程，比如氚在压水堆燃料包壳的扩散，可能高估了氚在包壳中的滞留量以及整体包壳的渗透量。目前氚扩散模拟研究对结构中的温度分布的影响关注较低，多数采用平均温度或有效平均温度对整体结构温度进行表征[14]。反应堆燃料包壳存在明显的温度梯度并且表面存在氧化层，对氚扩散行为有较大影响。目前国内反应堆燃料元件氚释放量均参考运行经验进行计算[15]，因此针对锆合金包壳中的氚扩散问题开发专门方法进行模拟研究具有较高的研究意义与应用价值。本文基于氢同位素在材料中的扩散模型建立了一维模拟程序，对氢同位素扩散典型实验进行了模拟验证，并对不同氚浓度、氧化层厚度、温度分布下氚在锆合金包壳材料中的扩散进行了分析。
-
氢同位素在结构材料中的扩散可以分为3个过程：（1）气体从源项腔室通过溶解进入结构表面；（2）在结构中的扩散；（3）在另一侧表面的解吸进入其他腔室。扩散过程受温度分布、浓度分布、扩散率、多层结构等因素影响。
-
氢原子在结构中的扩散过程高度依赖于温度变化，因此，采用经典导热微分方程模拟燃料包壳的结构热响应，即
$$ \rho {C_{\rm{p}}}\frac{{\partial T}}{{\partial t}} = \nabla \left( {\kappa \nabla T} \right) + {S_{\rm{h}}} $$ (1) 式中：
$\;\rho $ 为材料密度，kg/m3；${C_{\rm{p}}}$ 为定压比热容，J/（kg·K）；$\kappa $ 为热导率，W/（m·K）；${S_{\rm{h}}}$ 为本地热源，W。当两层材料存在热接触时，两层材料的接触面通常会形成一个绝缘层，起到抑制热传递的作用。采用间隙换热系数表征多层模型的接触面热阻，如公式（2）。当两层接触面传热良好时，可认为接触面传热系数很大，即
$T_f^A = T_f^B$ 。$$ - \kappa {\left. {\frac{{\partial T}}{{\partial x}}} \right|_{{f^A}}} = - \kappa {\left. {\frac{{\partial T}}{{\partial x}}} \right|_{{f^B}}} = {h_{{\rm{gap}}}}\left( {T_f^A - T_f^B} \right) $$ (2) 式中：
$T_{\rm{f}}^A$ 为该时刻的材料A表面节点温度，K；$T_{\rm{f}}^B$ 为该时刻的材料B表面节点温度，K；${h_{{\rm{gap}}}}$ 为表面换热系数，W/（m2·K）。 -
当氢同位素在结构材料中存在化学势梯度，如浓度梯度、温度梯度等，就会导致扩散。由于浓度梯度导致的扩散符合Fick定律，如公式（3），即在稳态扩散的条件下，单位时间内通过垂直于扩散方向的单位面积的扩散物质量与该截面处的浓度梯度成正比。氢同位素的扩散速度也受到温度分布的影响，温度升高则扩散速度加快，如公式（4）。
$$ { {{J}}_{{\rm{Fick}}}} = - D(\nabla C) $$ (3) 式中：
$C$ 为固溶氚浓度，Atom/m3；${{{ J}}_{{\rm{Fick}}}}$ 为Fick定律扩散通量，Atom/（m2·s）；$D$ 为扩散系数，m−1。$$ D = {D_{\rm{0}}}\exp ( - {Q_D}/RT) $$ (4) 式中：
$D$ 为扩散系数，m2/s${D_{\rm{0}}}$ 为扩散常数；${Q_D}$ 为扩散激活能，J/mol；$R$ 为理想气体常数，8.314 J/（mol·K）。对于氢的三种同位素氕、氘、氚，理论上认为其扩散率之比与其原子量的平方根成反比，即
$$ {D_H}:{D_D}:{D_T} = 1:\frac{1}{{\sqrt 2 }}:\frac{1}{{\sqrt 3 }} $$ (5) Sawatzky[16]研究发现，材料中温度梯度的存在不仅影响扩散系数，还可能会直接驱动扩散，这种现象称为热致扩散效应。热致扩散通量表达式为
$$ {{{ J}}_{{\rm{Soret}}}} = - D\frac{{{Q^*}C}}{{R{T^2}}}\nabla T $$ (6) 式中：
${{{ J}}_{{\rm{Soret}}}}$ 为热致扩散通量，atom/（m2·s）；${Q^*}$ 为扩散热，kJ/mol。综上，存在温度梯度的材料中氢同位素的扩散是热梯度扩散和浓度梯度扩散的耦合结果，即
$$ \frac{{\partial C}}{{\partial t}} = \nabla \cdot ({{{ J}}_{{\rm{Fick}}}} + {{{J}}_{{\rm{Soret}}}}) - \lambda C $$ (7) 式中：
$t$ 为时间，s；$\lambda $ 为衰变常数，s−1。 -
本文采用一维差分网格模型，其中腔室节点设置为单节点/无网格，腔室不考虑空间尺度。腔室-结构的连接通过建立边界零厚度表面节点实现。网格划分如图1。
图 1 网格示意图
Figure 1. Diagram of the grid
-
2010年，日本京都大学I.Takagi[17]等人及日本核燃料发展公司完成了250～400 ℃下，氘在锆合金氧化层中的扩散实验。所使用的锆合金材料为GNF-Ziron（高铁锆合金）和VB（高铁铬锆合金）。实验将试件放置在400 ℃的D2O蒸汽中10～15 d，得到氧化层厚度为1.4～1.7 µm的预腐蚀试件。氧化层内部具有两种结构：扩散速度相对快的外部非保护氧化层和扩散速度较慢的内部阻挡层。扩散过程中，样品表面的氘浓度保持不变，氘粒子通过表面，经过非保护氧化层、内部阻挡层向内部进行扩散。该研究明确给出了300 ℃工况下，氘在GNF-Ziron以及VB锆合金的两种氧化层的扩散率，并运用HYDIF程序进行了模拟计算并与实验结果比对。
本文对GNF-Ziron以及VB锆合金进行建模。整体温度保持300 ℃不变，建立了由两层氧化层和一层金属层组成的计算系统，氧化层表面氘浓度恒定。具体实验参数如表1。
表 1 氘扩散实验参数表
Table 1. Parameters of the deuterium diffusion experiment
case thickness
(outer oxide layer)/μmthickness
(inner oxide layer)/μmsurface area/cm2 diffusion coefficient
(in outer oxide layer)/(cm2/s)diffusion coefficient
(in inner oxide layer)/(cm2/s)GNF-Ziron 0.5 1 4 2.2×10−13 1.6×10−14 VB 0.68 0.82 4 4.2×10−14 7.4×10−15 将模拟结果与实验值以及HYDIF计算值进行比对，如图2所示。结果表明：本模拟结果与实验值和HYDIF模拟结果符合较好，两层氧化层不同的扩散率导致的浓度梯度趋势变化也符合较好，总体误差保持在5%以内。当存在多层结构时，各层结构内的浓度梯度会因扩散系数不同而产生差异。对于GNF-Ziron算例，由于外氧化层的扩散系数较高，该层氘浓度梯度明显较小。对于VB算例，由于两层结构的扩散率比值与GNF-Ziron算例相比要低，因此两层结构的浓度梯度变化较小，但外层浓度梯度仍比内层浓度梯度低。
图 2 模拟与实验结果对比
Figure 2. Comparison of calculation and experiment results
-
ORNL针对Surry核电站2号机组取出的燃料元件包壳进行了氚释放实验[18]，平均燃耗为36 GWd/MTU，包壳材料为锆-4合金。燃料棒样品去除燃料仅保留包壳并切成长度5～6 mm段以测试氚含量。每段包壳沿周向平均切成3份试件，将每个包壳中的一个样品加热到1100～1200 ℃，使锆完全氧化并释放包壳样品中的所有氚，以测定包壳中的初始氚浓度。Surry-2试件中氚的初始浓度为每克247.2 μSv，将Surry-2试件在500 ℃下加热24 h，实验结果发现，氚的总释放份额约为0.2%。
根据实验温度，氧化锆氚扩散率公式采用Smith扩散率[6]，锆-4合金氚扩散率采用Kearns扩散率[3]。对经过长时间水化学及应力腐蚀的锆包壳，其整个氧化层并非全部具有保护层的作用，外部氧化层的疏松结构已致该部分氧化层失去阻氚效果。实际具有保护作用的致密氧化层在反应堆运行过程中厚度处于动态平衡，最终其厚度大约稳定在2 μm左右[19]。模型基本参数如表2。
表 2 Surry-2燃料包壳氚释放实验参数
Table 2. Parameters of the tritium diffusion experiment of Surry-2 fuel caldding
parameter external diameter of
cladding/mminner diameter of
cladding/mmheight/mm surface area/m2 temperature/K burnup/
(GWd/MTU)thickness of dense
oxide layer/μmvalue 5.359 4.742 5.5 8.72664×10−5 773 36 2 Surry-2氚释放实验氚释放份额随时间变化的模拟结果如图3所示。随着扩散时间进行，试件的氚释放份额持续增大。计算结果与实验结果符合很好，24 h氚的释放份额为0.191%，与实验结果误差为4.5%。
图 3 Surry-2实验氚释放份额随时间变化的模拟结果
Figure 3. Simulation results of tritium release fraction in Surry-2 experiment
-
基于Surry核电站2号反应堆燃料元件的包壳模型，计算了包壳内氚分压不同时，氚在包壳中的扩散过程。由于冷却剂空间较包壳体积大很多，氧化层外表面氚浓度可以近似为零。氧化锆氚扩散率公式采用Smith扩散公式，锆-4合金氚扩散率采用Kearns扩散公式。设定包壳内氚分压为10、100、1000 Pa对计算结果进行分析，如图4所示。图4（a）表明，随着包壳间隙内氚分压的提高，氚在包壳内的浓度提高，包壳内表面氚进入通量提高，随着扩散进行，包壳内氚扩散趋于平衡。包壳间隙内氚分压越大，氚扩散进入包壳中的量越大。图4（b）表明，不同氚分压下包壳外表面出氚通量值随氚分压的提高而提高，整体变化趋势是一致的。氚分压提高会导致包壳内整体氚浓度提高，当氧化层内的氚浓度随时间升高，则氧化层内部与氧化层表面的浓度梯度提高，会引起氧化层表面氚逸出通量随时间提高。
图 4 不同氚分压情况下模拟结果对比
Figure 4. Comparison of calculation results under different tritium partial pressure
-
不同的温度条件下，结构材料的氚扩散率可能存在较大差别，特别是在温度超过773 K时，燃料包壳结构内的氚扩散率上升速度很快。由于氧化层的氚扩散率受温度变化影响很大，温度梯度条件下与恒定温度条件下氚的扩散行为也存在较大差距。基于Surry核电站2号反应堆包壳模型，模拟了包壳温度分布对氚扩散过程的影响。设定包壳固定温度为623 K、773 K以及外表面653 K、内表面593 K线性温度分布进行计算，如图5所示。
图 5 不同温度分布情况下模拟结果对比
Figure 5. Comparison of calculation results under different temperature
对于两个采用恒定温度的计算结果，温度较高初始时刻进入包壳内的扩散通量小，在较短的时间内，773 K条件下的包壳内表面氚进入通量达到稳定，并且平衡值与623 K条件下的平衡值相比高近30倍。温度较高时最初进入包壳内的扩散通量低是因为包壳表面的氚溶解量随温度的升高而降低，但不会直接导致近平衡状态下进入包壳的氚通量降低，平衡状态下进入包壳的氚通量还与整个包壳的氚渗透速率有关，773 K条件下包壳外表面氧化层的扩散系数比623 K下提高2个数量级，包壳的氚渗透速率提高，从而导致近平衡状态下进入包壳的氚通量较高。与氚分压对氧化层表面出氚通量线性影响不同，温度变化对氧化层表面出氚量影响结果更大，从数据中看是温度对出氚通量的影响为指数级。773 K条件与623 K条件计算结果相比，氧化层表面出氚通量相差107～108次方，这是因为773 K与623 K条件下，氧化层扩散系数相差3～4个数量级，高温强化了氧化层中氚向外部扩散的速率。623 K条件与线性梯度温度分布条件计算结果相比，氧化层表面出氚通量更大，这与两个固定结构温度计算结果差异的原因基本类似，由于线性梯度温度分布条件下氧化层的温度较平均温度623 K要低，因此氚在氧化层中的扩散率较低，表面的相对低温限制了氧化层中氚向外部扩散的速率。
若考虑热致扩散对氚扩散行为的影响，根据Kammenzind[20]等人研究结果，锆合金的热扩散量约为25.1 kJ/mol，对存在温度梯度的计算模型中引入热扩散系数进行模拟计算，将考虑与未考虑热致扩散影响的锆合金内氚浓度分布情况进行对比。从对比结果图6中可得，锆合金包壳内的热致扩散有利于氚从包壳的热侧向冷测迁移，这可能导致包壳表面的出氚通量提高。实际反应堆运行过程中热致扩散的影响需要更深入的研究，本文计算结果可作为初步参考。
图 6 锆合金中氚浓度分布
Figure 6. Simulation results of distribution of tritium concentration in zircaloy
-
本文基于氢同位素扩散基本数学物理模型通过自编程建立了氢同位素扩散一维模拟程序，并采用典型锆合金氢同位素扩散实验对程序进行了验证。对氚在锆合金包壳材料中扩散行为的影响因素进行了分析，得到如下结论：（1）包壳氧化层对氚扩散具有较强阻挡作用，相同扩散系数的氧化层厚度越高，对氚扩散的阻挡作用越强；（2）包壳-芯块间隙内氚浓度的升高会导致进出包壳氚扩散通量提高，渗透通量增大，但扩散份额不变，对氚在包壳内扩散行为的整体趋势影响较小；（3）温度变化对氚在包壳内扩散速率影响较大，温度对出氚扩散通量的影响为指数级。对于存在温度梯度的氚扩散行为，锆合金外表面氧化层的相对低温限制了氚渗透出包壳管的速率；（4）温度梯度导致的热致扩散有利于氚向包壳冷测扩散。
Numerical simulation and experimental verification on the diffusion behavior of tritium in zirconium alloy cladding materials
-
摘要: 基于氚扩散基本模型建立了氚扩散行为一维模拟程序，对模拟程序进行了典型实验验证，模拟结果与实验结果符合较好。分析了不同氚浓度、温度分布对锆合金包壳材料中氚的扩散行为的影响。分析结果表明：包壳-芯块间隙内氚浓度的升高会导致进出包壳的氚扩散通量提高，渗透通量增大；由于包壳氧化层相对较低的扩散系数，包壳氧化层的存在对氚渗透有较大的限制作用；温度对氚扩散速率的影响很显著，温度越高，扩散速度越快；锆合金外表面氧化层的相对低温限制了氚渗透出包壳管的速率，温度梯度导致的热致扩散有利于氚向包壳冷测扩散。Abstract: The research on the diffusion behavior of tritium in zirconium alloy is a crucial problem for nuclear power plant radiation safety evaluation. Based on the basic model of tritium diffusion, a one-dimensional simulation program for the behavior of tritium diffusion was established in this work. The simulation program was verified by typical experiments, and the simulation results were in good agreement with the experimental results. The effects of different concentration and temperature distribution of tritium on the diffusion behavior of tritium in zirconium alloy cladding materials were analyzed. The results show that the increase of tritium concentration in P-C gap lead to the increase of tritium diffusion flux and permeability flux in and out of cladding. Due to the relatively low diffusion coefficient of the coated oxide layer, the existence of the coated oxide layer limits the tritium permeability greatly. The effect of temperature on the diffusion rate of tritium is exponential. The higher the temperature is, the faster the diffusion rate is. The relative low temperature of the oxide layer on the outer surface of zirconium alloy limits the rate of tritium permeation out of the cladding tube. Thermally induced diffusion due to temperature gradient is beneficial to limit the permeation flux of tritium diffusing out of the zirconium cladding.
-
Key words:
- tritium /
- zirconium alloy /
- diffusion /
- numerical simulation
-
图 3 Surry-2实验氚释放份额随时间变化的模拟结果
Figure 3. Simulation results of tritium release fraction in Surry-2 experiment
图 4 不同氚分压情况下模拟结果对比
Figure 4. Comparison of calculation results under different tritium partial pressure
图 5 不同温度分布情况下模拟结果对比
Figure 5. Comparison of calculation results under different temperature
图 6 锆合金中氚浓度分布
Figure 6. Simulation results of distribution of tritium concentration in zircaloy
表 1 氘扩散实验参数表
Table 1. Parameters of the deuterium diffusion experiment
case thickness
(outer oxide layer)/μmthickness
(inner oxide layer)/μmsurface area/cm2 diffusion coefficient
(in outer oxide layer)/(cm2/s)diffusion coefficient
(in inner oxide layer)/(cm2/s)GNF-Ziron 0.5 1 4 2.2×10−13 1.6×10−14 VB 0.68 0.82 4 4.2×10−14 7.4×10−15 
下载: 导出CSV
表 2 Surry-2燃料包壳氚释放实验参数
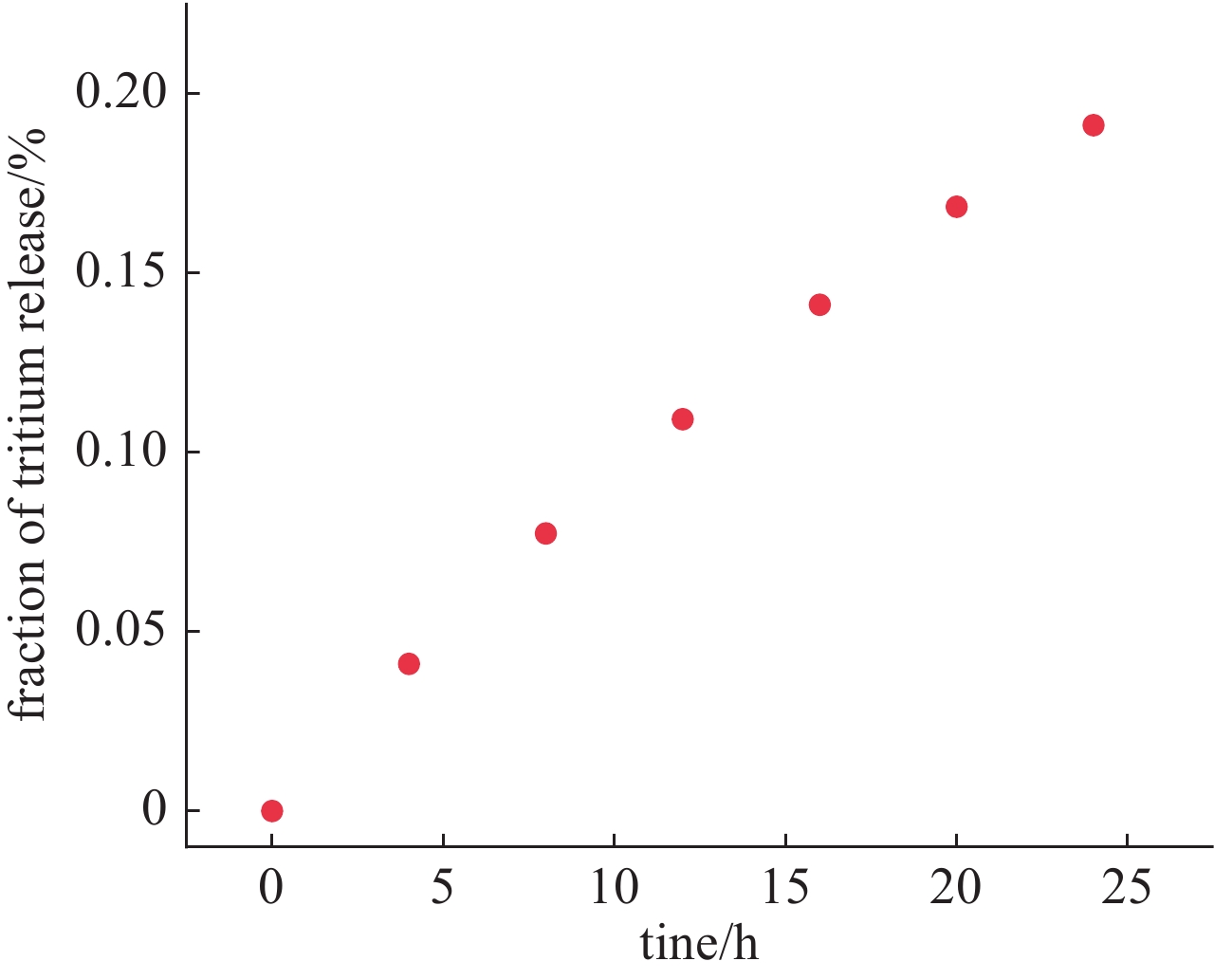
Table 2. Parameters of the tritium diffusion experiment of Surry-2 fuel caldding
parameter external diameter of
cladding/mminner diameter of
cladding/mmheight/mm surface area/m2 temperature/K burnup/
(GWd/MTU)thickness of dense
oxide layer/μmvalue 5.359 4.742 5.5 8.72664×10−5 773 36 2
下载: 导出CSV
-
[1] 陈海英, 张春明, 王韶伟. 压水堆3H源项计算分析[J]. 原子能科学技术, 2016, 50(2):459-463. (Chen Haiying, Zhang Chunming, Wang Shaowei. Calculation analysis of tritium source term in PWR[J]. Atomic Energy Science and Technology, 2016, 50(2): 459-463 [2] GB 6249-2011. 核动力厂环境辐射防护规定[S]. GB 6249-2011. Regulations for environmental radiation protection of nuclear power plant[S] [3] Kearns J J. Diffusion coefficient of hydrogen in alpha zirconium, zircaloy-2, zircaloy-4[J]. Journal of Nuclear Materials, 1972, 43: 330-338. doi: 10.1016/0022-3115(72)90065-7 [4] Kunz W, Greger G U, Munzel H. Diffusion of tritium in zircaloy-2[J]. Journal of Nuclear Materials, 1980, 88: 15-22. doi: 10.1016/0022-3115(80)90381-5 [5] Khatamian D. Diffusion of hydrogen in single crystals of monoclinic-ZrO2 and yttrium stabilized cubic zirconia[J]. Defect and Diffusion Forum, 2010, 297/301: 631-640. doi: 10.4028/www.scientific.net/DDF.297-301.631 [6] Smith T. Kinetics and mechanism of hydrogen permeation of oxide films on zirconium[J]. Journal of Nuclear Materials, 1966, 18(3): 323-336. doi: 10.1016/0022-3115(66)90173-5 [7] Hanson D L, Richards M B, Connors G P.TRIGO code description and user’s guide[R], GA-20128-911081, 2006. [8] Eung S K, Chang H O, Patterson M. Study on the tritium behaviors in the VHTR system. Part 1: Development of tritium analysis code for VHTR and verification[J]. Nuclear Engineering and Design, 2010, 240: 1758-1767. doi: 10.1016/j.nucengdes.2010.02.023 [9] Longhurst G R. TMAP7 User Manual[R]. INL/EXT-04-02352, 2004. [10] Ohashi H, Sherman S. Tritium movement and accumulation in the NGNP system interface and hydrogen production[R]. INL/EXT-07-12746, 2007. [11] Yook D, Lee K J, Lee Y, et al. Estimation of the tritium behavior in the pebble type gas cooled reactor for hydrogen production[J]. Nuclear Science and Techniques, 2006, 43: 1522-1529. doi: 10.1080/18811248.2006.9711249 [12] Aly A, Avramova M, Ivanov K, et al. Three dimensional fuel pin model validation by prediction of hydrogen distribution in cladding and comparison with experiment[R]. DOE-NEUP-13-5180, 2017. [13] Yamanaka S, Miyake M, Katsura M. Hydrogen solubility in zirconium alloys[J]. Journal of Nuclear Materials, 1995, 247(1/2): 315-321. [14] Park M Y, Kim B Y, Kim E S. Development of semi-empirical model for tritium permeation under non-uniform temperature distribution at heat exchanger tube wall[J]. Annals of Nuclear Energy, 2015, 75: 413-420. doi: 10.1016/j.anucene.2014.08.044 [15] 黎辉, 梅其良, 付亚茹. 核电厂氚的产生和排放分析[J]. 原子能科学技术, 2015, 49(4):739-743. (Li Hui, Mei Qiliang, Fu Yaru. Analysis of generation and release of tritium in nuclear power plant[J]. Atomic Energy Science and Technology, 2015, 49(4): 739-743 doi: 10.7538/yzk.2015.49.04.0739 [16] Sawatzky A. The diffusion and solubility of hydrogen in the alpha-phase of zircaloy-2[J]. Journal of Nuclear Materials, 1960, 2(1): 62-68. doi: 10.1016/0022-3115(60)90025-8 [17] Takagi I, Une K, Miyamura S, et al. Deuterium diffusion in steam-corroded oxide layer of zirconium alloys[J]. Journal of Nuclear Material, 2011, 419: 339-346. doi: 10.1016/j.jnucmat.2011.06.001 [18] Robinson S M, Chattin M R, Giaquinto J M, et al. Evaluation of tritium content and release from pressurized water reactor fuel cladding[R]. ORNL/SPR-2015/425, 2015. [19] Barberis P, Frichet A. Characterization of zircaloy-4 oxide layers by impedance spectroscopy[J]. Journal of Nuclear Materials, 1999, 273: 182-191. doi: 10.1016/S0022-3115(99)00025-2 [20] Kammenzind B F, Franklin D G, Peters H R, et al. Hydrogen pickup and redistribution in alpha-annealed zircaloy-4[C]//11th International Symp on Zr in the Nuclear Industry. 1996: 338-370. -
点击查看大图
图(6) / 表 (2)
计量
- 文章访问数: 42
- HTML全文浏览量: 11
- PDF下载量: 6
- 被引次数: 0
