Research progress of propagation of beams with special correlation structure in turbulent atmosphere
-
摘要:
近年来,光场调控逐渐成为光学领域的热点研究课题,光场相干性调控可以引发许多新颖物理效应。其中,通过相干性调控得到的特殊关联结构光束不仅展现出奇特的传输特性,而且可以有效地降低大气湍流引起的光强退化、光束漂移、光强闪烁和退偏振等负面效应。因此,特殊关联结构光束在自由空间光通信领域具有重要的应用前景。本文回顾了特殊关联结构光束的构建基础理论和大气传输研究方法及其发展历程,举例展示近些年典型特殊关联结构光束的大气传输研究成果。
Abstract:In recent years, optical fields manipulation has become a hot research topic and optical coherence manipulation can induce many novel physical effects. The laser beams with special correlation structure obtained by coherence control not only exhibit peculiar propagation characteristics, but also can effectively reduce the negative effects induced by atmospheric turbulence, such as intensity degradation, beam wander, scintillation and depolarization. Thus, these beams have applications prospects in free-space optical communications. In this paper, the basic theory of the construction of special correlation structure beams and the research methods as well as their development history are reviewed, and the propagation properties of special correlation structure beams in turbulent atmosphere in recent years are illustrated as examples.
-
Key words:
- correlation structure /
- coherence /
- atmospheric turbulence /
- propagation properties
-
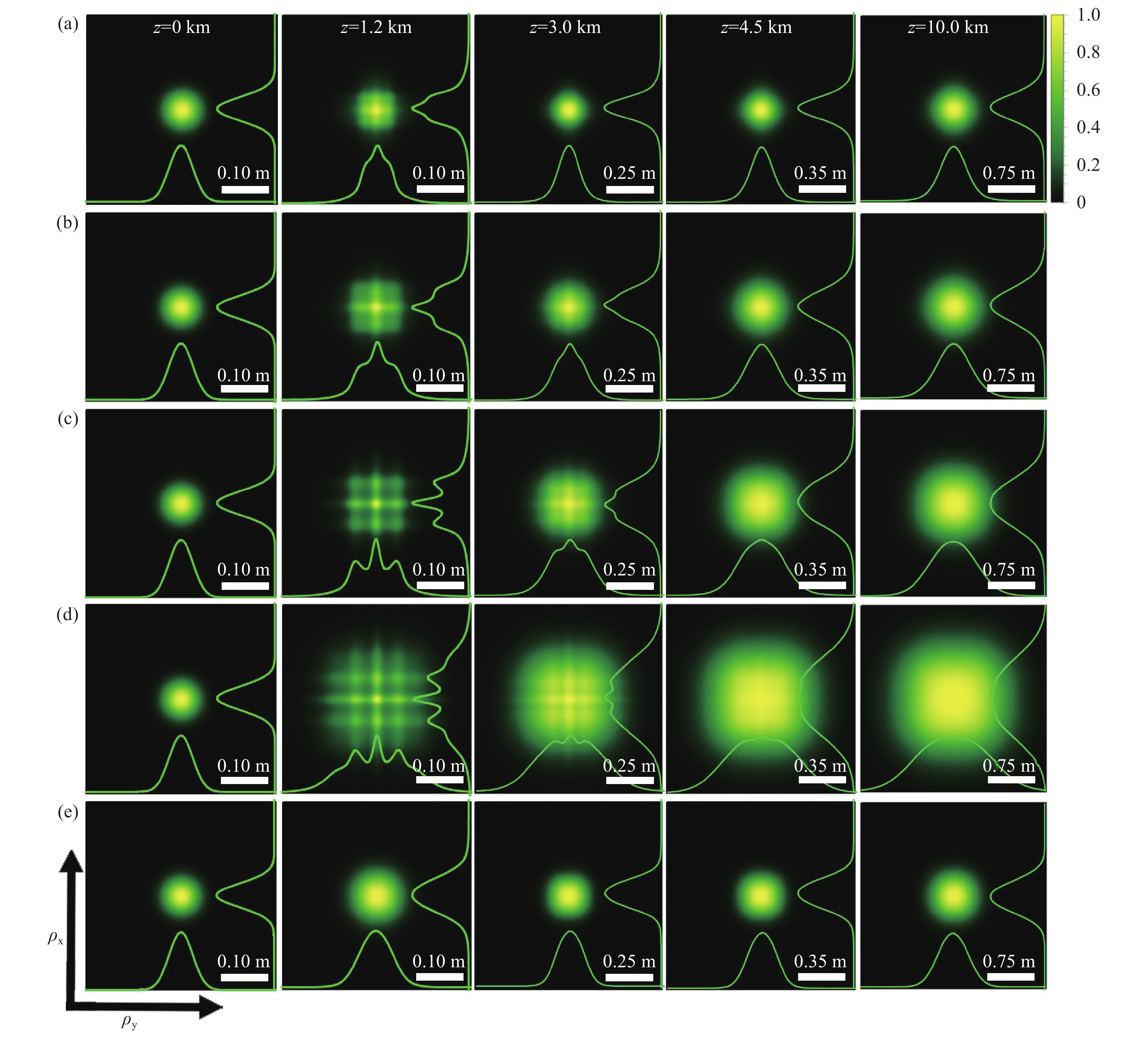
图 10 厄米非均匀关联结构阵列光束在湍流大气中光强演化图(a)m = 1,p = q = 1,rc= 3 cm,x0= y0= 3 cm;(b)m = 1,p = q = 1,rc= 3 cm,x0= y0= 5 cm;(c)m = 2,p = q = 1,rc= 3 cm,x0= y0= 5 cm;(d)m = 2,p =q = 2,rc= 3 cm,x0= y0= 5 cm;(e)m = 2,p = q = 2,rc= 5 cm,x0= y0= 5 cm[67]
Figure 10. Evolution of spectral intensity of Hermite non-uniformly correlated array beams with (a) m = 1,p = q = 1,rc= 3 cm,x0= y0= 3 cm;(b) m = 1,p = q = 1,rc= 3 cm,x0= y0= 5 cm;(c) m = 2,p = q = 1,rc= 3 cm,x0= y0= 5 cm;(d) m = 2,p =q = 2,rc= 3 cm,x0= y0= 5 cm;(e) m = 2,p = q = 2,rc= 5 cm,x0= y0= 5 cm in turbulent atmosphere[67]
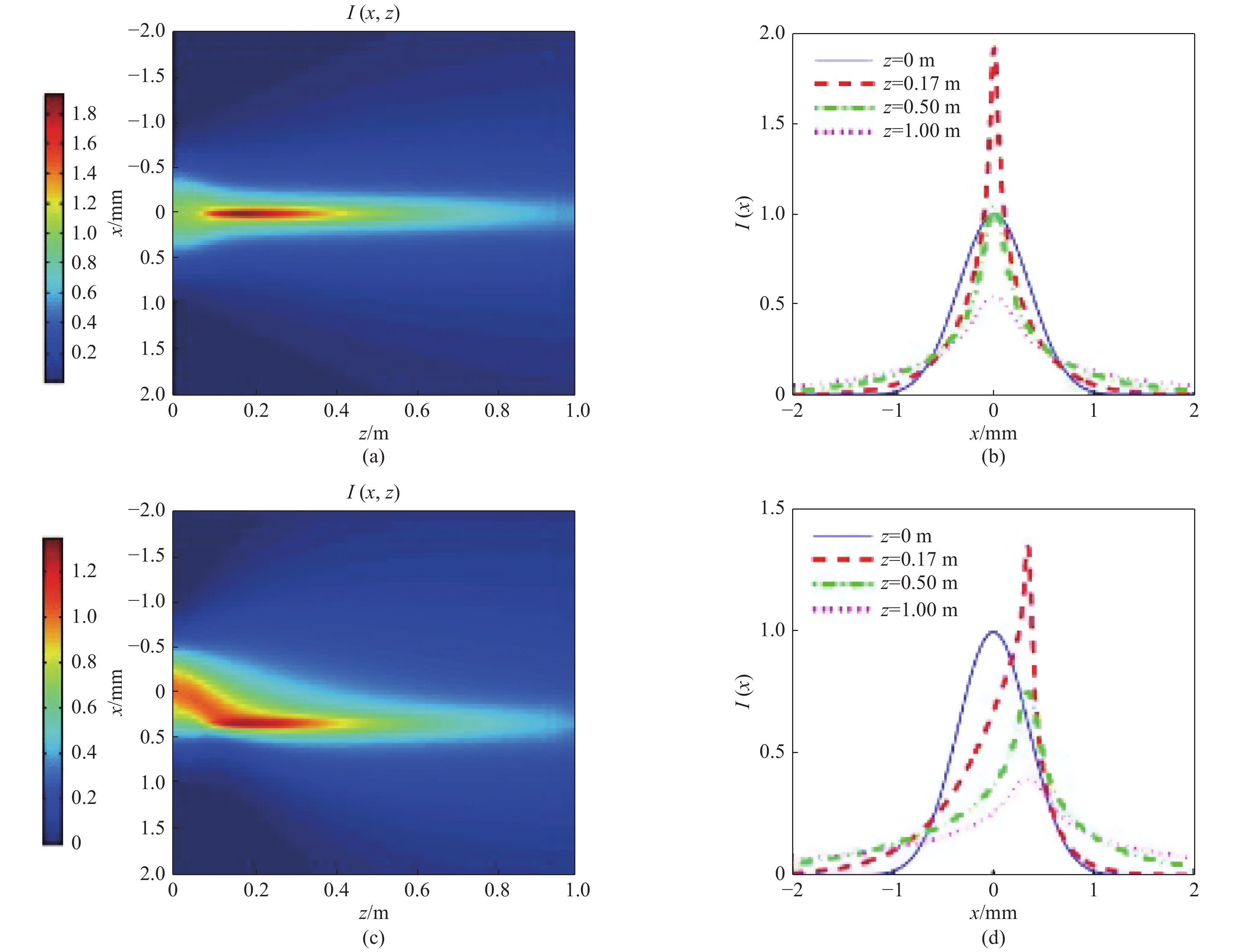
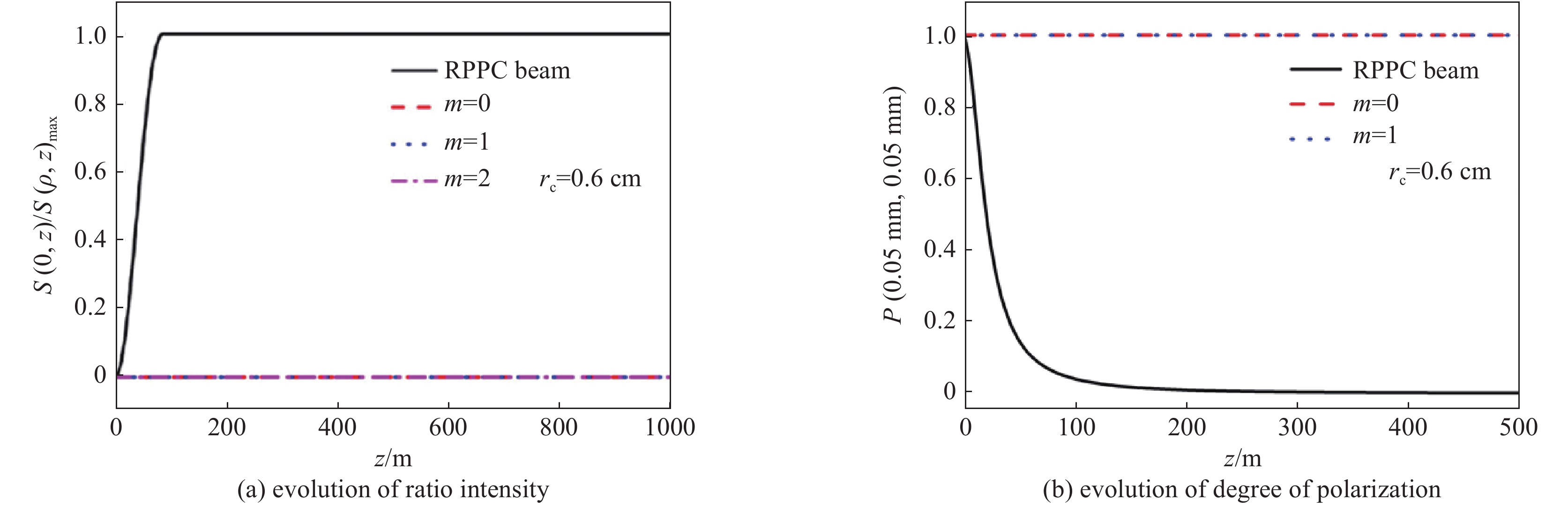
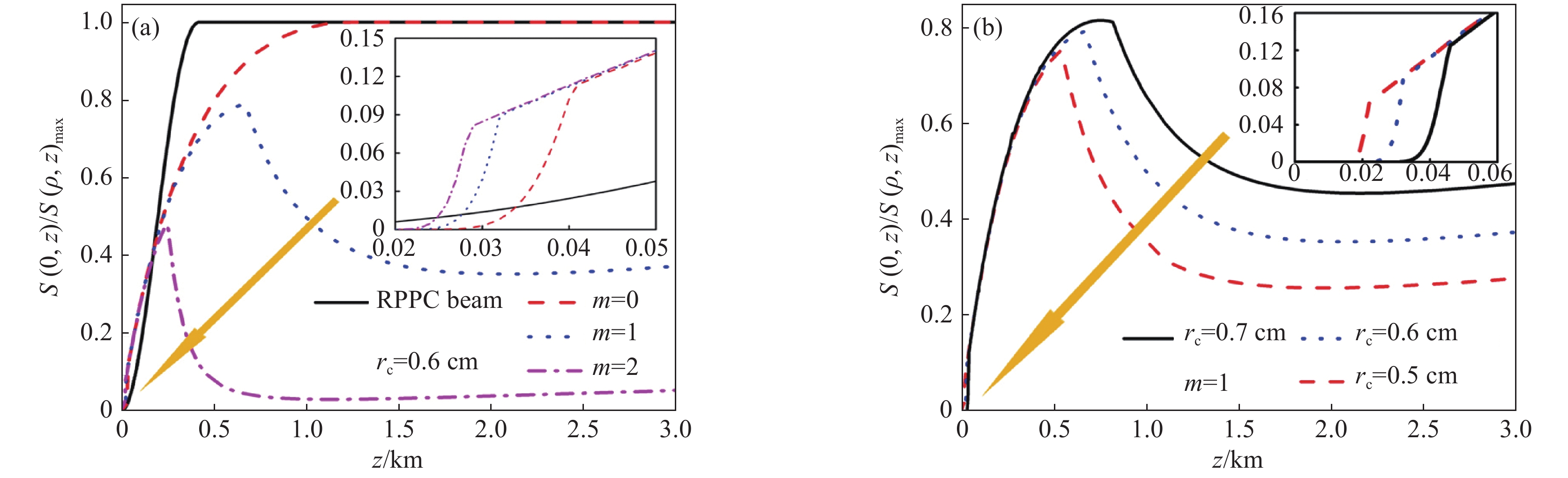
图 12 (a)传统径向偏振部分相干光束和径向偏振厄米非均匀关联结构光束不同光束阶数(b)m=0,(c)m=1的在湍流大气中的强度演化图[66]
Figure 12. Evolution of spectral intensity of (a) conventional radially polarized partially coherent beams and radially polarized Hermite non-uniform correlation beams with different mode orders (b) m=0 (c) m=1 in turbulent atmosphere[66]
-
[1] Baumgartl J, Mazilu M, Dholakia K. Optically mediated particle clearing using Airy wavepackets[J]. Nature Photonics, 2008, 2(11): 675-678. doi: 10.1038/nphoton.2008.201 [2] Garcés-Chávez V, McGloin D, Melville H, et al. Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam[J]. Nature, 2002, 419(6903): 145-147. doi: 10.1038/nature01007 [3] Lavery M P J, Speirits F C, Barnett S M, et al. Detection of a spinning object using light’s orbital angular momentum[J]. Science, 2013, 341(6145): 537-540. doi: 10.1126/science.1239936 [4] Qiao Zhen, Wan Zhenyu, Xie Guoqiang, et al. Multi-vortex laser enabling spatial and temporal encoding[J]. PhotoniX, 2020, 1: 13. doi: 10.1186/s43074-020-00013-x [5] Andrews L C, Phillips R L. Laser beam propagation through random media[M]. 2nd ed. Bellingham: SPIE Press, 2005. [6] Wolf E. Unified theory of coherence and polarization of random electromagnetic beams[J]. Physics Letters A, 2003, 312(5/6): 263-267. [7] Wolf E. Introduction to the theory of coherence and polarization of light[M]. Cambridge: Cambridge University Press, 2007. [8] Gbur G J. Singular optics[M]. Florida: CRC Press, 2016. [9] Korotkova O. Random light beams: theory and applications[M]. Florida: CRC Press, 2013. [10] Mandel L, Wolf E. Optical coherence and quantum optics[M]. Cambridge: Cambridge University Press, 1995. [11] Cai Yangjian, Chen Yahong, Yu Jiayi, et al. Chapter three—generation of partially coherent beams[J]. Progress in Optics, 2017, 62: 157-223. [12] Mitchell M, Chen Zhigang, Shih M F, et al. Self-trapping of partially spatially incoherent light[J]. Physical Review Letters, 1996, 77(3): 490-493. doi: 10.1103/PhysRevLett.77.490 [13] Akhmediev N, Królikowski W, Snyder A W. Partially coherent solitons of variable shape[J]. Physical Review Letters, 1998, 81(21): 4632-4635. doi: 10.1103/PhysRevLett.81.4632 [14] Paganin D, Nugent K A. Noninterferometric phase imaging with partially coherent light[J]. Physical Review Letters, 1998, 80(12): 2586-2589. doi: 10.1103/PhysRevLett.80.2586 [15] Clark J N, Huang X, Harder R, et al. High-resolution three-dimensional partially coherent diffraction imaging[J]. Nature Communications, 2012, 3: 993. doi: 10.1038/ncomms1994 [16] Zhang Jingfang, Wang Zhaoying, Cheng Bing, et al. Atom cooling by partially spatially coherent lasers[J]. Physical Review A, 2013, 88: 023416. doi: 10.1103/PhysRevA.88.023416 [17] Zhu Shijun, Wang Jing, Liu Xianlong, et al. Generation of arbitrary radially polarized array beams by manipulating correlation structure[J]. Applied Physics Letters, 2016, 109: 161904. doi: 10.1063/1.4965705 [18] Chen Yahong, Ponomarenko S A, Cai Yangjian. Experimental generation of optical coherence lattices[J]. Applied Physics Letters, 2016, 109: 061107. doi: 10.1063/1.4960966 [19] Liang Chunhao, Wu Gaofeng, Wang Fei, et al. Overcoming the classical Rayleigh diffraction limit by controlling two-point correlations of partially coherent light sources[J]. Optics Express, 2017, 25(23): 28352-28362. doi: 10.1364/OE.25.028352 [20] Lu Xingyuan, Shao Yifeng, Zhao Chengliang, et al. Noniterative spatially partially coherent diffractive imaging using pinhole array mask[J]. Advanced Photonics, 2019, 1: 016005. [21] Chen Yahong, Norrman A, Ponomarenko S A, et al. Chapter five—optical coherence and electromagnetic surface waves[J]. Progress in Optics, 2020, 65: 105-172. [22] Peng Deming, Huang Zhaofeng, Liu Yonglei, et al. Optical coherence encryption with structured random light[J]. PhotoniX, 2021, 2: 6. doi: 10.1186/s43074-021-00027-z [23] Lin Rong, Chen Mengyu, Liu Yonglei, et al. Measuring refractive indices of a uniaxial crystal by structured light with non-uniform correlation[J]. Optics Letters, 2021, 46(10): 2268-2271. doi: 10.1364/OL.424259 [24] Korotkova O, Gbur G. Chapter four—applications of optical coherence theory[J]. Progress in Optics, 2020, 65: 43-104. [25] Gbur G. Partially coherent beam propagation in atmospheric turbulence[J]. Journal of the Optical Society of America A, 2014, 31(9): 2038-2045. doi: 10.1364/JOSAA.31.002038 [26] Wang Fei, Liu Xianlong, Cai Yangjian. Propagation of partially coherent beam in turbulent atmosphere: a review[J]. Progress in Electromagnetics Research, 2015, 150: 123-143. doi: 10.2528/PIER15010802 [27] 王飞, 余佳益, 刘显龙, 等. 部分相干光束经过湍流大气传输研究进展[J]. 物理学报, 2018, 67:184203. (Wang Fei, Yu Jiayi, Liu Xianlong, et al. Research progress of partially coherent beams propagation in turbulent atmosphere[J]. Acta Physica Sinica, 2018, 67: 184203 doi: 10.7498/aps.67.20180877 [28] Gbur G, Wolf E. Spreading of partially coherent beams in random media[J]. Journal of the Optical Society of America A, 2002, 19(8): 1592-1598. doi: 10.1364/JOSAA.19.001592 [29] Shirai T, Dogariu A, Wolf E. Mode analysis of spreading of partially coherent beams propagating through atmospheric turbulence[J]. Journal of the Optical Society of America A, 2003, 20(6): 1094-1102. doi: 10.1364/JOSAA.20.001094 [30] Dogariu A, Amarande S. Propagation of partially coherent beams: turbulence-induced degradation[J]. Optics Letters, 2003, 28(1): 10-12. doi: 10.1364/OL.28.000010 [31] Ricklin J C, Davidson F M. Atmospheric optical communication with a Gaussian Schell beam[J]. Journal of the Optical Society of America A, 2003, 20(5): 856-866. doi: 10.1364/JOSAA.20.000856 [32] Dan Youquan, Zhang Bin. Beam propagation factor of partially coherent flat-topped beams in a turbulent atmosphere[J]. Optics Express, 2008, 16(20): 15563-15575. doi: 10.1364/OE.16.015563 [33] Dan Youquan, Zhang Bin. Second moments of partially coherent beams in atmospheric turbulence[J]. Optics Letters, 2009, 34(5): 563-565. doi: 10.1364/OL.34.000563 [34] Gu Yalong, Gbur G. Scintillation of pseudo-Bessel correlated beams in atmospheric turbulence[J]. Journal of the Optical Society of America A, 2010, 27(12): 2621-2629. doi: 10.1364/JOSAA.27.002621 [35] Cang Ji, Fang Xu, Liu Xu. Propagation properties of multi-Gaussian Schell-model beams through ABCD optical systems and in atmospheric turbulence[J]. Optics & Laser Technology, 2013, 50: 65-70. [36] Du Shengcai, Yuan Yangsheng, Liang Chunhao, et al. Second-order moments of a multi-Gaussian Schell-model beam in a turbulent atmosphere[J]. Optics & Laser Technology, 2013, 50: 14-19. [37] Yuan Yangsheng, Liu Xianlong, Wang Fei, et al. Scintillation index of a multi-Gaussian Schell-model beam in turbulent atmosphere[J]. Optics Communications, 2013, 305: 57-65. doi: 10.1016/j.optcom.2013.04.076 [38] Korotkova O, Avramov-Zamurovic S, Nelson C, et al. Scintillation reduction in multi-Gaussian Schell-model beams propagating in atmospheric turbulence[C]//Proceedings of SPIE 9224 Laser Communication and Propagation through the Atmosphere and Oceans III. 2014: 92240M. [39] Sharifi M, Wu Guohua, Luo Bin, et al. Beam wander of electromagnetic partially coherent flat-topped beam propagating in turbulent atmosphere[J]. Optik, 2014, 125(1): 561-564. doi: 10.1016/j.ijleo.2013.07.025 [40] Korotkova O, Shchepakina E. Rectangular multi-Gaussian Schell-model beams in atmospheric turbulence[J]. Journal of Optics, 2014, 16: 045704. doi: 10.1088/2040-8978/16/4/045704 [41] Wu Guohua, Zhou He, Zhao Tonggang, et al. Propagation properties of electromagnetic multi-Gaussian Schell model beams propagating through atmospheric turbulence[J]. Journal of the Korean Physical Society, 2014, 64(6): 826-831. doi: 10.3938/jkps.64.826 [42] Mei Zhangrong, Shchepakina E, Korotkova O. Propagation of cosine-Gaussian-correlated Schell-model beams in atmospheric turbulence[J]. Optics Express, 2013, 21(15): 17512-17519. doi: 10.1364/OE.21.017512 [43] Mei Zhangrong, Korotkova O. Electromagnetic cosine-Gaussian Schell-model beams in free space and atmospheric turbulence[J]. Optics Express, 2013, 21(22): 27246-27259. doi: 10.1364/OE.21.027246 [44] Xu Huafeng, Zhang Zhou, Qu Jun, et al. Propagation factors of cosine-Gaussian-correlated Schell-model beams in non-Kolmogorov turbulence[J]. Optics Express, 2014, 22(19): 22479-22489. doi: 10.1364/OE.22.022479 [45] Cang Ji, Xiu Peng, Liu Xu. Propagation of Laguerre–Gaussian and Bessel–Gaussian Schell-model beams through paraxial optical systems in turbulent atmosphere[J]. Optics & Laser Technology, 2013, 54: 35-41. [46] Wang Haiyan, Wang Hailin, Xu Yongxiang, et al. Intensity and polarization properties of the partially coherent Laguerre–Gaussian vector beams with vortices propagating through turbulent atmosphere[J]. Optics & Laser Technology, 2014, 56: 1-6. [47] Chen Rong, Liu Lin, Zhu Shijun, et al. Statistical properties of a Laguerre-Gaussian Schell-model beam in turbulent atmosphere[J]. Optics Express, 2014, 22(2): 1871-1883. doi: 10.1364/OE.22.001871 [48] Yu Jiayi, Chen Yahong, Liu Lin, et al. Splitting and combining properties of an elegant Hermite-Gaussian correlated Schell-model beam in Kolmogorov and non-Kolmogorov turbulence[J]. Optics Express, 2015, 23(10): 13467-13481. doi: 10.1364/OE.23.013467 [49] Zhou Yuan, Yuan Yangsheng, Qu Jun, et al. Propagation properties of Laguerre-Gaussian correlated Schell-model beam in non-Kolmogorov turbulence[J]. Optics Express, 2016, 24(10): 10682-10693. doi: 10.1364/OE.24.010682 [50] 余佳益, 陈亚红, 蔡阳健. 非均匀拉盖尔-高斯关联光束及其传输特性[J]. 物理学报, 2016, 65:214202. (Yu Jiayi, Chen Yahong, Cai Yangjian. Nonuniform Laguerre-Gaussian correlated beam and its propagation properties[J]. Acta Physica Sinica, 2016, 65: 214202 doi: 10.7498/aps.65.214202 [51] Liu Xianlong, Yu Jiayi, Cai Yangjian, et al. Propagation of optical coherence lattices in the turbulent atmosphere[J]. Optics Letters, 2016, 41(18): 4182-4185. doi: 10.1364/OL.41.004182 [52] Peng Xiaofeng, Liu Lin, Yu Jiayi, et al. Propagation of a radially polarized twisted Gaussian Schell-model beam in turbulent atmosphere[J]. Journal of Optics, 2016, 18: 125601. doi: 10.1088/2040-8978/18/12/125601 [53] Xu Yonggen, Dan Youquan, Yu Jiayi, et al. Propagation properties of partially coherent dark hollow beam in inhomogeneous atmospheric turbulence[J]. Journal of Modern Optics, 2016, 63(21): 2186-2197. doi: 10.1080/09500340.2016.1187308 [54] Song Zhenzhen, Liu Zhengjun, Zhou Keya, et al. Propagation factors of multi-sinc Schell-model beams in non-Kolmogorov turbulence[J]. Optics Express, 2016, 24(2): 1804-1813. doi: 10.1364/OE.24.001804 [55] Li Jinhong, Suo Qiangbo, Chen Linying. Analysis to beam quality of partially coherent flat-topped vortex beams propagating through atmospheric turbulence[J]. Optik, 2016, 127(23): 11342-11348. doi: 10.1016/j.ijleo.2016.09.031 [56] Zhu Jie, Li Xiaoli, Tang Huiqin, et al. Propagation of multi-cosine-Laguerre-Gaussian correlated Schell-model beams in free space and atmospheric turbulence[J]. Optics Express, 2017, 25(17): 20071-20086. doi: 10.1364/OE.25.020071 [57] Xu Yonggen, Dan Youquan, Yu Jiayi, et al. Kurtosis parameter K of arbitrary electromagnetic beams propagating through non-Kolmogorov turbulence[J]. Journal of Modern Optics, 2017, 64(19): 1976-1987. doi: 10.1080/09500340.2017.1330974 [58] Yu Jiayi, Cai Yangjian, Gbur G. Rectangular Hermite non-uniformly correlated beams and its propagation properties[J]. Optics Express, 2018, 26(21): 27894-27906. doi: 10.1364/OE.26.027894 [59] Yu Jiayi, Wang Fei, Liu Lin, et al. Propagation properties of Hermite non-uniformly correlated beams in turbulence[J]. Optics Express, 2018, 26(13): 16333-16343. doi: 10.1364/OE.26.016333 [60] Huang Yan, Yuan Yangsheng, Liu Xianlong, et al. Propagation of optical coherence vortex lattices in turbulent atmosphere[J]. Applied Sciences, 2018, 8: 2476. doi: 10.3390/app8122476 [61] Yu Jiayi, Zhu Xinlei, Wang Fei, et al. Experimental study of reducing beam wander by modulating the coherence structure of structured light beams[J]. Optics Letters, 2019, 44(17): 4371-4374. doi: 10.1364/OL.44.004371 [62] Yu Jiayi, Huang Yan, Wang Fei, et al. Scintillation properties of a partially coherent vector beam with vortex phase in turbulent atmosphere[J]. Optics Express, 2019, 27(19): 26676-26688. doi: 10.1364/OE.27.026676 [63] Lin Rong, Yu Hancheng, Zhu Xinlei, et al. The evolution of spectral intensity and orbital angular momentum of twisted Hermite Gaussian Schell model beams in turbulence[J]. Optics Express, 2020, 28(5): 7152-7164. doi: 10.1364/OE.387443 [64] Zhang Bo, Huang Hongkun, Xie Chenxia, et al. Twisted rectangular Laguerre–Gaussian correlated sources in anisotropic turbulent atmosphere[J]. Optics Communications, 2020, 459: 125004. doi: 10.1016/j.optcom.2019.125004 [65] Wei Dongmei, Li Shuwei, Zeng Jun, et al. Comparative study of spiral spectrum of elegant and standard Laguerre–Gaussian beams in atmospheric turbulence[J]. Journal of Russian Laser Research, 2020, 41(4): 364-372. doi: 10.1007/s10946-020-09887-5 [66] Lin Shuqin, Wang Cong, Zhu Xinlei, et al. Propagation of radially polarized Hermite non-uniformly correlated beams in a turbulent atmosphere[J]. Optics Express, 2020, 28(19): 27238-27249. doi: 10.1364/OE.402021 [67] Zhao Xuechun, Zhang Lei, Lin Rong, et al. Hermite non-uniformly correlated array beams and its propagation properties[J]. Chinese Physics Letters, 2020, 37: 124202. doi: 10.1088/0256-307X/37/12/124202 [68] Liu Yonglei, Lin Rong, Wang Fei, et al. Propagation properties of Laguerre-Gaussian Schell-model beams with a twist phase[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2021, 264: 107556. doi: 10.1016/j.jqsrt.2021.107556 [69] Cai Yangjian, Chen Yahong, Wang Fei. Generation and propagation of partially coherent beams with nonconventional correlation functions: a review [Invited][J]. Journal of the Optical Society of America A, 2014, 31(9): 2083-2096. doi: 10.1364/JOSAA.31.002083 [70] Gori F, Santarsiero M. Devising genuine spatial correlation functions[J]. Optics Letters, 2007, 32(24): 3531-3533. doi: 10.1364/OL.32.003531 [71] Gori F, Ramírez-Sánchez V, Santarsiero M, et al. On genuine cross-spectral density matrices[J]. Journal of Optics A: Pure and Applied Optics, 2009, 11: 085706. doi: 10.1088/1464-4258/11/8/085706 [72] Monin A S, Yaglom A M, Lumley J L. Statistical fluid mechanics: mechanics of turbulence[M]. Cambridge: The MIT Press, 1971. [73] Taylor G I. The spectrum of turbulence[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1938, 164(919): 476-490. doi: 10.1098/rspa.1938.0032 [74] Kolmogorov A N. The local structure of turbulence in an incompressible fluid at very high Reynolds number[J]. Soviet Physics Uspekhi, 1941, 30(4): 301-305. [75] Born M, Wolf E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light[M]. 7th ed. Cambridge: Cambridge University Press, 1999. [76] Tatarskiĭ V I. Wave propagation in a turbulent medium[M]. New York: McGraw-Hill, 1961. [77] Harlow G R. Wave propagation in a random medium[J]. Physics Bulletin, 1960, 11(9): 232-233. [78] Lutomirski R F, Yura H T. Propagation of a finite optical beam in an inhomogeneous medium[J]. Applied Optics, 1971, 10(7): 1652-1658. doi: 10.1364/AO.10.001652 [79] Yura H T, Hanson S G. Second-order statistics for wave propagation through complex optical systems[J]. Journal of the Optical Society of America A, 1989, 6(4): 564-575. doi: 10.1364/JOSAA.6.000564 [80] Siegman A E. New developments in laser resonators[C]//Proceedings of SPIE, Optical Resonators. 1990, 1224:2-4. [81] Sahin S, Korotkova O. Light sources generating far fields with tunable flat profiles[J]. Optics Letters, 2012, 37(14): 2970-2972. doi: 10.1364/OL.37.002970 [82] Korotkova O, Sahin S, Shchepakina E. Multi-Gaussian Schell-model beams[J]. Journal of the Optical Society of America A, 2012, 29(10): 2159-2164. doi: 10.1364/JOSAA.29.002159 [83] Chen Yahong, Gu Jiaxin, Wang Fei, et al. Self-splitting properties of a Hermite-Gaussian correlated Schell-model beam[J]. Physical Review A, 2015, 91: 013823. doi: 10.1103/PhysRevA.91.013823 [84] Wang Fei, Liu Xianlong, Yuan Yangsheng, et al. Experimental generation of partially coherent beams with different complex degrees of coherence[J]. Optics Letters, 2013, 38(11): 1814-1816. doi: 10.1364/OL.38.001814 [85] Wang Fei, Liang Chunhao, Yuan Yangsheng, et al. Generalized multi-Gaussian correlated Schell-model beam: from theory to experiment[J]. Optics Express, 2014, 22(19): 23456-23464. doi: 10.1364/OE.22.023456 [86] Chen Yahong, Liu Lin, Wang Fei, et al. Elliptical Laguerre-Gaussian correlated Schell-model beam[J]. Optics Express, 2014, 22(11): 13975-13987. doi: 10.1364/OE.22.013975 [87] Chen Yahong, Wang Fei, Zhao Chengliang, et al. Experimental demonstration of a Laguerre-Gaussian correlated Schell-model vortex beam[J]. Optics Express, 2014, 22(5): 5826-5838. doi: 10.1364/OE.22.005826 [88] Liang Chunhao, Wang Fei, Liu Xianlong, et al. Experimental generation of cosine-Gaussian-correlated Schell-model beams with rectangular symmetry[J]. Optics Letters, 2014, 39(4): 769-772. doi: 10.1364/OL.39.000769 [89] Chen Yahong, Wang Fei, Liu Lin, et al. Generation and propagation of a partially coherent vector beam with special correlation functions[J]. Physical Review A, 2014, 89: 013801. doi: 10.1103/PhysRevA.89.013801 [90] Zhu Shijun, Chen Yahong, Wang Jing, et al. Generation and propagation of a vector cosine-Gaussian correlated beam with radial polarization[J]. Optics Express, 2015, 23(26): 33099-33115. doi: 10.1364/OE.23.033099 [91] Chen Yahong, Yu Jiayi, Yuan Yangsheng, et al. Theoretical and experimental studies of a rectangular Laguerre–Gaussian-correlated Schell-model beam[J]. Applied Physics B, 2016, 122: 31. [92] Peng Xiaofeng, Lu Xingyuan, Liu Xianlong, et al. Generation and propagation of a Hermite-Gaussian correlated Schell-model LG0l beam[J]. Applied Sciences, 2019, 9: 610. doi: 10.3390/app9030610 [93] Hyde IV M W, Basu S, Voelz D G, et al. Experimentally generating any desired partially coherent Schell-model source using phase-only control[J]. Journal of Applied Physics, 2015, 118: 093102. doi: 10.1063/1.4929811 [94] Hyde IV M W, Basu S, Voelz D G, et al. Generating partially coherent Schell-model sources using a modified phase screen approach[J]. Optical Engineering, 2015, 54: 120501. doi: 10.1117/1.OE.54.12.120501 [95] Lajunen H, Saastamoinen T. Propagation characteristics of partially coherent beams with spatially varying correlations[J]. Optics Letters, 2011, 36(20): 4104-4106. doi: 10.1364/OL.36.004104 [96] Tong Zhisong, Korotkova O. Nonuniformly correlated light beams in uniformly correlated media[J]. Optics Letters, 2012, 37(15): 3240-3242. doi: 10.1364/OL.37.003240 [97] Gu Yalong, Gbur G. Scintillation of nonuniformly correlated beams in atmospheric turbulence[J]. Optics Letters, 2013, 38(9): 1395-1397. doi: 10.1364/OL.38.001395 [98] Yu Jiayi, Zhu Xinlei, Lin Shuqin, et al. Vector partially coherent beams with prescribed non-uniform correlation structure[J]. Optics Letters, 2020, 45(13): 3824-3827. doi: 10.1364/OL.397316 [99] Hyde IV M W, Bose-Pillai S, Voelz D G, et al. Generation of vector partially coherent optical sources using phase-only spatial light modulators[J]. Physical Review Applied, 2016, 6: 064030. doi: 10.1103/PhysRevApplied.6.064030 [100] Hyde IV M W, Bose-Pillai S R, Wood R A. Synthesis of non-uniformly correlated partially coherent sources using a deformable mirror[J]. Applied Physics Letters, 2017, 111: 101106. doi: 10.1063/1.4994669 [101] Zhu Xinlei, Yu Jiayi, Wang Fei, et al. Synthesis of vector nonuniformly correlated light beams by a single digital mirror device[J]. Optics Letters, 2021, 46(12): 2996-2999. doi: 10.1364/OL.428508 -





 下载:
下载: