Study on preheating ablative effects of two-mode Rayleigh-Taylor instability
-
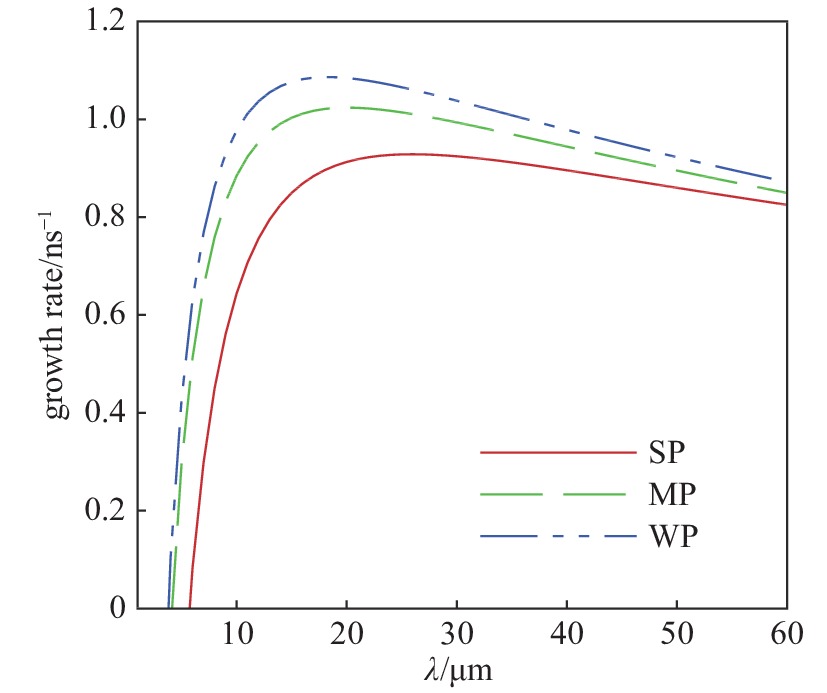
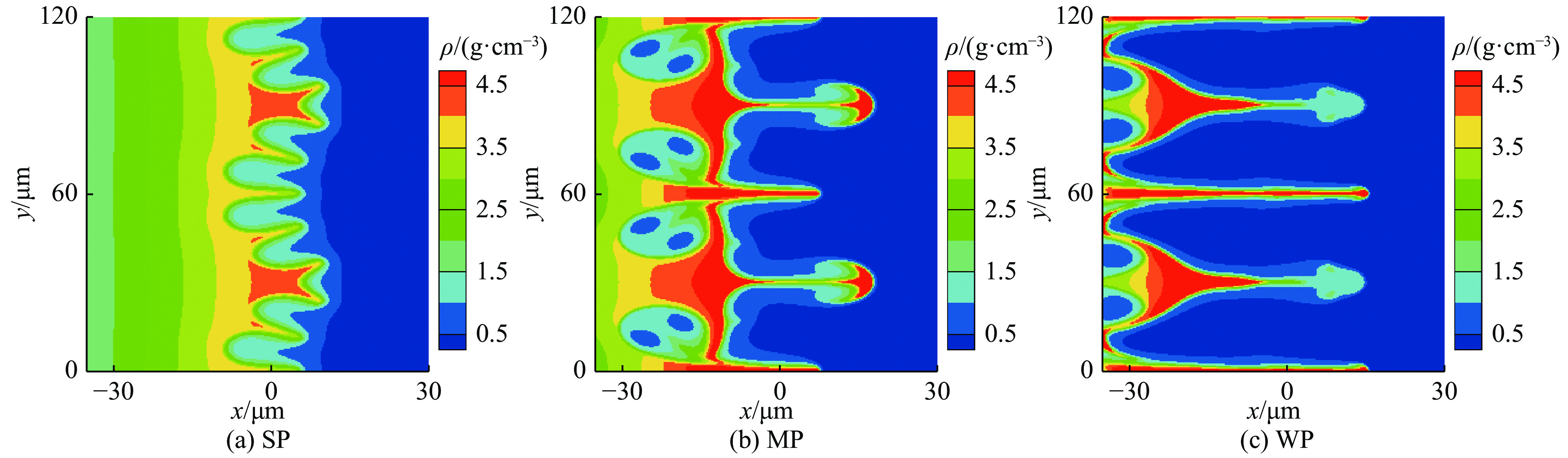
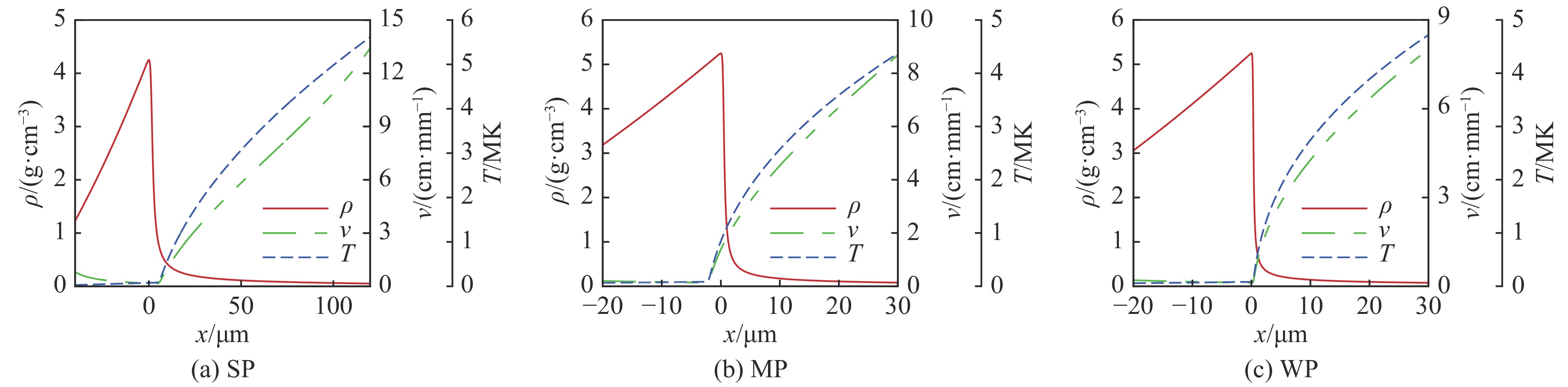
摘要: 针对双模扰动下的烧蚀瑞利-泰勒不稳定性增长问题,采用高精度的数值计算方法,研究了不同预热程度下模耦合产生的多个高次谐波幅值的发展和演化问题。研究表明,三种预热烧蚀条件下,当扰动基模满足长波与短波耦合方式时,谐波中的长波模态占主导,而短波模发展明显受到抑制;当满足短波与短波耦合时,耦合结果带来了许多新的增长较快的长波模态,此时短波模增长呈现小幅震荡形式。比较两种耦合方式可以发现,长波结构在烧蚀瑞利-泰勒不稳定性弱非线性阶段都占主导地位,尤其是短波与短波耦合中气泡与尖钉表现出不同于两个基模的长波模结构。进一步分析预热效应对模耦合增长的影响,发现预热程度越强就越能削弱耦合谐波的增长,这说明预热对烧蚀瑞利-泰勒不稳定性具有致稳作用,这对惯性约束聚变工程中控制烧蚀瑞利-泰勒不稳定性发展具有重要意义。Abstract: Aiming at the growth of ablative Rayleigh-Taylor instability with two perturbations, the evolutions of the amplitudes of high-order harmonics excited by two-mode coupling under different preheating conditions are studied by using a high-precision numerical simulation method. When the fundamental modes are a long-wavelength and a short-wavelength mode, the long-wavelength modes of the excited harmonics are dominant, while the development of short-wavelength modes are obviously suppressed; when the fundamental modes are two short-wavelength modes, many fast-growing and long-wavelength modes are excited, and the growth of short-wavelength modes are in the form of small oscillation. By comparing the two different two-mode coupling cases, it is found that the long-wavelength structures are dominant in the weakly nonlinear stage. Especially, in the two short-wavelength modes coupling case, the bubbles and spikes show long-wavelength structures which are different from the two fundamental modes. By further comparing the three preheating ablative effects, it is found that the higher the preheat degree is, the more the coupled harmonics growth will be weakened. It is of great significance to control the development of ablative Rayleigh-Taylor instability in inertial confinement fusion engineering.
-
Key words:
- two-mode perturbations /
- preheating /
- Rayleigh-Taylor instability /
- high-order harmonics /
- bubbles /
- spikes
-
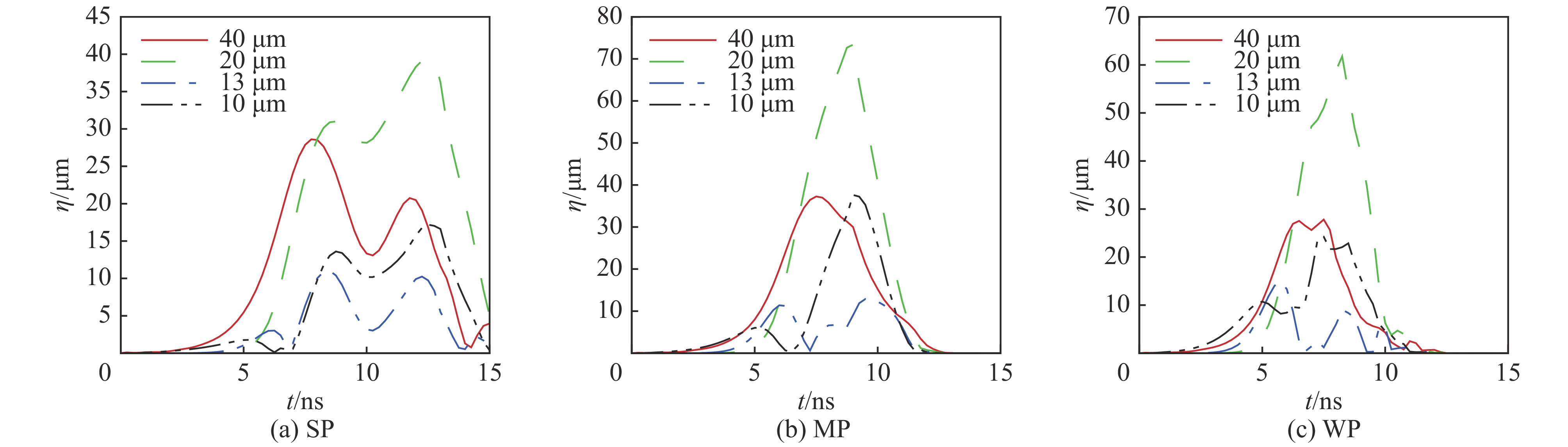
图 3 不同预热情况下
$ {\lambda }_{1}=10\;{\text{μ}}\rm{m} $ 与$ {\lambda }_{2}=40\;{\text{μ}}\rm{m} $ 双模扰动所激发的谐波的密度幅值随时间的演化Figure 3. Temporal evolution of the density amplitude of harmonics excited by the coupling of two modes (short-and long-wavelength
$ {\lambda }_{1}=10\;{\text{μ}}\rm{m} $ and$ {\lambda }_{2}=40\;{\text{μ}}\rm{m} $ ) in different preheating cases图 5 不同预热情况下
$ {\lambda }_{1}=10\;{\text{μ}}\rm{m} $ 与$ {\lambda }_{2}=12\;{\text{μ}}\rm{m} $ 双模扰动所激发的谐波的密度幅值随时间的演化Figure 5. Temporal evolution of the density amplitude of harmonics excited by the coupling of two short-wavelength modes (
$ {\lambda }_{1}=10\;{\text{μ}}\rm{m} $ and$ {\lambda }_{2}=12\;{\text{μ}}\rm{m} $ ) in different preheating cases表 1 三种预热条件的参数设置
Table 1. Parameter settings of strong, medium and weak preheating conditions
case b c strong preheating (SP) 8.6 1.6 moderate preheating (MP) 2 0.4 weak preheating (WP) 0.86 0.24 -
[1] Taylor G I. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I[J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1950, 201(1065): 192-196. [2] Strutt J W. ART. 100—Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density[M]//Strutt J W. Scientific Papers. Cambridge: Cambridge University Press, 1900: 200-207. [3] Sharp D H. An overview of Rayleigh-Taylor instability[J]. Physica D: Nonlinear Phenomena, 1984, 12(1/3): 3-18. [4] Bodner S E. Rayleigh-Taylor instability and laser-pellet fusion[J]. Physical Review Letters, 1974, 33(13): 761-764. doi: 10.1103/PhysRevLett.33.761 [5] Nuckolls J, Wood L, Thiessen A, et al. Laser compression of matter to super-high densities: thermonuclear (CTR) application[J]. Nature, 1972, 239(5368): 139-142. doi: 10.1038/239139a0 [6] Lindl J. Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain[J]. Physics of Plasmas, 1995, 2(11): 3933-4024. doi: 10.1063/1.871025 [7] Takabe H, Mima K, Montierth L, et al. Self-consistent growth rate of the Rayleigh-Taylor instability in an ablatively accelerating plasma[J]. Physics of Fluids, 1985, 28(12): 3676. doi: 10.1063/1.865099 [8] Sanz J. Self-consistent analytical model of the Rayleigh-Taylor instability in inertial confinement fusion[J]. Physical Review E, 1996, 53(4): 4026-4045. doi: 10.1103/PhysRevE.53.4026 [9] Roberts M S, Jacobs J W. The effects of forced small-wavelength, finite-bandwidth initial perturbations and miscibility on the turbulent Rayleigh-Taylor instability[J]. Journal of Fluid Mechanics, 2016, 787: 50-83. doi: 10.1017/jfm.2015.599 [10] Zhang H, Betti R, Gopalaswamy V, et al. Nonlinear excitation of the ablative Rayleigh-Taylor instability for all wave numbers[J]. Physical Review E, 2018, 97: 011203. doi: 10.1103/PhysRevE.97.011203 [11] Zhao Kaige, Xue Chuang, Wang Lifeng, et al. Two-dimensional thin shell model for the nonlinear Rayleigh-Taylor instability in spherical geometry[J]. Physics of Plasmas, 2019, 26: 022710. doi: 10.1063/1.5079316 [12] Qiao Xiumei, Lan Ke. Novel target designs to mitigate hydrodynamic instabilities growth in inertial confinement fusion[J]. Physical Review Letters, 2021, 126: 185001. doi: 10.1103/PhysRevLett.126.185001 [13] Bud’ko A B, Liberman M A. Stabilization of the Rayleigh-Taylor instability by convection in smooth density gradient: Wentzel-Kramers-Brillouin analysis[J]. Physics of Fluids B: Plasma Physics, 1992, 4(11): 3499-3506. doi: 10.1063/1.860357 [14] Betti R, Goncharov V N, McCrory R L, et al. Growth rates of the ablative Rayleigh–Taylor instability in inertial confinement fusion[J]. Physics of Plasmas, 1998, 5(5): 1446-1454. doi: 10.1063/1.872802 [15] Lewis D J. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. II[J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1950, 202(1068): 81-96. [16] Birkhoff G. Taylor instability and laminar mixing[R]. Los Alamos: Las Alamos Scientific Lab. , 1954. [17] Birkhoff G, Bellman R, Lin C C. Hydrodynamic instability[M]. New York: Am. Math. Soc. , 1962: 55-76. [18] 张维岩, 叶文华, 吴俊峰, 等. 激光间接驱动聚变内爆流体不稳定性研究[J]. 中国科学:物理学 力学 天文学, 2014, 44(1):1-23. (Zhang Weiyan, Ye Wenhua, Wu Junfeng, et al. Hydrodynamic instabilities of laser indirect-drive inertial-confinement-fusion implosion[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2014, 44(1): 1-23Zhang Weiyan, Ye Wenhua, Wu Junfeng, et al. Hydrodynamic instabilities of laser indirect-drive inertial-confinement-fusion implosion[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2014, 44(1): 1-23 [19] Ye Wenhua, Zhang Weiyan, He Xiantu. Stabilization of ablative Rayleigh-Taylor instability due to change of the Atwood number[J]. Physical Review E, 2002, 65: 057401. doi: 10.1103/PhysRevE.65.057401 [20] 叶文华, 张维岩, 贺贤土. 烧蚀瑞利-泰勒不稳定性线性增长率的预热致稳公式[J]. 物理学报, 2000, 49(4):762-767. (Ye Wenhua, Zhang Weiyan, He Xiantu. Preheating stabilization formula of linear growth rate for ablative Rayleigh-Taylor instability[J]. Acta Physical Sinica, 2000, 49(4): 762-767 doi: 10.3321/j.issn:1000-3290.2000.04.032Ye Wenhua, Zhang Weiyan, He Xiantu. Preheating stabilization formula of linear growth rate for ablative Rayleigh-Taylor instability[J]. Acta Physical Sinica, 2000, 49(4): 762-767 doi: 10.3321/j.issn:1000-3290.2000.04.032 [21] Xia Hua, Shats M G. Spectral energy transfer and generation of turbulent structures in toroidal plasma[J]. Physics of Plasmas, 2004, 11(2): 561-571. doi: 10.1063/1.1637607 [22] Wang Lifeng, Ye Wenhua, Li Yingjun. Interface width effect on the classical Rayleigh–Taylor instability in the weakly nonlinear regime[J]. Physics of Plasmas, 2010, 17: 052305. doi: 10.1063/1.3396369 [23] Garnier J, Raviart P A, Cherfils-Clérouin C, et al. Weakly nonlinear theory for the ablative Rayleigh-Taylor instability[J]. Physical Review Letters, 2003, 90: 185003. doi: 10.1103/PhysRevLett.90.185003 [24] Verdon C P, McCrory R L, Morse R L, et al. Nonlinear effects of multifrequency hydrodynamic instabilities on ablatively accelerated thin shells[J]. Physics of Fluids, 1982, 25(9): 1653-1674. doi: 10.1063/1.863925 [25] Dahlburg J P, Gardner J H. Ablative Rayleigh-Taylor instability in three dimensions[J]. Physical Review A, 1990, 41(10): 5695-5698. doi: 10.1103/PhysRevA.41.5695 [26] Xin Jingfei, Yan Rui, Wan Zhenhua, et al. Two mode coupling of the ablative Rayleigh-Taylor instabilities[J]. Physics of Plasmas, 2019, 26: 032703. doi: 10.1063/1.5070103 [27] Hasegawa S, Nishihara K. Mode coupling theory in ablative Rayleigh-Taylor instability[J]. Physics of Plasmas, 1995, 2(12): 4606-4616. doi: 10.1063/1.870950 [28] Ye Wenhua, Wang Lifeng, He Xiantu. Spike deceleration and bubble acceleration in the ablative Rayleigh-Taylor instability[J]. Physics of Plasmas, 2010, 17: 122704. doi: 10.1063/1.3497006 [29] Fan Zhengfeng, Luo Jisheng, Ye Wenhua. Compressible Rayleigh-Taylor instability with preheat in inertial confinement fusion[J]. Chinese Physics Letters, 2007, 24(8): 2308-2311. doi: 10.1088/0256-307X/24/8/042 [30] Wang Lifeng, Ye Wenhua, He Xiantu. Density gradient effects in weakly nonlinear ablative Rayleigh-Taylor instability[J]. Physics of Plasmas, 2012, 19: 012706. doi: 10.1063/1.3677821 [31] 王立锋, 叶文华, 陈竹, 等. 激光聚变内爆流体不稳定性基础问题研究进展[J]. 强激光与粒子束, 2021, 33:012001. (Wang Lifeng, Ye Wenhua, Chen Zhu, et al. Review of hydrodynamic instabilities in inertial confinement fusion implosions[J]. High Power Laser and Particle Beams, 2021, 33: 012001 doi: 10.11884/HPLPB202132.200173Wang Lifeng, Ye Wenhua, Chen Zhu, et al. Review of hydrodynamic instabilities in inertial confinement fusion implosions[J]. High Power Laser and Particle Beams, 2021, 33: 012001 doi: 10.11884/HPLPB202132.200173 -




 下载:
下载: