Physical design of calibrated device for intense pulse electron beam position monitor
-
摘要: 从强流脉冲电子直线感应加速器电子束流位置探测器测量原理出发，进行了标定装置物理设计，确定标定装置采用同轴结构，对束流探测器位置测量精度和测量范围、偏心同轴线对位置标定结果的影响进行了理论分析，并根据分析结果确定同轴结构内外导体相对位置调节范围、同轴线长度和特性阻抗。电路模拟和实验测量结果验证了在非匹配传输条件下可以得到满足位置标定要求的快脉冲信号波形。Abstract: Accurate measurement of the intense pulse electron beam transverse position is not only related to the technology of beam position monitor (BPM) design, machining and assembly, but also related to calibration of BPM. This paper describes the physical design of the calibrated device based on the measuring principle of intense pulse electron beam position monitor in linear induction accelerator. A coaxial line structure is used as the calibrated device. The axial length that affects the electromagnetic field at a given location and the position measurement affected by coaxial line with displaced inner conductor are analyzed in theory, the results determine the length and the characteristic impedance of the coaxial line. The extent of inner conductor displacement is determined by the calculated errors of beam position measurement. Pulse signal mismatch transmission in calibration, the PSpice simulation and experimental measurement are performed, and results show that a required pulse waveform is obtained.
-
Key words:
- linear induction accelerator /
- pulsed electron beam /
- position monitor /
- calibration /
- calibrated device /
- design
-
图 2 无限长电流在范围Z内的磁场示意图
Figure 2. Sketch of axial magnetic field generated by infinite length line current
图 4 同轴线电中心与几何中心比值随特性阻抗变化
Figure 4. Ratio of electric center to geometric center vs characteristic impedance of coaxial line
图 5 理想束流探测器位置测量结果与束流位置设置结果比较
Figure 5. Compareison between measurement of ideal BPM and set position
图 7 不同标定装置特性阻抗时的脉冲波形
Figure 7. Pulse waveform in different characteristic impedance of calibrated device
图 10 脉冲信号源输出电压、电流波形
Figure 10. Output voltage and current waveform of pulse signal source
-
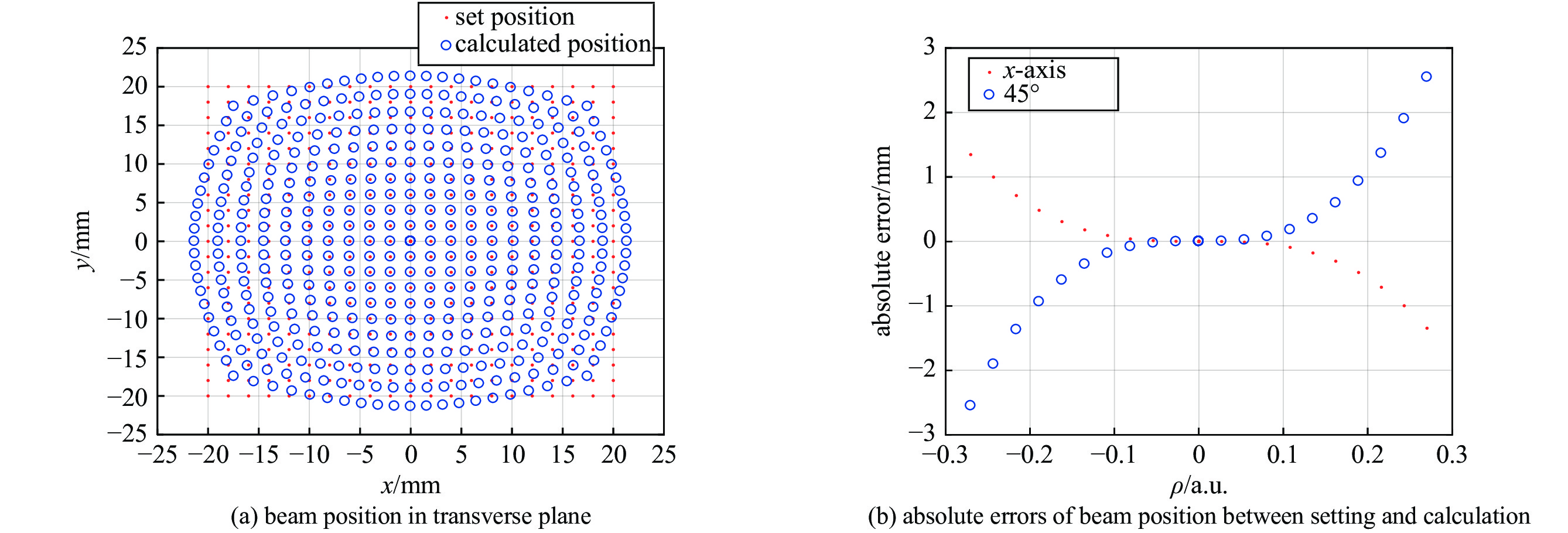
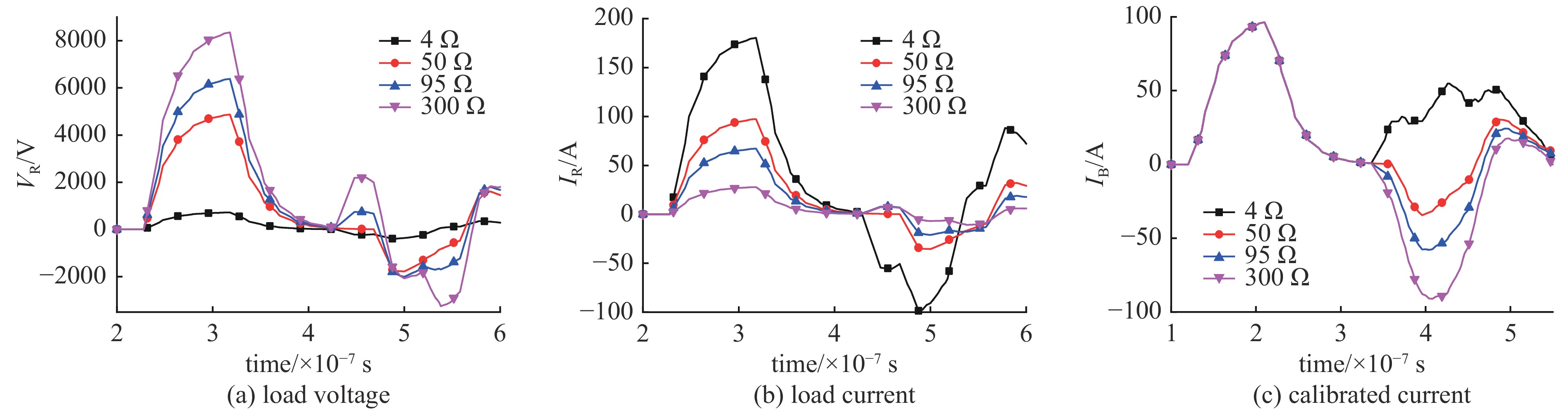
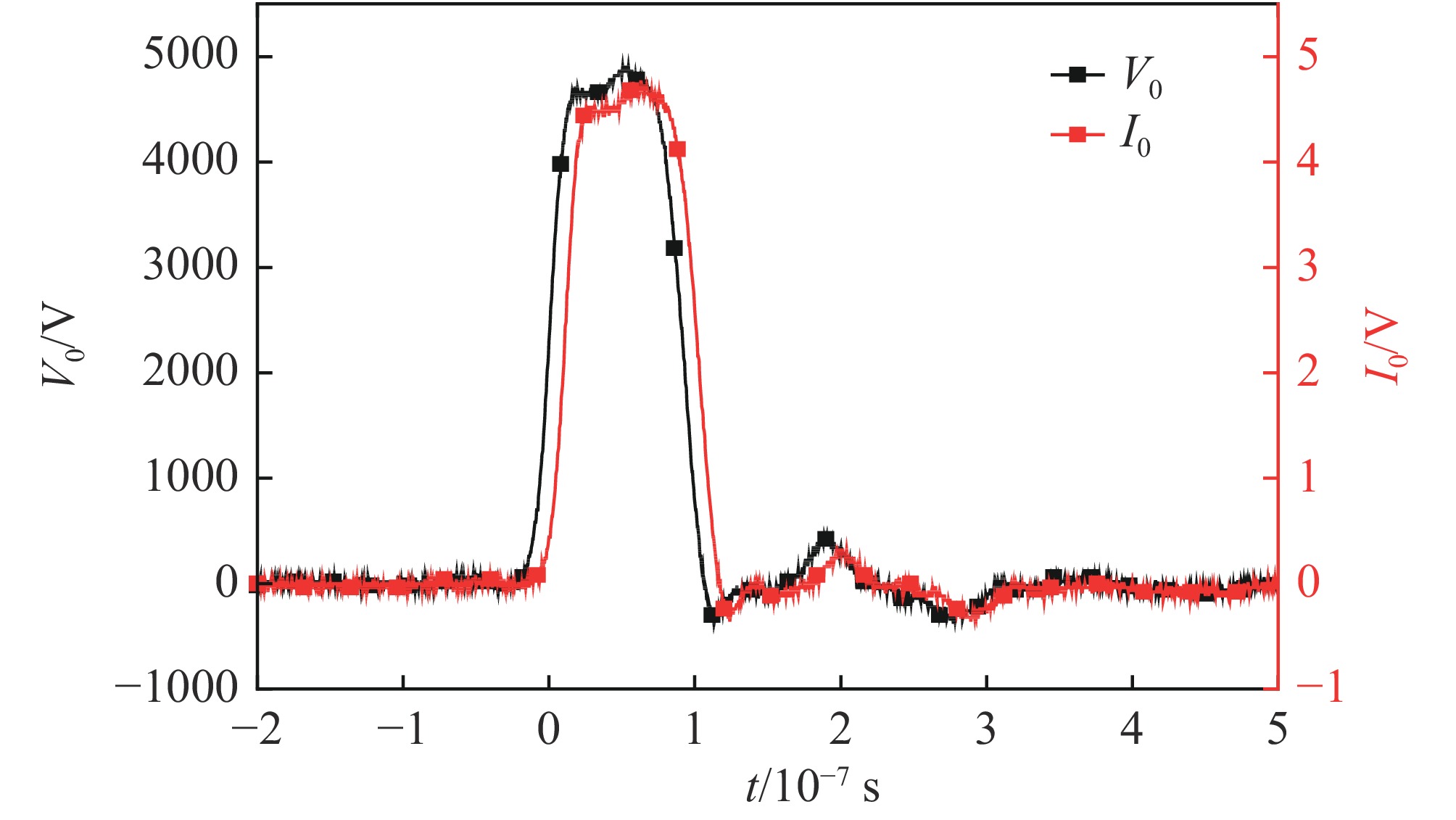
[1] 何文龙. 电阻环法模拟测量电子束流动大小和位置[C]//10 MeV直线感应加速器会议文集. 1994He Wenlong. Intensity and position measurements of an intense particle beam using resistance ring[C]//Proceedings of the conference on 10 MeV Liner Induction Accelerator. 1994 [2] Fessenden T J, Stallard B W, Berg G G. Beam current and position monitor for the Astron accelerator[J]. Review of Scientific Instruments, 1972, 43(12): 1789-1792. doi: 10.1063/1.1685566 [3] 谢宇彤, 代志勇, 韩青. 电阻环束流探测器的标定[J]. 强激光与粒子束, 2002, 14(1):151-155Xie Yutong, Dai Zhiyong, Han Qing. Improvement on the accuracy of beam bugs in linear induction accelerator[J]. High Power Laser and Particle Beams, 2002, 14(1): 151-155 [4] 李勤, 李洪, 陈楠, 等. 用于测量强流脉冲电子束的B-dot[J]. 强激光与粒子束, 2009, 21(9):1390-1394Li Qin, Li Hong, Chen Nan, et al. B-dot monitor for intense electron beam measurement[J]. High Power Laser and Particle Beams, 2009, 21(9): 1390-1394 [5] 赵籍九, 尹兆升. 粒子加速器技术[M]. 北京: 高等教育出版社, 2006Zhao Jijiu, Yin Zhaosheng. Particle accelerator technology[M]. Beijing: Higher Education Press, 2006 [6] 王盛昌, 王安鑫, 徐韬光. 用于质子加速器的壁电流探头的研制[J]. 强激光与粒子束, 2012, 24(9):2179-2182 doi: 10.3788/HPLPB20122409.2179Wang Shengchang, Wang Anxin, Xu Taoguang. Design of wall current monitor for proton accelerators[J]. High Power Laser and Particle Beams, 2012, 24(9): 2179-2182 doi: 10.3788/HPLPB20122409.2179 [7] 邹俊颖. HLS ΙΙ 注入器束流位置测量系统的研制及应用研究[D]. 合肥: 中国科学技术大学, 2014Zou Junying. Development and application of injector beam position monitor system at HLS ΙΙ[D]. Hefei: University of Science and Technology of China, 2014 [8] 王建新, 刘宇, 张浩, 等. 积分式束流变压器的标定研究[J]. 原子能科学技术, 2015, 49(s1):620-623 doi: 10.7538/yzk.2015.49.S1.0620Wang Jianxin, Liu Yu, Zhang Hao, et al. Calibration of integrating current transformer[J]. Atomic Energy Science and Technology, 2015, 49(s1): 620-623 doi: 10.7538/yzk.2015.49.S1.0620 [9] 李吉浩, 孙葆根, 何多慧, 等. HLS 直线加速器条带束流位置检测器基于对数比方法的标定[J]. 原子能科学技术, 2007, 41(3):339-342 doi: 10.3969/j.issn.1000-6931.2007.03.017Li Jihao, Sun Baogen, He Duohui, et al. Mapping of strip line beam position monitor at HLS LINAC based on logarithm ratio processing method[J]. Atomic Energy Science and Technology, 2007, 41(3): 339-342 doi: 10.3969/j.issn.1000-6931.2007.03.017 [10] 王贵诚, 王筠华, 蒋道满, 等. BPM 定标系统及其应用[J]. 核技术, 2003, 26(4):254-256 doi: 10.3321/j.issn:0253-3219.2003.04.002Wang Guicheng, Wang Junhua, Jiang Daoman, et al. A BPM calibration system and its application[J]. Nuclear Techniques, 2003, 26(4): 254-256 doi: 10.3321/j.issn:0253-3219.2003.04.002 [11] 何小中, 庞健, 李勤, 等. 束流模拟装置的阻抗对标定结果的影响[J]. 强激光与粒子束, 2014, 26:035104 doi: 10.3788/HPLPB20142603.35104He Xiaozhong, Pang Jian, Li Qin, et al. Influence of beam test stand’s impedance on calibration results[J]. High Power Laser and Particle Beams, 2014, 26: 035104 doi: 10.3788/HPLPB20142603.35104 [12] Shokair I R. Measuring axially varying beam position using B-dot monitors[J]. Review of Scientific Instruments, 1989, 60(9): 2969-2974. doi: 10.1063/1.1140637 [13] Ekdahl C A. Fourier-analyzing coil arrays for pulsed relativistic electron beam experiments[J]. Review of Scientific Instruments, 1984, 55(8): 1221-1228. doi: 10.1063/1.1137926 [14] Carlson R L, Ridlon R N, Stout L E. Multigigahertz beam current and position monitor for relativistic electron beams[J]. Review of Scientific Instruments, 1986, 57(10): 2471-2474. doi: 10.1063/1.1139095 [15] Rienstra W W, Haworth M D. An exact analysis for beam centroid position monitors used in pulsed intense relativistic electron-beam experiments[J]. Review of Scientific Instruments, 1991, 62(10): 2363-2367. doi: 10.1063/1.1142246 -
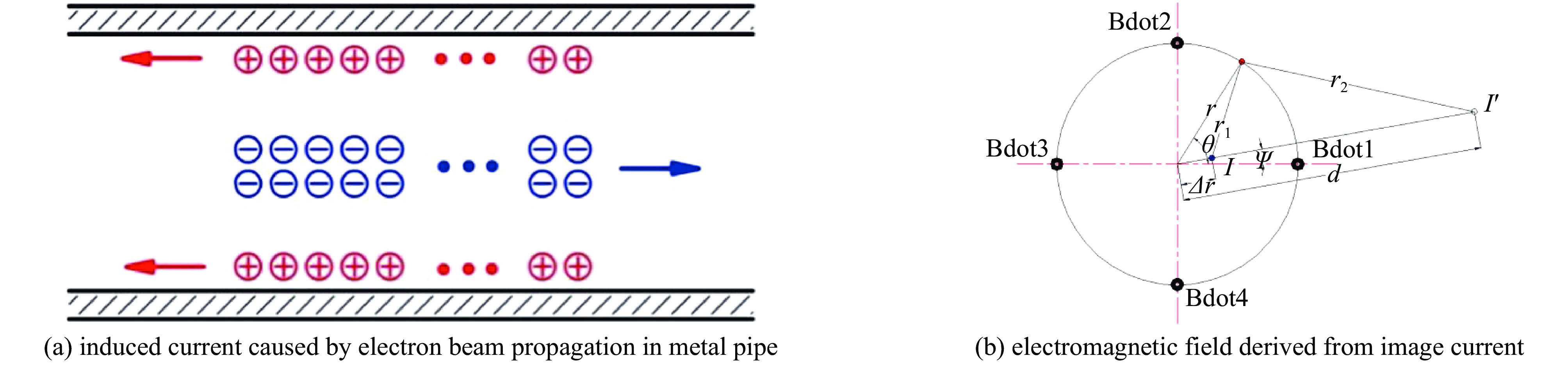
下载:
点击查看大图
计量
- 文章访问数: 590
- HTML全文浏览量: 230
- PDF下载量: 75
- 被引次数: 0
