Effect of load plasma disturbance on radiation temperature in Z-pinch dynamic hohlraum
-
摘要: 通过二维辐射流体力学模拟研究了Z箍缩动态黑腔负载等离子体撞击泡沫柱的动力学过程，探索了带扰动负载等离子体形状对黑腔内辐射温度的影响。结果表明，带有扰动的负载等离子体撞击泡沫后会产生Rayleigh-Taylor（RT）流体不稳定性，导致动态黑腔内的辐射在负载等离子体光薄区域发生漏失，使黑腔内辐射温度降低；负载等离子体扰动振幅越大、波长越大，辐射漏失越严重，同等动能加载条件下黑腔内辐射温度也越低。
-
关键词:
- Z箍缩 /
- 动态黑腔 /
- 等离子体扰动 /
- 辐射漏失 /
- Rayleigh-Taylor不稳定性
Abstract: The dynamic process of load plasma impacting on the foam cylinder was studied by two-dimensional radiation hydrodynamics simulation, and the influence of the shape of load plasma with disturbance on the radiation temperature in dynamic hohlraum was explored. The results show that Rayleigh-Taylor fluid instability will be generated after the disturbed load plasma impacting on the foam, and the development of RT instability will lead to the radiation leakage in the light-thin region of the load plasma, which will reduce the radiation temperature in the dynamic hohlraum. The larger the amplitude and the wavelength of disturbance in the load plasma, the more serious radiation leakage occurs, and the lower the radiation temperature will be in the dynamic hohlraum under the same kinetic energy loading condition.-
Key words:
- Z-pinch /
- dynamic hohlraum /
- plasma disturbance /
- radiation leakage /
- Rayleigh-Taylor instability
-
图 1 负载等离子体撞击泡沫模拟示意图
Figure 1. Schematic diagram of simulation of loaded plasma impinging on foam
图 2 t =3 ns时刻，高度z=0.3 cm处的压强(p)和辐射温度(Tr)的径向分布图
Figure 2. Radial distribution diagram of pressure (p) and radiation temperature (Tr) at t =3 ns and z=0.3 cm
图 3 z=0.3 cm、r=0.2 cm处动态黑腔内辐射温度(Tr)演化图
Figure 3. Evolution diagram of radiation temperature (Tr) in dynamic hohlraum at z= 0.3 cm and r= 0.2 cm
图 4 W等离子体撞击泡沫柱后不同时刻辐射温度(K)分布云图
Figure 4. Distribution cloud diagram of radiation temperature (K) at different time (t) after W plasma impinging on foam column
图 5 在t =4.5 ns时刻，高度z=0.3 cm处压强和密度径向分布
Figure 5. Radial distribution of pressure and density at time t =4.5 ns and height z=0.3 cm)
图 6 带扰动的负载撞击泡沫模拟示意图
Figure 6. Schematic diagram of load plasma with disturbance impacting foam
图 7 负载上不同扰动振幅下动态黑腔内的辐射温度 (Tr)演化
Figure 7. Radiation temperature (Tr) evolution in a dynamic hohlraum under different perturbation amplitudes on load
图 8 t=5 ns时刻不同初始扰动振幅(A)下密度分布云图
Figure 8. Cloud image of density distribution under different initial disturbance amplitudes (A) at time t=5 ns
图 9 t=5 ns时刻不同初始扰动振幅(A)下辐射温度 (Tr) 分布云图
Figure 9. Radiative temperature (Tr) distribution cloud at time t=5 ns with different initial disturbance amplitudes
图 10 负载上不同扰动波长(
$ \lambda $ )下动态黑腔辐射温度演化(r=0.1 cm)Figure 10. Radiation temperature evolution of dynamic hohlraum under different disturbance wavelengths (
$ \lambda $ ) on load
图 11 波长分别为0.2 cm和0.1 cm不同时刻下密度云图
Figure 11. Density contour at different time under disturbance wavelengths
$\lambda {\text{ = }}0.2$ cm and$\lambda {\text{ = }}0.1$ cm on load -
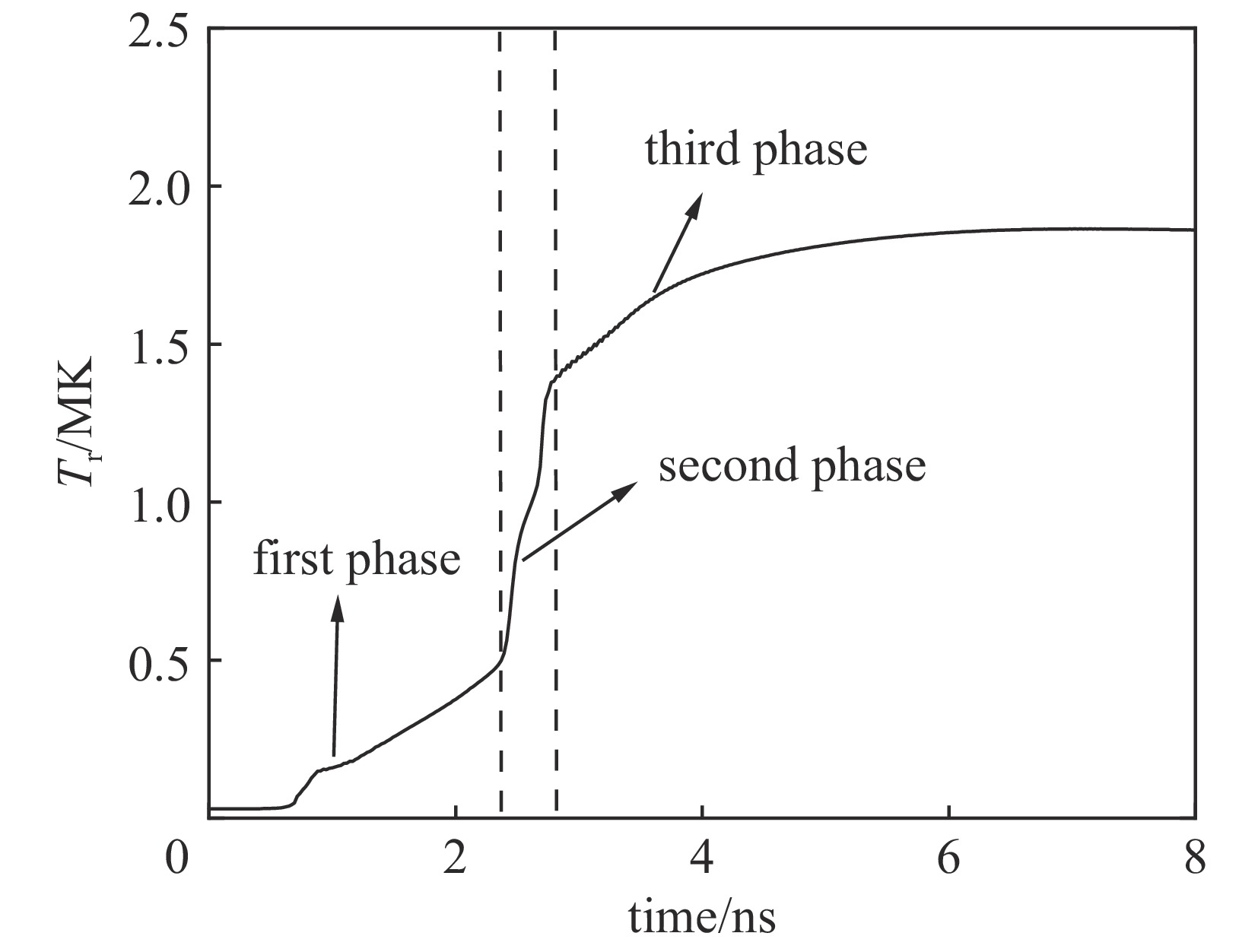
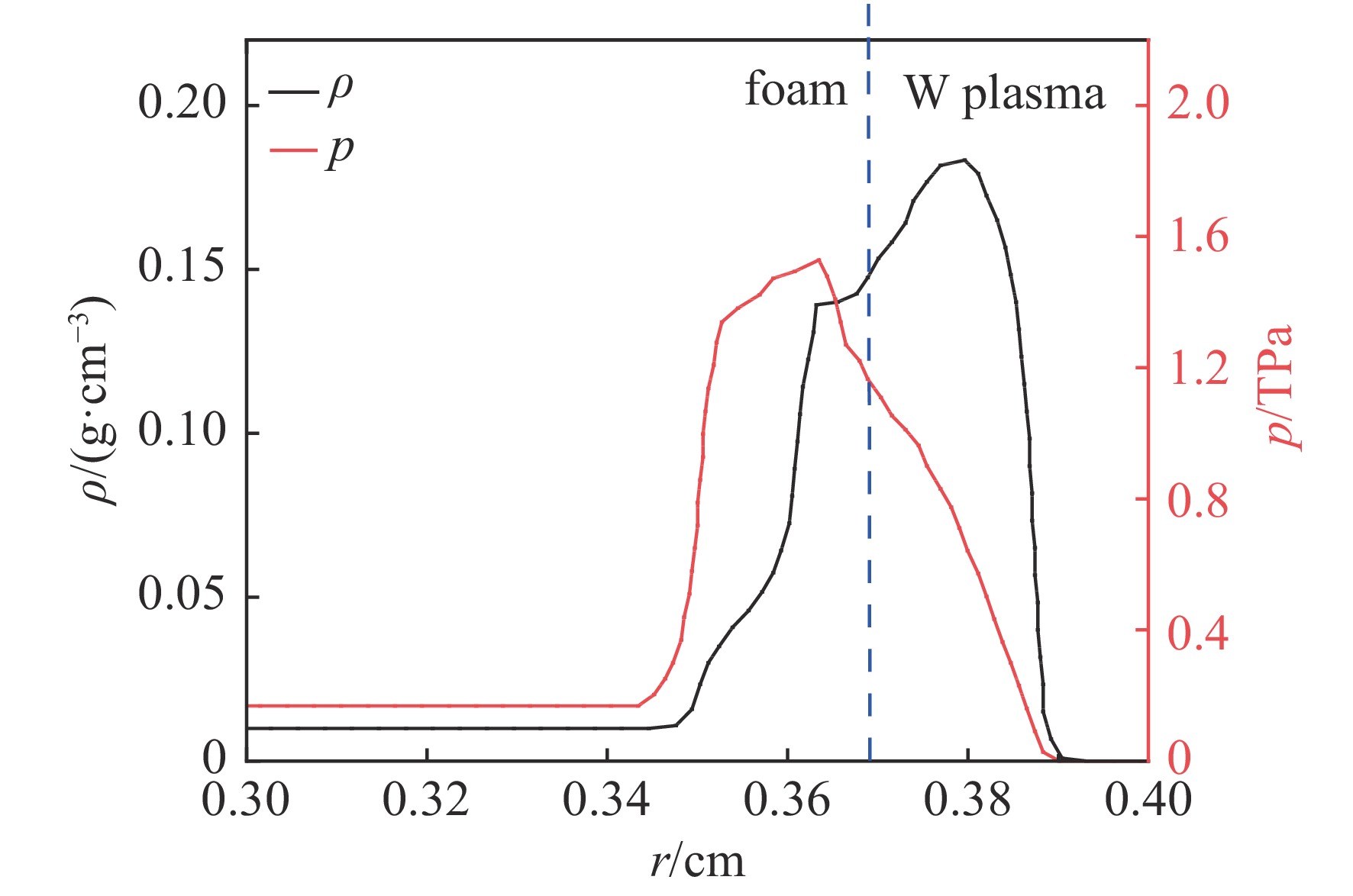
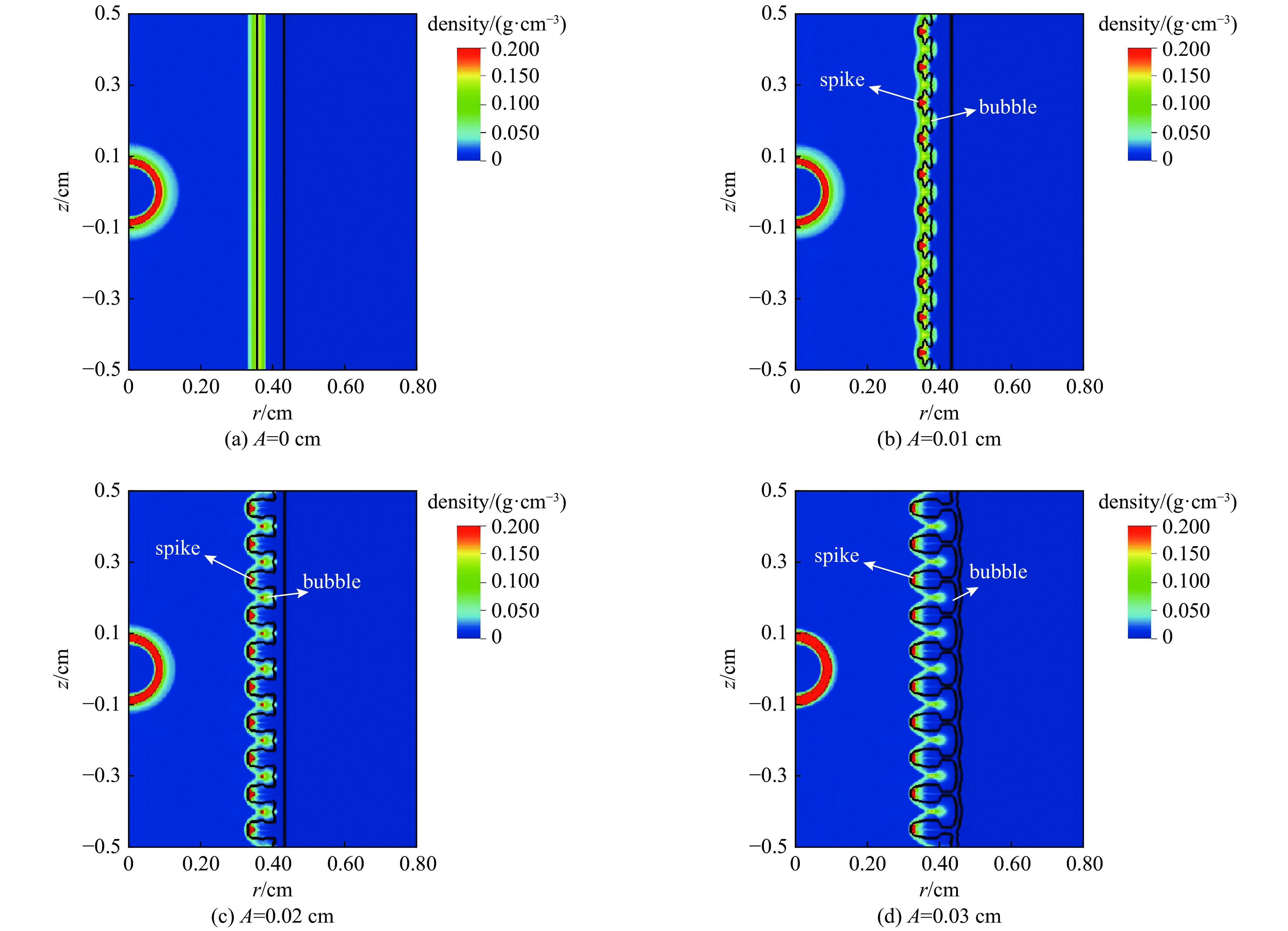
[1] 杜祥琬, 叶奇蓁, 徐銤, 等. 核能技术方向研究及发展路线图[J]. 中国工程科学, 2018, 20(3):17-24Du Xiangwan, Ye Qizhen, Xu Mi, et al. Research on technology directions and development roadmap of nuclear energy[J]. Strategic Study of CAE, 2018, 20(3): 17-24 [2] 彭先觉, 王真. Z箍缩驱动聚变-裂变混合能源堆总体概念研究[J]. 强激光与粒子束, 2014, 26:090201 doi: 10.3788/HPLPB20142609.90201Peng Xianjue, Wang Zhen. Conceptual research on Z-pinch driven fusion-fission hybrid reactor[J]. High Power Laser and Particle Beams, 2014, 26: 090201 doi: 10.3788/HPLPB20142609.90201 [3] 彭先觉, 刘成安, 师学明. 核能未来与Z箍缩驱动聚变裂变混合堆[M]. 北京: 国防工业出版社, 2019Peng Xianjue, Liu Cheng’an, Shi Xueming. Nuclear energy future and Z-pinch driven fusion fission hybrid reactor[M]. Beijing: National Defense Industry Press, 2019 [4] Slutz S A, Bailey J E, Chandler G A, et al. Dynamic hohlraum driven inertial fusion capsules[J]. Physics of Plasmas, 2003, 10(5): 1875-1882. doi: 10.1063/1.1565117 [5] Slutz S A, Peterson K J, Vesey R A, et al. Integrated two-dimensional simulations of dynamic hohlraum driven inertial fusion capsule implosions[J]. Physics of Plasmas, 2006, 13: 102701. doi: 10.1063/1.2354587 [6] Sanford T W L, Lemke R W, Mock R C, et al. Dynamics and characteristics of a 215-eV dynamic-hohlraum X-ray source on Z[J]. Physics of Plasmas, 2002, 9(8): 3573-3594. doi: 10.1063/1.1489676 [7] Bennett G R, Cuneo M E, Vesey R A, et al. Symmetric inertial-confinement-fusion-capsule implosions in a double-Z-pinch-driven hohlraum[J]. Physical Review Letters, 2002, 89: 245002. doi: 10.1103/PhysRevLett.89.245002 [8] Sanford T W L, Olson R E, Mock R C, et al. Dynamics of a Z-pinch X-ray source for heating inertial-confinement-fusion relevant hohlraums to 120–160 eV[J]. Physics of Plasmas, 2000, 7(11): 4669-4682. doi: 10.1063/1.1316087 [9] Rochau G A, Bailey J E, Chandler G A, et al. High performance capsule implosions driven by the Z-pinch dynamic hohlraum[J]. Plasma Physics and Controlled Fusion, 2007, 49(12B): B591-B600. doi: 10.1088/0741-3335/49/12B/S55 [10] 宁成, 丰志兴, 薛创. Z箍缩驱动动态黑腔中的基本能量转移特征. 物理学报, 2014, 63(12): 125208Ning Cheng, Feng Zhixing, Xuechuang. Basic characteristics of kinetic energy transfer in the dynamic hohlraums of Z-pinch. Acta Physica Sinica , 2014, 63(12): 125208. [11] 丁宁, 邬吉明, 戴自换, 等. Z箍缩内爆的MARED程序数值模拟分析[J]. 物理学报, 2010, 59(12):8707-8716 doi: 10.7498/aps.59.8707Ding Ning, Wu Jiming, Dai Zihuan, et al. Numerical simulation analysis of Z-pinch implosion using MARED code[J]. Acta Physica Sinica, 2010, 59(12): 8707-8716 doi: 10.7498/aps.59.8707 [12] 肖德龙, 孙顺凯, 薛创, 等. Z箍缩动态黑腔形成过程和关键影响因素数值模拟研究[J]. 物理学报, 2015, 64:235203 doi: 10.7498/aps.64.235203Xiao Delong, Sun Shunkai, Xue Chuang, et al. Numerical studies on the formation process of Z-pinch dynamic hohlruams and key issues of optimizing dynamic hohlraum radiation[J]. Acta Physica Sinica, 2015, 64: 235203 doi: 10.7498/aps.64.235203 [13] 肖德龙, 戴自换, 孙顺凯, 等. Z箍缩动态黑腔驱动靶丸内爆动力学[J]. 物理学报, 2018, 67:025203 doi: 10.7498/aps.67.20171640Xiao Delong, Dai Zihuan, Sun Shunkai, et al. Numerical studies on dynamics of Z-pinch dynamic hohlraum driven target implosion[J]. Acta Physica Sinica, 2018, 67: 025203 doi: 10.7498/aps.67.20171640 [14] 何开辉, 冯开明, 李强, 等. 金属丝阵列Z箍缩装置中的瑞利-泰勒不稳定性[J]. 核聚变与等离子体物理, 2000, 20(4):241-245 doi: 10.3969/j.issn.0254-6086.2000.04.010He Kaihui, Feng Kaiming, Li Qiang, et al. Preliminary study of Rayleigh-Taylor instability in wire-array Z-pinch[J]. Nuclear Fusion and Plasma Physics, 2000, 20(4): 241-245 doi: 10.3969/j.issn.0254-6086.2000.04.010 [15] Shumlak U, Roderick N F. Mitigation of the Rayleigh–Taylor instability by sheared axial flows[J]. Physics of Plasmas, 1998, 5(6): 2384-2389. doi: 10.1063/1.872913 [16] 张扬, 丁宁. 轴向流对Z箍缩等离子体稳定性的影响[J]. 物理学报, 2006, 55(5):2333-2339 doi: 10.3321/j.issn:1000-3290.2006.05.037Zhang Yang, Ding Ning. The effect of axial flow on the stability in the Z-pinch[J]. Acta Physica Sinica, 2006, 55(5): 2333-2339 doi: 10.3321/j.issn:1000-3290.2006.05.037 [17] 段耀勇, 郭永辉, 王文生, 等. Z箍缩等离子体不稳定性的数值研究[J]. 物理学报, 2004, 53(10):3429-3434 doi: 10.3321/j.issn:1000-3290.2004.10.036Duan Yaoyong, Guo Yonghui, Wang Wensheng, et al. Numerical investigations of Z-pinch plasma instabilities[J]. Acta Physica Sinica, 2004, 53(10): 3429-3434 doi: 10.3321/j.issn:1000-3290.2004.10.036 [18] Wang Guanqiong, Xiao Delong, Dan Jiakun, et al. Preliminary investigation on electrothermal instabilities in early phases of cylindrical foil implosions on primary test stand facility[J]. Chinese Physics B, 2019, 28: 025203. doi: 10.1088/1674-1056/28/2/025203 [19] 陈忠旺, 宁成. 基于MULTI2D-Z程序的Z箍缩动态黑腔形成过程模拟[J]. 物理学报, 2017, 66:125202 doi: 10.7498/aps.66.125202Chen Zhongwang, Ning Cheng. Simulation of forming process of Z-pinch dynamic hohlraum based on the program MULTI2D-Z[J]. Acta Physica Sinica, 2017, 66: 125202 doi: 10.7498/aps.66.125202 [20] Brownell J H, Bowers R L, McLenithan K D, et al. Radiation environments produced by plasma Z-pinch stagnation on central targets[J]. Physics of Plasmas, 1998, 5(5): 2071-2080. doi: 10.1063/1.872879 [21] 徐彬彬. Z箍缩动态黑腔内辐射温度与均匀性以及烧蚀层界面不稳定性研究[D]. 长沙: 国防科技大学, 2017Xu Binbin. Research on the radiation temperature and radiation uniformity in Z-pinch dynamic hohlraum and the fluid instability in ablator[D]. Changsha: National University of Defense Technology, 2017 [22] Fryxell B, Olson K, Ricker P, et al. FLASH: an adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes[J]. The Astrophysical Journal Supplement Series, 2000, 131(1): 273-334. doi: 10.1086/317361 [23] 龙城德, 赵斌, 袁鹏, 等. 小焦斑纳秒激光烧蚀铝平面靶的数值研究[J]. 强激光与粒子束, 2014, 26:102005 doi: 10.11884/HPLPB201426.102005Long Chengde, Zhao Bin, Yuan Peng, et al. Simulation of expansion of aluminum plasmas produced by a small focal spot nanosecond laser irradiation[J]. High Power Laser and Particle Beams, 2014, 26: 102005 doi: 10.11884/HPLPB201426.102005 [24] Tzeferacos P, Fatenejad M, Flocke N, et al. FLASH magnetohydrodynamic simulations of shock-generated magnetic field experiments[J]. High Energy Density Physics, 2012, 8(4): 322-328. doi: 10.1016/j.hedp.2012.08.001 [25] 孙伟, 吕冲, 雷柱, 等. 磁场对激光驱动Rayleigh-Taylor不稳定性影响的数值研究[J]. 物理学报, 2022, 71:154701 doi: 10.7498/aps.71.20220362Sun Wei, Lü Chong, Lei Zhu, et al. Numerical study of effect of magnetic field on laser-driven Rayleigh-Taylor instability[J]. Acta Physica Sinica, 2022, 71: 154701 doi: 10.7498/aps.71.20220362 [26] Faik S, Tauschwitz A, Iosilevskiy I. The equation of state package FEOS for high energy density matter[J]. Computer Physics Communications, 2018, 227: 117-125. doi: 10.1016/j.cpc.2018.01.008 [27] Kemp A J, Meyer-ter-Vehn J. An equation of state code for hot dense matter, based on the QEOS description[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 1998, 415(3): 674-676. doi: 10.1016/S0168-9002(98)00446-X [28] 赵凯歌, 薛创, 王立锋, 等. 经典瑞利-泰勒不稳定性界面变形演化的改进型薄层模型[J]. 物理学报, 2018, 67:094701 doi: 10.7498/aps.67.20172613Zhao Kaige, Xue Chuang, Wang Lifeng, et al. Improved thin layer model of classical Rayleigh-Taylor instability for the deformation of interface[J]. Acta Physica Sinica, 2018, 67: 094701 doi: 10.7498/aps.67.20172613 -
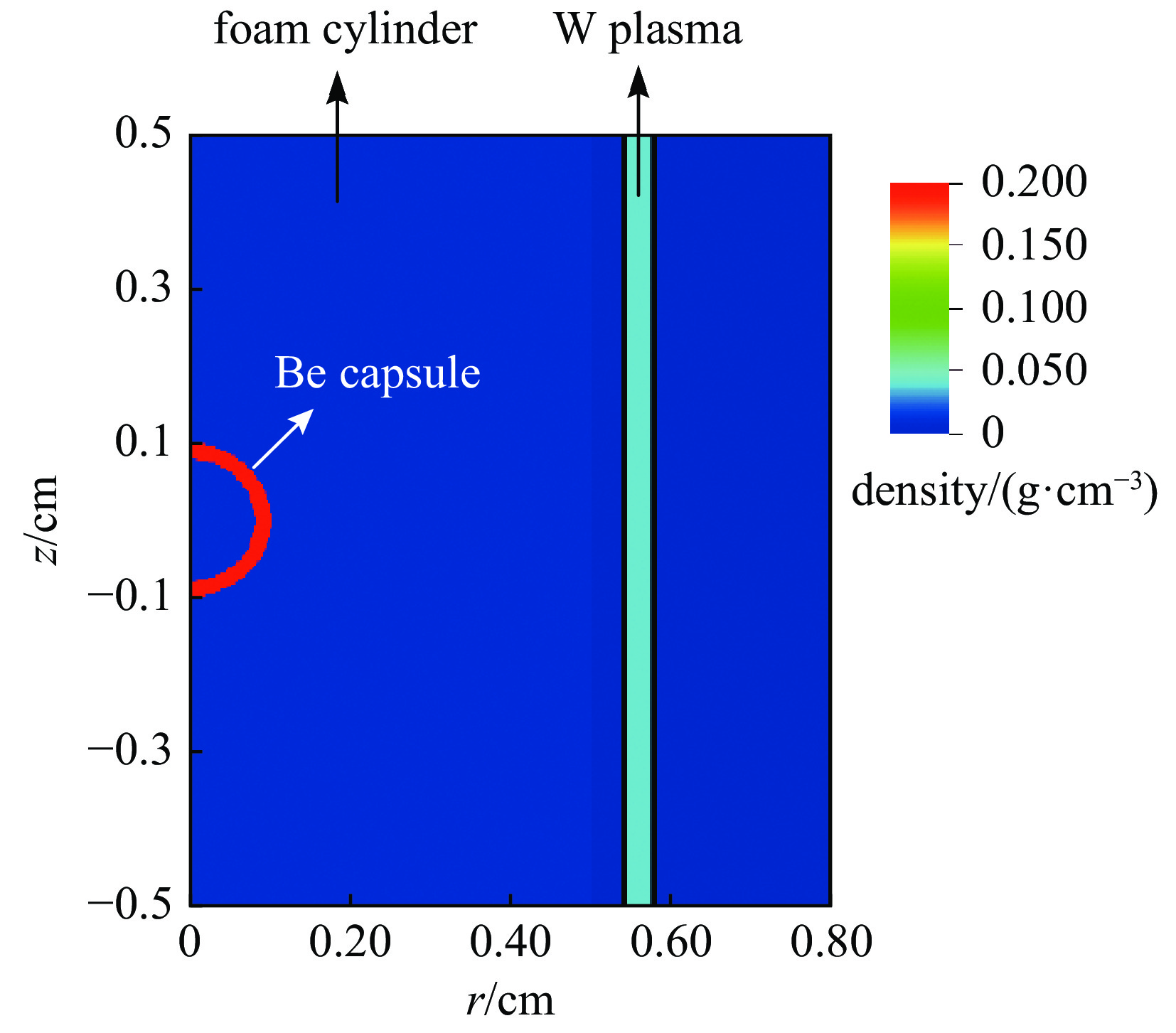
下载:
点击查看大图
计量
- 文章访问数: 516
- HTML全文浏览量: 236
- PDF下载量: 68
- 被引次数: 0
